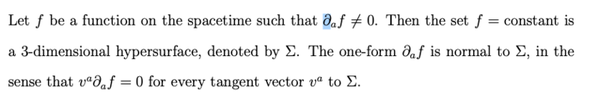A Hypersurface Definition Confusion in General Relativity

[tm33333]

In my notes on general relativity, hypersurfaces are defined as in the image. What confuses me is that if f=constant, surely the partial differential is going to be zero? I'm not sure if I'm missing something, but surely the function can't be equal to a constant and its partial differential be non-zero?

thanks.

 

[Ibix]

It's requiring that $\partial_af$ be non-zero everywhere, then saying the subset of points with the same value of $f$ define a hypersurface. Analogously, you can define a function $f(x,y)$ on a two dimensional Euclidean plane and the lines of constant $f$ are the contour lines (1d analogues to 3d hypersurfaces). The gradient on a contour isn't zero, it is perpendicular to the contour line.

(Note that geographical contour lines can close, but a closed contour line encloses at least one point where the gradient is zero, so the definition of a hypersurface excludes this possibility).

 

[Orodruin]

Well, the requirement that $\partial_a f=0$ everywhere is a bit strict. It is sufficient that it is non-zero at the hypersurface being described by the particular constant. (Although you will need the full requirement if you intend to make a foliation of the manifold.)

As an example, consider the sphere in standard Euclidean space with $f = x^2 + y^2 + z^2$. For $R>0$, $f = R^2$ defines a sphere of radius $R$, which is a level surface of $f$ in $\mathbb R^3$.

 

[tm33333]

Thank you both. That definitely clarifies things!

 

[PeterDonis]

Moderator's note: Thread title edited to be more descriptive of the specific question.

 

[robphy]

Thank you both. That definitely clarifies things!

I guess you can say that they broke it down for you.