If f(x)=(e^x+e^-x)/2, what is the inverse function?

[Darkmisc]

Homework Statement

If f(x)=(e^x+e^-x)/2, what is the inverse function?

Relevant Equations

f(x)=(e^x+e^-x)/2

Hi everyone

This is the solution for the problem.

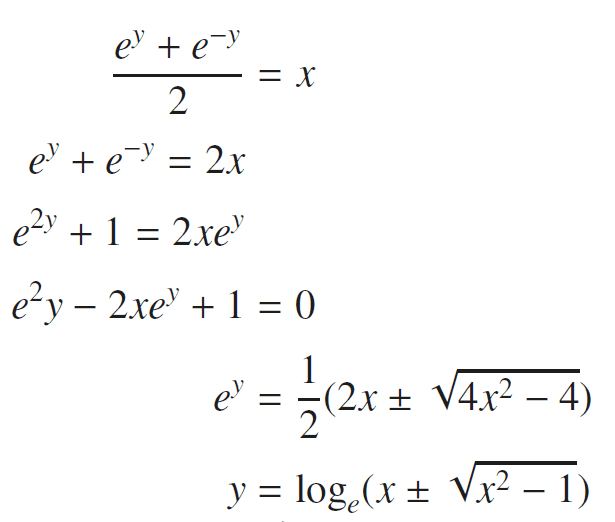
I don't understand how they got from

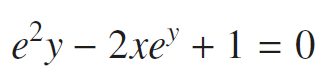
To

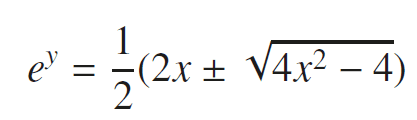
This was my attempt at a solution

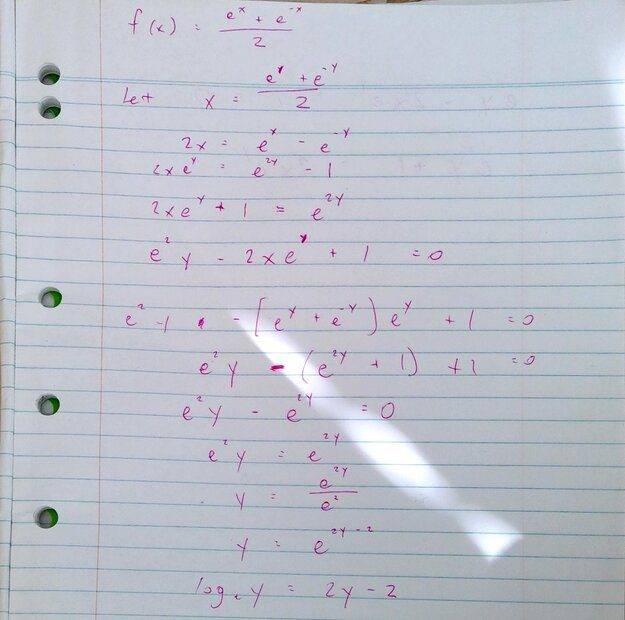
I can't seem to get rid of one of the y terms and am left with one on each side.

Could someone explain the solution to me please?

Thanks

 

[FactChecker]

View attachment 302970

This line has a mistake. The first y is in the exponent.

To
View attachment 302971

This is just using the quadratic formula to solve for $e^y$.

 

[nuuskur]

$e^x + e^{-x}$ is not injective in $\mathbb R$ (even function). You should assume either $x<0$ or $x>0$.

 

[mathwonk]

note: x = (1/2)(e^y + e^-y) = cos(iy). so the inverse is -i.arccos(x).

 

[pasmith]

note: x = (1/2)(e^y + e^-y) = cos(iy). so the inverse is -i.arccos(x).

We call that function "cosh", so the inverse is $\operatorname{arccosh}(x)$.

 

[WWGD]

We call that function "cosh", so the inverse is $\operatorname{arccosh}(x)$.

Isn't it just a local inverse, as @nuuskur pointed out?

 

[Delta2]

er sorry $$\operatorname{arccosh}(x)=-i\arccos(x)$$?

Btw there is a silly typo that was spotted successfully by @FactChecker the quadratic with respect to $e^y$ is $(e^y)^2-2xe^y+1=0$ for which you can set $z=e^y$ solve it for z(x) as a normal quadratic and then take $$e^y=z(x)\Rightarrow y=\ln z(x)$$.

 

[WWGD]

er sorry $$\operatorname{arccosh}(x)=-i\arccos(x)$$?

Btw there is a silly typo that was spotted successfully by @FactChecker the quadratic with respect to $e^y$ is $(e^y)^2-2xe^y+1=0$ for which you can set $z=e^y$ solve it for z(x) as a normal quadratic and then take $$e^y=z(x)\Rightarrow y=\ln z(x)$$.

With the caveats that $z(x) >0$, and, for well definedness, its an injection, I guess.

 

[vela]

$$\operatorname{arccosh}(x)=-i\arccos(x)$$?

You're probably confused because you're thinking of cosine defined for reals. If you consider the cosine function defined for complex numbers, it makes sense.

With the caveats that $z(x) >0$, and, for well definedness, its an injection, I guess.

If $y$ is real, then $e^y>0$.

Note that the quadratic has two solutions, $y_+$ and $y_-$. To make the inverse a function, we arbitrarily choose the positive root and map $x$ to $y_+$.

It's not obvious, but you can show that $y_- = -y_+$.

 

[Orodruin]

Am I the only one reacting on the use of ”arccosh” instead of the standard ”arcosh”?

 

[FactChecker]

It's not obvious, but you can show that $y_- = -y_+$.

Is that true? I don't see it.

 

[vela]

Hint: $(x + \sqrt{x^2-1})(x-\sqrt{x^2-1})=1$.

 

[vela]

Am I the only one reacting on the use of ”arccosh” instead of the standard ”arcosh”?

I think the "arc" notation is pretty common. Mathematica, for example, calls the function ArcCosh.

In fact, until you pointed it out, I didn't know "arcosh" was the standard way to write it.

 

[Orodruin]

Mathematica, for example, calls the function ArcCosh.

Mathematica is then not up to ISO 80000-2 standard.

But yes, it is a fairly common mistake but arccosh would be a misnomer as the function does not relate to arc length but to area (unless measuring in Minkowski geometry….)

 

[WWGD]

You're probably confused because you're thinking of cosine defined for reals. If you consider the cosine function defined for complex numbers, it makes sense.If $y$ is real, then $e^y>0$.

Note that the quadratic has two solutions, $y_+$ and $y_-$. To make the inverse a function, we arbitrarily choose the positive root and map $x$ to $y_+$.

It's not obvious, but you can show that $y_- = -y_+$.

Ah, I missed that result before log(z(x)).

 

[Delta2]

Hint: $(x + \sqrt{x^2-1})(x-\sqrt{x^2-1})=1$.

Ehm that is correct but all you can actually prove with this is that $y_{+}=\frac{1}{y_{-}}$.

Ah ok you mean the solutions to $e^y=z(x)$ or $e^y=\frac{1}{z(x)}$

 

[nuuskur]

For invertibility of $\cosh x$ (in $\mathbb R$), we usually mean
$$\cosh : [0,\infty) \to [1,\infty),\quad \cosh(x) := \frac{e^x+e^{-x}}{2}.$$
Putting
$$g : [1,\infty ) \to [0,\infty ),\quad g(x) := \ln (x+\sqrt{x^2-1})$$
one can verify that $g\circ \cosh$ and $\cosh \circ g$ are the identities. From $y_+y_- = 1$ it follows that $\ln y_- < 0$, so it couldn't be the correct choice in this case.

But it's completely fine to define $\cosh$ on the negative side. In that case, for the inverse, one also opts for $\ln y_-$.