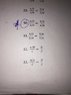Joshper14
- 2
- 0
Homework Statement
Revised by mentor:
Solve for x
$$\frac{\frac 1 2}{\frac 3 4 } = \frac{\frac 5 6 }{\frac x 8 } $$
Note to OP: This is $$\frac{\frac 1 2}{\frac 3 4 } = \frac{\frac 5 6 }{\frac x 8 } $$
Homework Equations
$$\frac{\frac{a}{x}}{\frac{c}{1}}$$
The Attempt at a Solution
I don't know how to post my workings but here's the answer I got
X= $$\frac{BCD}{E}$$
Last edited by a moderator: