JoeyF
- 13
- 0
- TL;DR Summary
- Having trouble forming a FBD to understand a latch mechanism I'm designing. See details below.
I apologize if this is the wrong area to post this in, I've never posted on thisforum before.
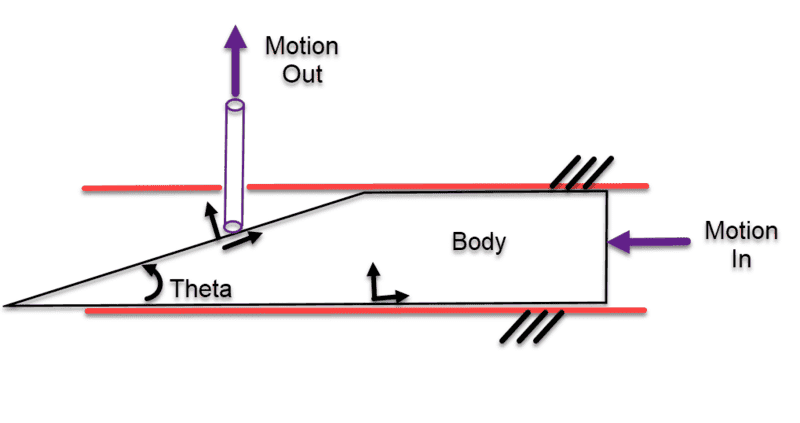
I'm trying to form a FBD of a mechanism that uses linear motion to actuate a pin in a transverse direction. I've attached the general idea in a picture where the pin is free to move up and down. In reality the pin is more of a spring, but I think it will be easier to model as a pin with a given weight so I can assume constant force in that direction. Also attached a more detailed FBD representing actual CAD.
I would like to know the relationship between the incline angle, and resultant push force required to move the body. When I plug my systems of equations into Wolframalpha, I get negative results for N2 and Fp, which indicates I am making wrong assumptions. I even tried a couple different coordinate systems with no luck. My hunch is that my assumption highlighted in red is incorrect.
This is my work so far. Thanks in advance!
General Idea:
FBD for Purple Body:
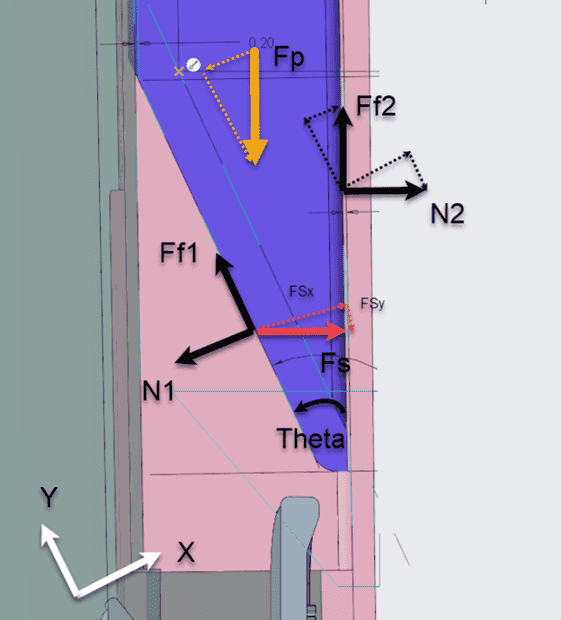
Assumptions:
Mu1 = Mu2 = 0.3
Fs = 17N
Unknown Variables:
Fp =? (Plunger Push Force)
N2 =? (normal force from cap)
Declaration of Equations:
Fsx = Fs*cos(theta)
N1 = Fsx
Ff1 = N1*Mu1 …. N1 = Ff1/Mu
Fsy = Fs*sin(theta)
Ff2 = N2*Mu2Summation of Forces:
Sum of Forces in X = N1 – Fsx + N2*cos(theta) - Ff2*sin(theta) + Fp*sin(theta) --------->
0 = 17*cos(theta) – 17*cos(theta) + N2*cos(theta) - N2*0.3*sin(theta) + Fp*sin(theta)
Sum of Forces in Y = Ff1 – Fsy – N2*sin(theta) + Ff2*cos(theta) – Fp*cos(theta) --------->
0 = 17*cos(theta)*0.3 – 17*sin(theta) + N2*sin(theta) + N2*0.3*cos(theta) - Fp*cos(theta)
I'm trying to form a FBD of a mechanism that uses linear motion to actuate a pin in a transverse direction. I've attached the general idea in a picture where the pin is free to move up and down. In reality the pin is more of a spring, but I think it will be easier to model as a pin with a given weight so I can assume constant force in that direction. Also attached a more detailed FBD representing actual CAD.
I would like to know the relationship between the incline angle, and resultant push force required to move the body. When I plug my systems of equations into Wolframalpha, I get negative results for N2 and Fp, which indicates I am making wrong assumptions. I even tried a couple different coordinate systems with no luck. My hunch is that my assumption highlighted in red is incorrect.
This is my work so far. Thanks in advance!
General Idea:
FBD for Purple Body:
Assumptions:
- Frictionless Top surface of purple Plunger (green surface)
- Normal Force in X direction is equal to Fs (Fsx = N1)
Mu1 = Mu2 = 0.3
Fs = 17N
Unknown Variables:
Fp =? (Plunger Push Force)
N2 =? (normal force from cap)
Declaration of Equations:
Fsx = Fs*cos(theta)
N1 = Fsx
Ff1 = N1*Mu1 …. N1 = Ff1/Mu
Fsy = Fs*sin(theta)
Ff2 = N2*Mu2Summation of Forces:
Sum of Forces in X = N1 – Fsx + N2*cos(theta) - Ff2*sin(theta) + Fp*sin(theta) --------->
0 = 17*cos(theta) – 17*cos(theta) + N2*cos(theta) - N2*0.3*sin(theta) + Fp*sin(theta)
Sum of Forces in Y = Ff1 – Fsy – N2*sin(theta) + Ff2*cos(theta) – Fp*cos(theta) --------->
0 = 17*cos(theta)*0.3 – 17*sin(theta) + N2*sin(theta) + N2*0.3*cos(theta) - Fp*cos(theta)