Inequality question -- Need help getting started...

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this,

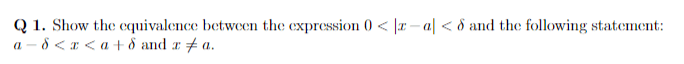
I am confused how to show that they are equivalent. Can some please give me some guidance?

Many thanks!

 

[FactChecker]

What is always the first step when absolute values are involved? Two cases for |x-a|, depending on the sign of x-a.
Where can you go from there?

 

[member 731016]

What is always the first step when absolute values are involved? Two cases for |x-a|, depending on the sign of x-a.
Where can you go from there?

Thanks for your reply @FactChecker!

First case is

-(x - a)

Second case is

x - a

 

[FactChecker]

Right. Now you need to show some work using that.

 

[member 731016]

Right. Now you need to show some work using that.

Thanks @FactChecker!

$0 < -(x - a) < \delta$
$0 < x - a <\delta$

Many thanks!

 

[member 731016]

Thanks @FactChecker!

$0 < -(x - a) < \delta$
$0 < x - a <\delta$

Many thanks!

Nevermind, I understand now. It seems so strange that you can multiply all three sides of an equality by the same number. I don't know what this property is called thought.

 

[Mark44]

I am confused how to show that they are equivalent. Can some please give me some guidance?

For the continued inequality $0 < |x - a| < \delta$, it's helpful to draw a sketch or two of the number line with a in an arbitrary position. x will then have to be somewhere inside a band of width $2\delta$ around a, but excluding a itself.

Nevermind, I understand now. It seems so strange that you can multiply all three sides of an equality by the same number. I don't know what this property is called thought.

The statement you started with is not an equation -- it's an inequality. There is a property of equations that you can multiply both sides of an equation by any nonzero number to get a new, equivalent equation. This idea can be extended to a continued equation.

There is a similar property for inequalities, but with a twist. You can multiply both sides of an inequality by a positive number to get a new, equivalent inequality. This also can be extended to continued inequalities. The twist is that if you multiply both sides by a negative number, the direction of the inequality must change.

Yet again, the very large gaps in your mathematical background are causing you to spend a lot of time merely trying to understand what would be immediately obvious to someone who didn't have these gaps.

 

[FactChecker]

Yet again, the very large gaps in your mathematical background are causing you to spend a lot of time merely trying to understand what would be immediately obvious to someone who didn't have these gaps.

Amen! Mathematics is very cumulative. Anything that you were taught earlier will be used over and over in what follows. It can be very beneficial to review earlier material until it becomes natural to you.