Integral ## \int _{ }^{ }\frac{1}{\sqrt{x^3+1}}dx ##

[Tapias5000]

Homework Statement

These types of problems have been a mystery to me.
According to wolfram this ends in the function $_2F1(a,b;c;z)$
but how?

Relevant Equations

$_2F1(a,b;c;z)=\sum _{n=0}^∞\frac{\left(a\right)_n\left(b\right)_n}{\left(c\right)_n}=1+\frac{abz}{c1!}+\frac{a\left(a+1\right)b\left(b+1\right)z^2}{c\left(c+1\right)2!}+...$

I also don't understand how to get the descending factorials for this hypergeometric series, I also know that there is another way to write it with gamma functions, but in any case how am I supposed to do this?
If I write it as a general term, wolfram will give me the result

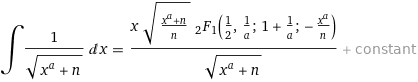
which leaves me even more puzzled since I do not understand where a, b and c are
Could you tell me where to start? or where you should keep looking for information.

 

[pasmith]

Set $I = \int 1/\sqrt{1 + x^a}\,dx$ and find $p(x)$ and $q(x)$ such that $$\frac{d^2I}{dx^2} + p(x)\frac{dI}{dx} + q(x)I = 0.$$ Then solve this ODE using Frobenius' Method to get a power series, which you then need to recognise as the power series of whatever Wolfram told you the integral is. Or recognise that setting $I(x) = xf(-x^a)$ leads to $f$ satisfying the hypergeometric differential equation,$$z(1-z)f'' + (c - (a + b + 1)z)f' - abf = 0.$$ (Note that the expression given by wolfram can be further simplified to $(x/\sqrt{n}){}_2F_1(\dots)$.)

 

[Tapias5000]

Set $I = \int 1/\sqrt{1 + x^a}\,dx$ and find $p(x)$ and $q(x)$ such that $$\frac{d^2I}{dx^2} + p(x)\frac{dI}{dx} + q(x)I = 0.$$ Then solve this ODE using Frobenius' Method to get a power series, which you then need to recognise as the power series of whatever Wolfram told you the integral is. Or recognise that setting $I(x) = xf(-x^a)$ leads to $f$ satisfying the hypergeometric differential equation,$$z(1-z)f'' + (c - (a + b + 1)z)f' - abf = 0.$$ (Note that the expression given by wolfram can be further simplified to $(x/\sqrt{n}){}_2F_1(\dots)$.)

How do I obtain p (x) and q (x) ?, I had done similar exercises but in that case I did it from the solution already given ...
oh i got to solve the edo
$\frac{d^2I}{dx^2}+\frac{dI}{dx}+I=0$
and then replace?

 

[Tapias5000]

How do I obtain p (x) and q (x) ?, I had done similar exercises but in that case I did it from the solution already given ...
oh i got to solve the edo
$\frac{d^2I}{dx^2}+\frac{dI}{dx}+I=0$
and then replace?

what I did was the following, even though I am sure this is incorrect.
$I=\frac{1}{\sqrt{1+x^a}}$

$\frac{dI}{dx}=-\frac{ax^{a-1}}{2\left(1+x^a\right)^{\frac{3}{2}}},\ \ \frac{d^2I}{dx^2}=-\frac{ax^{a-2}\left(-ax^a-2x^a+2a-2\right)}{4\left(x^a+1\right)^{\frac{5}{2}}}$

$\frac{d^2I}{dx^2}+p\left(x\right)\frac{dI}{dx}+q\left(x\right)I=0$

$-\frac{ax^{a-2}\left(-ax^a-2x^a+2a-2\right)}{4\left(x^a+1\right)^{\frac{5}{2}}}-p\left(x\right)\frac{ax^{a-1}}{2\left(1+x^a\right)^{\frac{3}{2}}}+q\left(x\right)\frac{1}{\sqrt{1+x^a}}=0$

$p\left(x\right)=\frac{-ax^a-2x^a+2a-2}{2\left(x^a+1\right)x}+q\left(x\right)\frac{2\left(1+x^a\right)}{ax^{a-1}}$

$-\frac{ax^{a-2}\left(-ax^a-2x^a+2a-2\right)}{4\left(x^a+1\right)^{\frac{5}{2}}}-\left(\frac{-ax^a-2x^a+2a-2}{2\left(x^a+1\right)x}+q\left(x\right)\frac{2\left(1+x^a\right)}{ax^{a-1}}\right)\frac{ax^{a-1}}{2\left(1+x^a\right)^{\frac{3}{2}}}+q\left(x\right)\frac{1}{\sqrt{1+x^a}}=0$

I doubt this is the way ...

 

[pasmith]

Hint: if $f = g(x)^\beta$ then $$\frac{df}{dx} = \beta g(x)^{\beta - 1} \frac{dg}{dx}= \left(\frac{\beta}{g(x)}\frac{dg}{dx}\right)f.$$

 

[Tapias5000]

Hint: if $f = g(x)^\beta$ then $$\frac{df}{dx} = \beta g(x)^{\beta - 1} \frac{dg}{dx}= \left(\frac{\beta}{g(x)}\frac{dg}{dx}\right)f.$$

Where did you get the last equation from?

$\left(\frac{\beta}{g(x)}\frac{dg}{dx}\right)f$

 

[Tapias5000]

@pasmith I tried another approach obtaining the following, I do not know if it is correct

\begin{array}{l}\int_{ }^{ }\frac{1}{\sqrt{x^3+1}}dx\\

\int_{ }^{ }\left(x^3+1\right)^{-\frac{1}{2}}dx\\

\left(1+u\right)^R\ \ \left[u=x^3,\ R=-\frac{1}{2}\right]\\

f\left(u\right)=\left(1+u\right)^R\\

f^{\prime}\left(u\right)=R\left(1+u\right)^{R-1}\\

f^{\prime\prime}\left(u\right)=R\left(R-1\right)\left(1+u\right)^{R-2}\\

f^{\prime\prime\prime}\left(u\right)=R\left(R-1\right)\left(R-2\right)\left(1+u\right)^{R-3}\\

f^{\prime\prime\prime\prime}\left(u\right)=R\left(R-1\right)\left(R-2\right)\left(R-3\right)\left(1+u\right)^{R-4}\\

f^n\left(u\right)=\left(R\right)_n\left(1+u\right)^{R-n}\ \ ,\ \left[R<0\right]\\

f\left(0\right)=1\\

f^{\prime}\left(0\right)=R\\

f^{\prime\prime}\left(0\right)=R\left(R-1\right)\\

f^{\prime\prime\prime}\left(0\right)=R\left(R-1\right)\left(R-2\right)\\

f^{\prime\prime\prime\prime}\left(u\right)=R\left(R-1\right)\left(R-2\right)\left(R-3\right)\\

f^n\left(0\right)=\left(R\right)_n\ \left[R<0\right]\\

\frac{f\left(0\right)}{0!}+\frac{f^{\prime}\left(0\right)u}{1!}+\frac{f^{\prime\prime}\left(0\right)u^2}{2!}+\frac{f^{\prime\prime\prime}\left(0\right)u^3}{3!}+\frac{f^{\prime\prime\prime\prime}\left(0\right)u^4}{4!}+...\frac{f^n\left(0\right)u^n}{n!}\\

1+\frac{Rx}{1!}+\frac{R\left(R-1\right)x^2}{2!}+\frac{R\left(R-1\right)\left(R-2\right)x^3}{3!}+\frac{R\left(R-1\right)\left(R-2\right)\left(R-3\right)x^4}{4!}+...\frac{\left(R\right)_nu^n}{n!}\ \ \left[u=x^3,\ R=-\frac{1}{2}\right]\\

1-\frac{x}{2\cdot1!}+\frac{3x^2}{2^2\cdot2!}-\frac{1\left(3\right)\left(5\right)x^3}{2^33!}+\frac{1\left(3\right)\left(5\right)\left(7\right)x^4}{2^44!}\ +...\frac{-\left(\frac{1}{2}\right)_nx^{3n}}{n!}\\

\sum_{n=0}^{\infty}\frac{\left(R\right)_nu^n}{n!}\ \ \left[u=x^3,\ R=-\frac{1}{2}\right]\\

\int_{ }^{ }\sum_{n=0}^{\infty}\frac{-\left(\frac{1}{2}\right)_nx^{3n}}{n!}dx...\ ?\end{array}

 

[Tapias5000]

This is what I have been able to advance, I am concerned if the declining factor of 4/3 is actually correct ...