ineedhelpnow
- 649
- 0
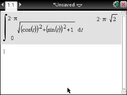
find the length of an arc of a helix r(t)=(sint,cost,t) from the point (0,2,0) to (0,5,2pi)
would the interval when integrating be from 0 to 2pi because t in the case is (z=t)? please say yes. please say yes.
would the interval when integrating be from 0 to 2pi because t in the case is (z=t)? please say yes. please say yes.
Last edited: