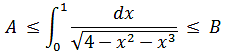Interval of the Riemann integral value

In summary, the conversation discusses finding an interval for a Riemann integral and suggests using the function $\tfrac1{\sqrt{4-x^2-x^3}}$, which is known to increase on the interval $0\leqslant x\leqslant 1$, to estimate values for $A$ and $B$.
  • #1
goody1
16
0
Hello everyone, I have to find an interval of this Riemann integral. Does anybody know the easiest way how to do it? I think we need to do something with denominator, enlarge it somehow. My another guess is the integral is always larger than 0 (A=0) because the whole function is still larger than 0 on interval from 0 to 1. Thank you in advance.
 

Attachments

  • integral.png
    integral.png
    1 KB · Views: 83
Physics news on Phys.org
  • #2
The function $\tfrac1{\sqrt{4-x^2-x^3}}$ increases on the interval $0\leqslant x\leqslant 1$. The minimum value occurs when $x=0$, and the maximum at $x=1$. You can use that to get estimates for $A$ and $B$.
 
  • #3
Opalg said:
The function $\tfrac1{\sqrt{4-x^2-x^3}}$ increases on the interval $0\leqslant x\leqslant 1$. The minimum value occurs when $x=0$, and the maximum at $x=1$. You can use that to get estimates for $A$ and $B$.
I tried this. Is that corect solution?
 

Attachments

  • inn.png
    inn.png
    1.2 KB · Views: 99
  • #4
goody said:
I tried this. Is that corect solution?
Yes, that is what I had in mind. :)
 

FAQ: Interval of the Riemann integral value

What is the interval of the Riemann integral value?

The interval of the Riemann integral value refers to the range of values that the Riemann integral can take on. It is typically denoted by [a, b], where a and b are the lower and upper bounds of the interval, respectively.

How is the interval of the Riemann integral value determined?

The interval of the Riemann integral value is determined by the limits of integration, which represent the starting and ending points of the function being integrated. These limits can be set by the user or may be given in the problem.

What is the significance of the interval of the Riemann integral value?

The interval of the Riemann integral value is important because it represents the area under the curve of a function within a specific range. This area can have physical or mathematical significance and can be used to solve various problems in calculus and other fields of science.

Can the interval of the Riemann integral value be infinite?

Yes, the interval of the Riemann integral value can be infinite if the limits of integration are infinite or if the function being integrated has an infinite range. In these cases, the integral value will also be infinite.

How does the interval of the Riemann integral value relate to the accuracy of the integral?

The interval of the Riemann integral value does not directly determine the accuracy of the integral. However, a smaller interval (i.e. a smaller range of values) can lead to a more accurate approximation of the integral value. This is because a smaller interval allows for more precise calculations and a better representation of the function being integrated.

Similar threads

MHB Improper integral of an even function
Replies
2
Views
2K
I Is my interpretation of this three dimensional improper integral correct?
Replies
4
Views
2K
Disjoint intervals for Riemann Integral
Replies
2
Views
2K
I Infinite Series - Divergence of 1/n question
Replies
5
Views
447
I Definitions of the Riemann integral
Replies
14
Views
2K
I Original definition of Riemann Integral and Darboux Sums
Replies
14
Views
3K
I Riemann integrability with a discontinuity
Replies
10
Views
3K
B Another proof of the existence of extreme values on open intervals
Replies
9
Views
1K
MHB Finding an Integral for a given Riemann Sum
Replies
8
Views
2K
I Riemann integrability and uniform convergence
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top