Intuitive Proof: $\omega \times \omega$ is Countable

[evinda]

Proposition:
The set $\omega \times \omega$ is equinumerous with $\omega$, i.e. the set $\omega \times \omega$ is countable.

"Intuitive Proof"

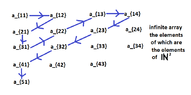
$$\mathbb{N}^2=\{ (n,m): n,m \in \mathbb{N} \}$$

View attachment 3825

$$1 \mapsto a_{11}$$
$$2 \mapsto a_{12}$$
$$3 \mapsto a_{31}$$
$$4 \mapsto a_{22}$$
$$5 \mapsto a_{13}$$
$$6 \mapsto a_{14}$$
$$7 \mapsto a_{23}$$
$$\ \ \ \ \cdots \cdots \\ \ \ \ \ \cdots \cdots \\ \ \ \ \ \cdots \cdots$$Could you explain me the intuitive proof? (Thinking)

 

[Evgeny.Makarov]

This process gives every pair of natural numbers a single natural number and vice versa: e.g., (1, 3) corresponds to 5. This correspondence is a bijection.

 

[evinda]

So do we know that it is an injection because we pair each natural number to a diferent pair of natural numbers?
Also do we know that it is a surjection because there are both infinitely many natural numbers and pairs of natural numbers, so for each pair there will be a single element that we can correspond to the pair? (Thinking)

 

[Evgeny.Makarov]

Yes, pretty much.

 

[evinda]

Then it is given the following proof:

We define recursively the function $T: \omega \to \omega$ as follows:

$T(0)=0 \ \ \ \ \ T(n+1)=T(n)+n=1$

which has the following properties:

• it is strictly increasing
• it is 1-1
• show that $(\forall y \in \omega) (\exists x \in \omega) (T(x) \leq y<T(x+1))$

We define the function $J(m,n)=T(m+n)+n (\langle m,n \rangle=m,n)$.

We will show that $J$ is 1-1 and surjective, i.e. $J: \omega \times \omega \overset{\text{surjective}}{\longrightarrow} \omega$.

• $J$ is 1-1.
  
  Let $\langle m,n \rangle \neq \langle k,l \rangle , m,n,k,l \in \omega$.
  
  First case: $m+n=n+k$
  
  If we had $J(m,n)=J(k,l)$ then $T(m+n)+n=T(k+l)+l \rightarrow n=l$ and since $m+n=k+l$ we have that $m=k$ that implies that $\langle m,n \rangle= \langle k, l \rangle$, contradiction.
  Thus $J(m,n) \neq J(k,l)$.Second case: $m+n \neq k+l$
  
  We suppose without loss of generality that $m+n<k+l$. Then $m+n+1 \leq k+l$ and so $T(m+n+1) \leq T(k+l)$.
  
  We have that $J(m,n)=T(m+n)+n<T(m+n)+n+1=T(m+n+1) \leq T(k+l)<T(k+l)+l=J(k,l)$
  
  Thus, $J(m,n) \neq J(k,l)$.
  
• Show that $J$ is surjective.
  

Is this proof related to the other proof? Do we have the same correspondance?