- #1
gfd43tg
Gold Member
- 950
- 50
Hello, I am working on this problem
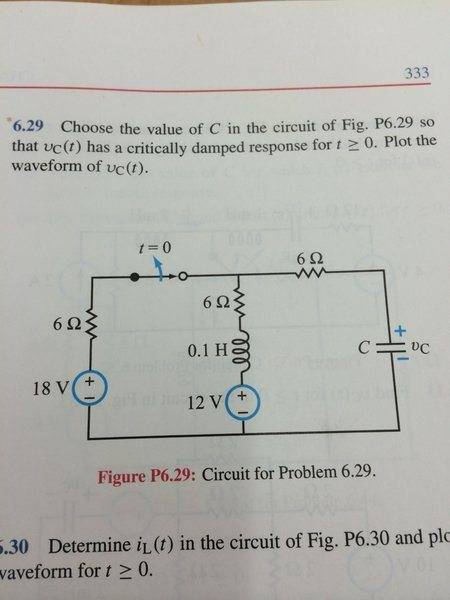
However, I am getting a 900t term that the solution is lacking. I am wondering if what I did was wrong. My formula is consistent with the formula for a series RLC circuit that is critically damped.
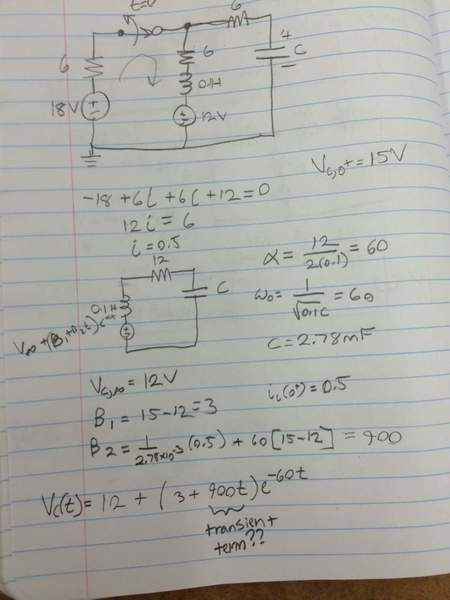
However, I am getting a 900t term that the solution is lacking. I am wondering if what I did was wrong. My formula is consistent with the formula for a series RLC circuit that is critically damped.