Is my work correct? (Two students running on a track)

[bekishe004]

Homework Statement

I am not sure if my working out is correct because I have 2 values

Relevant Equations

d=vt

Two students run around a 400m sport field. A goes anticlockwise (i.e., 1-2-3-4-1) while Bruns clockwise (i.e., 1-4-3-2-1). Students A and B can run 400 m in 75.0 s and 65.0 s,respectively.

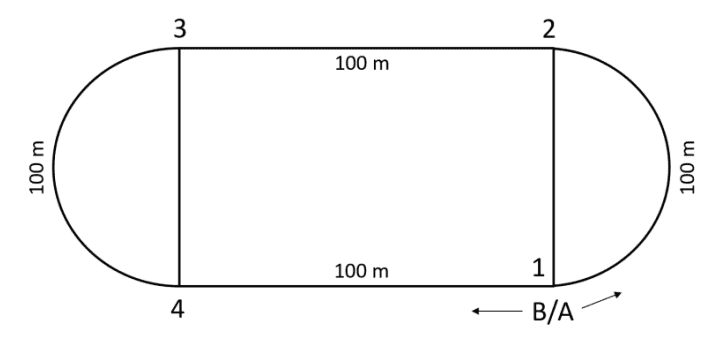
Students A and B should meet at some point of the run. Where do they meet? Assume the cross-over position is P. What is their relative velocity at position P.
My working out:

Lets first find the relative velocity, which going to be 12

t=d/v
400/12 = 33.33... seconds

d = 5.33 * 33.33 = 177.67m
d= 6.67 * 33.33 = 222.32m

Now, whats confusing me is that I have two values and I am not sure what to do with them.

Any help will be appreciated :)

 

[bekishe004]

I hope this time and I haven't violated any rules.

 

[kuruman]

I hope this time and I haven't violated any rules.

I don't think so. How do you know that the relative velocity is "12"? 12 what? What are 5.33 and 6.67 and how did you get them?

Suppose you cut the track at point 1 and you straighten it out to get a straight 400-m track. The runners start at each end going towards each other. Do you see where this is going?

 

[bekishe004]

I don't think so. How do you know that the relative velocity is "12"? 12 what? What are 5.33 and 6.67 and how did you get them?

Suppose you cut the track at point 1 and you straighten it out to get a straight 400-m track. The runners start at each end going towards each other. Do you see where this is going?

Sure,

Student A v=d/t= 400/75=5.33m/s
Student B v=d/t=400/65=6.15m/s

It appears I made a mistake, its not 6.67 but 6.15m/s my bad

"Suppose you cut the track at point 1 and you straighten it out to get a straight 400-m track. The runners start at each end going towards each other. Do you see where this is going?"
Not really sorry

 

[kuruman]

Not really sorry

In the oval track, the runners start and meet at point P such that the sum of their distances from their respective starting points is 400 m.

In the straight track, the runners start and meet at point P such that the sum of their distances from their respective starting points is 400 m.

If you can find P in the straight track case, you have found point P in the oval track case.

Now do you see?

 

[bekishe004]

Ohhh

In the oval track, the runners start and meet at point P such that the sum of their distances from their respective starting points is 400 m.

In the straight track, the runners start and meet at point P such that the sum of their distances from their respective starting points is 400 m.

If you can find P in the straight track case, you have found point P in the oval track case.

Now do you see?

 

[bekishe004]

In the oval track, the runners start and meet at point P such that the sum of their distances from their respective starting points is 400 m.

In the straight track, the runners start and meet at point P such that the sum of their distances from their respective starting points is 400 m.

If you can find P in the straight track case, you have found point P in the oval track case.

Now do you see?

With my new values and understanding,

this what I am getting

5.33t+6.15t=400
11.48x=400
x=400/11.48

400/11.48 = 34.84s

5.33*34.84 = 185.70
6.15*34.84 = 214.27

sum of two these values gives 400m

I still kinda confused where I go from here

 

[bekishe004]

With my new values and understanding,

this what I am getting

5.33t+6.15t=400
11.48x=400
x=400/11.48

400/11.48 = 34.84s

5.33*34.84 = 185.70
6.15*34.84 = 214.27

sum of two these values gives 400m

I still kinda confused where I go from here

I don't think I am wrong because when Student A travels to 214m thats where Student B who has travelled 185 m.

 

[bekishe004]

I want to thank everyone who has helped me or trying too.

I did pretty well in chemistry and precalc but I dunno why physics is kicking my butt

 

[kuruman]

With my new values and understanding,

this what I am getting

5.33t+6.15t=400
11.48x=400
x=400/11.48

400/11.48 = 34.84s

5.33*34.84 = 185.70
6.15*34.84 = 214.27

sum of two these values gives 400m

I still kinda confused where I go from here

Answer the question. Where is point P?

 

[Lnewqban]

I still kinda confused where I go from here

Student B is faster than student A.
Therefore, when B completes 400 m, he will be at point 1 again, but student A has not reached point 1 yet (he may be moving between points 4 and 1).

The meeting time must be the same for A and B and its value should be between 65 and 75 seconds.

You could create a distance versus time diagram for both students in order to visualize the relative movements more clearly.

 

[bekishe004]

Answer the question. Where is point P?

I am unsure

but am I close?

 

[bekishe004]

Student B is faster than student A.
Therefore, when B completes 400 m, he will be at point 1 again, but student A has not reached point 1 yet (he may be moving between points 4 and 1).

The meeting time must be the same for A and B and its value should be between 65 and 75 seconds.

You could create a distance versus time diagram for both students in order to visualize the relative movements more clearly.

I have tried that it didnt help me out

 

[Tom.G]

Can you answer where they meet if on a straight track?

 

[haruspex]

I have tried that it didnt help me out

View attachment 332720

Your graph is as though they go the same direction around. Try reversing one.

 

[bekishe004]

Your graph is as though they go the same direction around. Try reversing one.

Can you help me with that please?
I know that y=6.15x
and y=5.33x
I am so confused

 

[bekishe004]

Your graph is as though they go the same direction around. Try reversing one.

This might be it
I apologise for being slow
Again, thank you to everyone for helping me