Gamma Anon
- 11
- 4
- TL;DR Summary
- Length contraction paradox that I created but cannot solve, please help (Not homework)
Hi Physics Forums,
I've devised a thought experiment called the "Killer Crate Paradox" to put a spotlight on an issue I'm having, with regards to understanding length contraction, specifically in instances where multiple objects are observable and they have different velocities and directions of motion.
Please read it (see below) and provide your enlightened thoughts in the comments.
The Killer Crate Paradox
Two police officers, Bob and Alice, receive intel about an assassination plot against prominent exiled physicist, Dr Katze, that they protect from the vindictive regime she has fled. The assassins plan to attack the physicist while she is on a train she regularly catches, and want to make it look like an accident at first glance, to provide them time to escape.
While the train is heading due North along its route and Dr Katze sits by her usual Western facing window, the assassins intend to launch a cargo crate at a high velocity that will enter the carriage via the window and strike her. Because the train will be traveling at 0.5c, the assassins intend to launch the crate in the North East direction, at a speed of 0.70711c (or exactly (0.5c)^0.5 ), so that the Northbound velocity vector of the crate is the same as the Northbound velocity of the train.
In order to ensure that it kills Dr Katze, they have designed the crate to be as large as it possibly can and still pass through the window. The crate they have made is cube shaped, with dimensions (500mm x 500m x 500mm) minutely shorter than the square window frame (501mm x 501mm), when both are at rest, which should allow it to completely slide through the window frame and strike the physicist, despite its large size.
Bob ponders the feasibility of the plot, using the knowledge of special relativity he has picked up from Dr Katze, and decides that the plot has some potential of being successful, and thus it is far too dangerous for the physicist to continue catching this train.
As the crate is traveling at the same speed in the Northbound direction, Bob reasons, it would appear to anyone on the train that the crate is traveling in an eastwards direction relative to the carriages. While the crate would no longer look like a cube due to length contraction between the eastern and western faces of the crate, the distance between the northern and southern faces of the crate would appear the same as it is at rest, allowing the crate to snuggly slide through the window frame, assuming the assassins get the launch timing right.
Alice is more sceptical of the likelihood that such a plot would be successful, having taken the perspective of someone stationary relative to the ground. In that frame of reference, the distance between the North Eastern edge and the South Western edge of the crate will have contracted, as this is the direction of motion, while the distance between the North Western edge and the South Eastern edge will be the same as when the crate is at rest.
As the shape of the crate would be rhombohedron once launched, and the train's windows are narrowed as a result of length contraction in the direction of motion, Alice reasons that it will be impossible for the crate launch to be timed in such a way, that the crate will snuggly slide through the window.
Diagram of the crate and window* (Ground frame of reference)
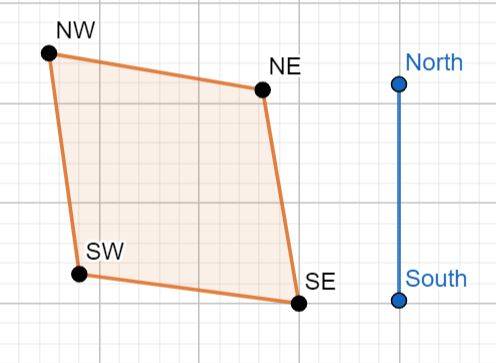
*Dimesions not exact and are for illustrative purposes only
Distance between SW and NE will be 500mm as a result of length contraction
Distance between SE and NW as it is at rest (~707.1mm) due to being perpedicular to the direction of motion
Distance between South and North ~433.9mm as a result of length contraction
If the Assassins manage to line up the South Eastern edge of the crate with the Southern edge of the window frame, by timing the launch correctly, the North Western corner will be further North than the Northern edge of the window frame. As a result, the crate will collide with the Northern edge of the window frame.
Bob and Alice see the merits of each other’s arguments and come to the realization that either their understanding of Special Relativity is wrong or they have just picked up a flaw. They reason that the outcome of the two perspectives must be the same; either the crate can slide snugly through the window if timing is right or it will collide with the window frame or carraige no matter the timing.
Thanks for reading
γ
I've devised a thought experiment called the "Killer Crate Paradox" to put a spotlight on an issue I'm having, with regards to understanding length contraction, specifically in instances where multiple objects are observable and they have different velocities and directions of motion.
Please read it (see below) and provide your enlightened thoughts in the comments.
The Killer Crate Paradox
Two police officers, Bob and Alice, receive intel about an assassination plot against prominent exiled physicist, Dr Katze, that they protect from the vindictive regime she has fled. The assassins plan to attack the physicist while she is on a train she regularly catches, and want to make it look like an accident at first glance, to provide them time to escape.
While the train is heading due North along its route and Dr Katze sits by her usual Western facing window, the assassins intend to launch a cargo crate at a high velocity that will enter the carriage via the window and strike her. Because the train will be traveling at 0.5c, the assassins intend to launch the crate in the North East direction, at a speed of 0.70711c (or exactly (0.5c)^0.5 ), so that the Northbound velocity vector of the crate is the same as the Northbound velocity of the train.
In order to ensure that it kills Dr Katze, they have designed the crate to be as large as it possibly can and still pass through the window. The crate they have made is cube shaped, with dimensions (500mm x 500m x 500mm) minutely shorter than the square window frame (501mm x 501mm), when both are at rest, which should allow it to completely slide through the window frame and strike the physicist, despite its large size.
Bob ponders the feasibility of the plot, using the knowledge of special relativity he has picked up from Dr Katze, and decides that the plot has some potential of being successful, and thus it is far too dangerous for the physicist to continue catching this train.
As the crate is traveling at the same speed in the Northbound direction, Bob reasons, it would appear to anyone on the train that the crate is traveling in an eastwards direction relative to the carriages. While the crate would no longer look like a cube due to length contraction between the eastern and western faces of the crate, the distance between the northern and southern faces of the crate would appear the same as it is at rest, allowing the crate to snuggly slide through the window frame, assuming the assassins get the launch timing right.
Alice is more sceptical of the likelihood that such a plot would be successful, having taken the perspective of someone stationary relative to the ground. In that frame of reference, the distance between the North Eastern edge and the South Western edge of the crate will have contracted, as this is the direction of motion, while the distance between the North Western edge and the South Eastern edge will be the same as when the crate is at rest.
As the shape of the crate would be rhombohedron once launched, and the train's windows are narrowed as a result of length contraction in the direction of motion, Alice reasons that it will be impossible for the crate launch to be timed in such a way, that the crate will snuggly slide through the window.
Diagram of the crate and window* (Ground frame of reference)
*Dimesions not exact and are for illustrative purposes only
Distance between SW and NE will be 500mm as a result of length contraction
Distance between SE and NW as it is at rest (~707.1mm) due to being perpedicular to the direction of motion
Distance between South and North ~433.9mm as a result of length contraction
If the Assassins manage to line up the South Eastern edge of the crate with the Southern edge of the window frame, by timing the launch correctly, the North Western corner will be further North than the Northern edge of the window frame. As a result, the crate will collide with the Northern edge of the window frame.
Bob and Alice see the merits of each other’s arguments and come to the realization that either their understanding of Special Relativity is wrong or they have just picked up a flaw. They reason that the outcome of the two perspectives must be the same; either the crate can slide snugly through the window if timing is right or it will collide with the window frame or carraige no matter the timing.
Thanks for reading
γ