END
- 36
- 4
I have the following system of equations with variables ##a,m##, and I'm wondering—can this system be solved symbolically/analytically?
\begin{align}
m &= 100 + \frac{ \left( 200 \frac{\ln{\frac{1}{2}}}{26.8} \right) }{\left(\dfrac{\ln{\frac{1}{2}}}{26.8} + a \right)}
\\ \\
50 &= me^{-a\left( 19.9 \right)}- \frac{ \left( 200 \frac{\ln{\frac{1}{2}}}{26.8} \right) \exp{ \left(\dfrac{\ln{\frac{1}{2}}}{26.8} \cdot 19.9 \right) }}{\left(\dfrac{\ln{\frac{1}{2}}}{26.8} + a \right)}
\end{align}
(What are some ways to recognize that a problem does or does not have an analytic solution?)
For this specific example, I understand the answers can be numerically approximated to
\begin{align}
a &\approx 0.092409
\\
m &\approx 22.2674
\end{align}
Via such numerical methods as a graph:
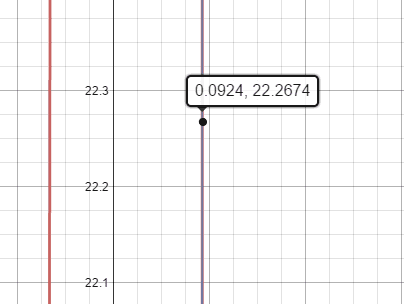
or other computational device such as WolframAlpha [(link to this problem). For this specific problem, WolframAlpha only provided a numerical approximation.
Note: The variables in the WolframAlpha link are ## a, n ## respectively
\begin{align}
m &= 100 + \frac{ \left( 200 \frac{\ln{\frac{1}{2}}}{26.8} \right) }{\left(\dfrac{\ln{\frac{1}{2}}}{26.8} + a \right)}
\\ \\
50 &= me^{-a\left( 19.9 \right)}- \frac{ \left( 200 \frac{\ln{\frac{1}{2}}}{26.8} \right) \exp{ \left(\dfrac{\ln{\frac{1}{2}}}{26.8} \cdot 19.9 \right) }}{\left(\dfrac{\ln{\frac{1}{2}}}{26.8} + a \right)}
\end{align}
(What are some ways to recognize that a problem does or does not have an analytic solution?)
For this specific example, I understand the answers can be numerically approximated to
\begin{align}
a &\approx 0.092409
\\
m &\approx 22.2674
\end{align}
Via such numerical methods as a graph:
or other computational device such as WolframAlpha [(link to this problem). For this specific problem, WolframAlpha only provided a numerical approximation.
Note: The variables in the WolframAlpha link are ## a, n ## respectively