KDPhysics
- 73
- 24
- TL;DR Summary
- If I randomly paint three objects without looking at them, are these objects in a superposition?
Suppose a blind man builds a machine that paints three apples with three colors, either red, blue or green. Once the machine has done this, are the three apples in the following superposition:
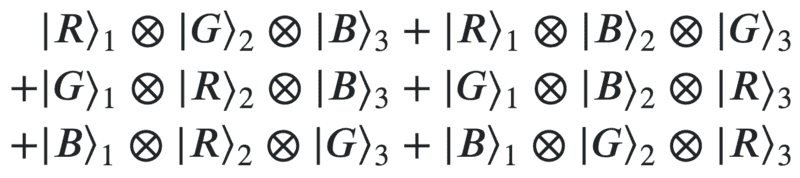
or is the wavefunction just one of
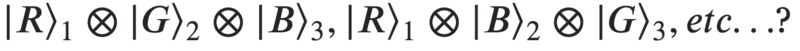
It feels like because the man is blind, the apples should be in a superposition as any measurement (say by asking someone else to check the colour of the apple) will lead to the wavefunction collapsing to one of the states in the superposition. However, on the other hand it feels like because the machine definitely assigns a colour to each apple, the wave-function should not be in a superposition. So which is it?
or is the wavefunction just one of
It feels like because the man is blind, the apples should be in a superposition as any measurement (say by asking someone else to check the colour of the apple) will lead to the wavefunction collapsing to one of the states in the superposition. However, on the other hand it feels like because the machine definitely assigns a colour to each apple, the wave-function should not be in a superposition. So which is it?