Dario56
- 289
- 48
Suppose there is a cylindrical (pellet) sample in the oxygen atmosphere as shown on the photo attached. Oxygen diffuses from the outside to the sample interior everywhere on the outer surface of the sample. From the photo, it can be seen that diffusion profile of oxygen is measured in the axial direction of the cylinder. In another words, diffusion is regarded as one-dimensional even though the sample is three-dimensional. I'm not sure how is it possible that one-dimensional solution of the diffusion equation can be applied here?
Oxygen can move in all three dimensions and will do so if partial derivative of concentration is non-zero in the other two Cartesian coordinates (cylindrical coordinates are more appropriate here, but that's not super important for the question).
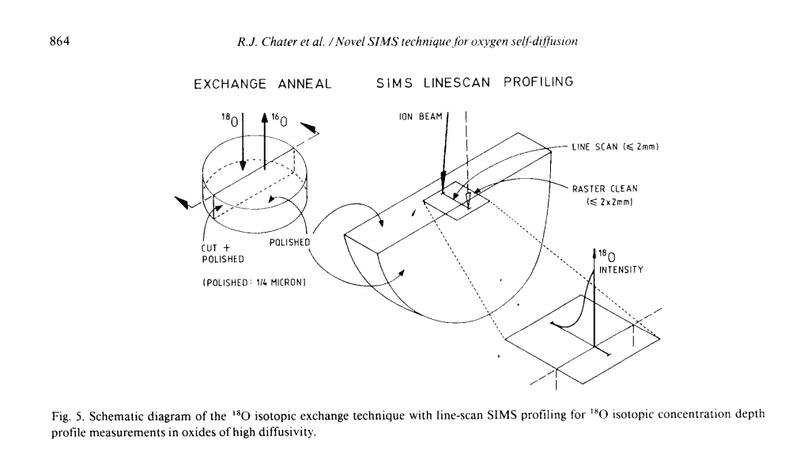
Oxygen can move in all three dimensions and will do so if partial derivative of concentration is non-zero in the other two Cartesian coordinates (cylindrical coordinates are more appropriate here, but that's not super important for the question).