MHB Janet's question at Yahoo Answers involving the Witch of Agnesi

[MarkFL]

Here is the question:

Parameterize and cartesian equation problem?

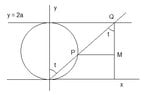
If P is any point on the circle C in the xy-plane of radius a >0 and center (0,a),let the straight line through the origin and P intersect the line y = 2a at Q, and let the line through P parallel to the x-axis intersect the line through Q parallel to the y-axis at M. As P moves around C, M traces out a curve called the witch of Agnesi.
For this curve, prove that it can be parameterized as W (t) = (2a tan t, 2a cos2 t). Fi- nally, use this parameterization to find a cartesian equation for the curve by eliminating the variable t.

Here is the original question:

Parameterize and cartesian equation problem? - Yahoo! Answers

I have posted a link there to this topic so the OP can find my response.

edit: I see now that the question has been deleted. According to the guidelines there it is okay to post links to a site to offer more information on a question, so I can only speculate as to why it was deleted. (Headbang)

 

[MarkFL]

Hello Janet,

Please refer to the following diagram:

View attachment 570

Let point M be at $(x_M,y_M)$, and point P be at $(x_P,y_P)$

As you can see, we may state:

$\displaystyle \tan(t)=\frac{x_M}{2a}\,\therefore\,x_M=2a\tan(t)$

We may also state:

$\displaystyle \tan(t)=\frac{x_P}{y_M}$

$\displaystyle y_M=x_P\cot(t)=a\sin(2t)\cot(t)=2a\cos^2(t)$

I made the observation that:

$\displaystyle x_P=a\sin(2t)$ from the requirements:

$\displaystyle x_P(0)=0,\,x_P\left(\frac{\pi}{4} \right)=a,\,x_P\left(\frac{\pi}{2} \right)=0$

And so we have the parametrization:

$\displaystyle M(t)=\langle 2a\tan(t),2a\cos^2(t) \rangle$

Now, to eliminate the parameter to obtain a Cartesian representation of the curve, we may write:

$\displaystyle t=\tan^{-1}\left(\frac{x}{2a} \right)$

Now substituting into the y-component, we find:

$\displaystyle y=2a\cos^2\left(\tan^{-1}\left(\frac{x}{2a} \right) \right)=\frac{8a^3}{x^2+4a^2}$