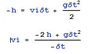Kinematics motion-an object falling and crossing a camera's view

[negation]

Homework Statement

You're a consultant on a movie set and the producer wants a car to drop so that it crosses the camera's field of view in time Δt.
The field of view has height h.
Derive an expression for the height above the top of the field of view from which the car should be released.

Homework Equations

None.

The Attempt at a Solution

 

[TSny]

In going from the first to the second equation in the attachment below, there are sign errors and an error of a factor of 2 somewhere.

Otherwise, I think your work is ok.

[EDIT: I just noticed you are missing a square in your last equation of your post. Also, in your next to last equation it looks like you switched the sign of the right hand side. I find it a bit hard to keep track of your signs because of your sign convention of taking g to be a negative number.]

 

[Chestermiller]

Let x = x_i=0 be the vertical location of the car at time t = 0
Let v = v_i=0 be the velocity of the car at time t = 0 (the car is dropped from rest)
Let x₁ be the vertical location of the car at time t = t₁ when the car reaches the top of the field of view
Let x₂=x₁-h be the vertgical location of the car at time t₂=t₁+ Δt when the car reaches the bottom of the field of view.

Write and equation for x₁ at time t₁.
Write and equation for x₁-h at time t₁+ Δt
Subtract the second equation from the first equation and solve for t₁ in terms of h, g, and Δt.

 

[negation]

In going from the first to the second equation in the attachment below, there are sign errors and an error of a factor of 2 somewhere.

Otherwise, I think your work is ok.

[EDIT: I just noticed you are missing a square in your last equation of your post. Also, in your next to last equation it looks like you switched the sign of the right hand side. I find it a bit hard to keep track of your signs because of your sign convention of taking g to be a negative number.]

reattempting

 

[negation]

In going from the first to the second equation in the attachment below, there are sign errors and an error of a factor of 2 somewhere.

Otherwise, I think your work is ok.

[EDIT: I just noticed you are missing a square in your last equation of your post. Also, in your next to last equation it looks like you switched the sign of the right hand side. I find it a bit hard to keep track of your signs because of your sign convention of taking g to be a negative number.]

This should be correct.

By the way, gravity works "downwards" so why shouldn't it be negative? Isn't it a logical corollary to ascribe a negative value to acceleration by gravity?

 

[TSny]

reattempting

You fixed the factor of 2, but you still have a sign error.

 

[negation]

You fixed the factor of 2, but you still have a sign error.

In the last equation? I forget to correct that. It should be -2h-2g(delta t)^2.
It's 2am in Australia and I'm really sleepy.
Would the equation be correct once it has been fixed?

 

[TSny]

By the way, gravity works "downwards" so why shouldn't it be negative? Isn't it a logical corollary to ascribe a negative value to acceleration by gravity?

The usual convention is to let g stand for the magnitude of the acceleration of gravity. Thus, g would be a positive number. In this convention you would have the following:

If you choose upward as positive for the y-axis, then the y-component of the acceleration of gravity would be written -g with a negative sign out front of the positive number g.

If you choose downward as positive for the y-axis, then the y-component of the acceleration of gravity would be written +g, or just g, where again g is a positive number.

(For this problem, it would probably be easier to keep track of signs if you choose the y-axis going downward as positive direction.)

 

[TSny]

In the last equation? I forget to correct that. It should be -2h-2g(delta t)^2.
It's 2am in Australia and I'm really sleepy.
Would the equation be correct once it has been fixed?

You still have a sign error in the equation below

 

[TSny]

If you could type in your equations rather than using attachments, it would be much easier to "cut and paste" specific equations from one post to another.

 

[Chestermiller]

View attachment 65001
This should be correct.

By the way, gravity works "downwards" so why shouldn't it be negative? Isn't it a logical corollary to ascribe a negative value to acceleration by gravity?

You lost the exponent of 2 on the right hand side of the equation.

 

[negation]

you lost the exponent of 2 on the right hand side of the equation.

 

[negation]

If you could type in your equations rather than using attachments, it would be much easier to "cut and paste" specific equations from one post to another.

Unfortunately, I haven't the time to learn latex. But I will soon.

I'm still quite unclear about the signs involving the acceleration due to gravity. Could you give a mathematical example?
I would have thought this would be correct. I give acceleration due to gravity a negative sign to denote an opposing direction relative to a positive velocity value for an object traveling upwards.

 

[Chestermiller]

Unfortunately, I haven't the time to learn latex. But I will soon.

I'm still quite unclear about the signs involving the acceleration due to gravity. Could you give a mathematical example?
I would have thought this would be correct. I give acceleration due to gravity a negative sign to denote an opposing direction relative to a positive velocity value for an object traveling upwards.
View attachment 65009

This looks correct, and the final answer you gave in the previous post looks correct also. If it were me, I would have multiplied the numerator and denominator within the parenthesis by minus 1, and I would also have taken the (Δt) in the denominator out of the parenthesis and combined it with the g in the denominator to obtain g(Δt)². But that's just me. I like to look at the math more "cleanly."

 

[TSny]

I'm still quite unclear about the signs involving the acceleration due to gravity. Could you give a mathematical example?
I would have thought this would be correct. I give acceleration due to gravity a negative sign to denote an opposing direction relative to a positive velocity value for an object traveling upwards.

If you take the y-axis upward as positive, then the y-component of the acceleration of gravity, a_y, will be a negative number. The usual way to express this is

a_y = -g where g itself is a positive number.

This is equivalent to writing a_y = g where g is now a negative number.

See

http://cnx.org/contents/031da8d3-b525-429c-80cf-6c8ed997733a@7.31:14

for the typical textbook discussion of the use of g for the magnitude of the acceleration of gravity. You'll see a few examples worked out. (It might take a few moments for the page to load completely.)

 

[TSny]

View attachment 65008

In the attachment below, note how you somehow added a negative sign on the right side of the equation in going from the first to the second equation.

Also, on the left side of the second equation, the denominator should not have a negative sign (assuming your convention that g is a negative number). This error won't matter here since you are squaring the entire quantity.

In your last equation, the denominator on the right side should not have a negative sign. This negative sign is the one you somehow added when going from the first to the second equation.

You can see how the overall signs don't agree for the left and right sides of the last equation. On the left side, you have y_f - y_i. So, the left hand side is overall negative because y_f is less than y_i. But the right hand side of your equation as written will give a positive quantity overall due to the error of the negative sign in the denominator.

Also, as you have already noted, the right hand side of the last equation still has a missing factor of 2 in the quantity inside the parentheses. (You have the factors of 2 correct in the next to last equation.)

 

[negation]

In the attachment below, note how you somehow added a negative sign on the right side of the equation in going from the first to the second equation.

Also, on the left side of the second equation, the denominator should not have a negative sign (assuming your convention that g is a negative number). This error won't matter here since you are squaring the entire quantity.

In your last equation, the denominator on the right side should not have a negative sign. This negative sign is the one you somehow added when going from the first to the second equation.

You can see how the overall signs don't agree for the left and right sides of the last equation. On the left side, you have y_f - y_i. So, the left hand side is overall negative because y_f is less than y_i. But the right hand side of your equation as written will give a positive quantity overall due to the error of the negative sign in the denominator.

Also, as you have already noted, the right hand side of the last equation still has a missing factor of 2 in the quantity inside the parentheses. (You have the factors of 2 correct in the next to last equation.)

Is this now valid?

 

[TSny]

Yes, that looks good.