gfd43tg
Gold Member
- 947
- 48
Hello, I was just watching a youtube video deriving the equation for the Hamiltonian for the harmonic oscillator, and I am also following Griffiths explanation. I just got stuck at a part here, and was wondering if I could get some help understanding the next step (both the video and book glanced over this part)
Video Link
The derivation starts at about 8:00
First defining
$$\hat {a}_{\pm} = \frac {1}{\sqrt{2 \hbar m \omega}}( \mp i \hat {p} + m \omega \hat {x})$$
$$ \hat {a}_{-} \hat {a}_{+} = \frac {1}{2 \hbar m \omega}(i \hat {p} + m \omega \hat {x})(-i \hat {p} + m \omega \hat {x}) $$
$$ = \frac {1}{2 \hbar m \omega}( \hat {p}^{2} + i m \omega \hat {p} \hat {x} - i m \omega \hat {x} \hat {p} + m^{2} \omega^{2} \hat {x}^{2}) $$
$$ = \frac {1}{2 \hbar m \omega}( \hat {p}^{2} - i m \omega (\hat {x} \hat {p} - \hat {p} \hat {x}) + m^{2} \omega^{2} \hat {x}^{2})$$
And I know the commutator ##[\hat {x}, \hat {p}] = i \hbar##
$$ = \frac {1}{2 \hbar m \omega}( \hat {p}^{2} - i m \omega ( i \hbar) + m^{2} \omega^{2} \hat {x}^{2} )$$
At this point both the video and Griffiths stop, although each do something different
I have no idea how Griffiths goes from this
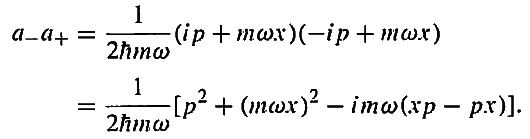
To this
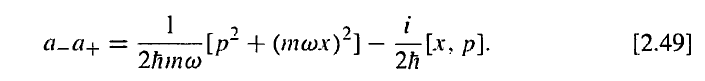
I will continue with what I was doing,
$$ = \frac {1}{2 \hbar m \omega}( \hat {p}^{2} + m \omega \hbar + m^{2} \omega^{2} \hat {x}^{2})$$
$$ = \frac {1}{2 \hbar m \omega}\hat {p}^{2} + \frac {1}{2 \hbar^{2} m^{2} \omega^{2}} + \frac {m \omega \hat {x}^{2}}{2 \hbar} $$
And from here I am not sure how both the video and Griffiths conclude

How do I get to the answer from my steps? Since I am not skipping..
Video Link
The derivation starts at about 8:00
First defining
$$\hat {a}_{\pm} = \frac {1}{\sqrt{2 \hbar m \omega}}( \mp i \hat {p} + m \omega \hat {x})$$
$$ \hat {a}_{-} \hat {a}_{+} = \frac {1}{2 \hbar m \omega}(i \hat {p} + m \omega \hat {x})(-i \hat {p} + m \omega \hat {x}) $$
$$ = \frac {1}{2 \hbar m \omega}( \hat {p}^{2} + i m \omega \hat {p} \hat {x} - i m \omega \hat {x} \hat {p} + m^{2} \omega^{2} \hat {x}^{2}) $$
$$ = \frac {1}{2 \hbar m \omega}( \hat {p}^{2} - i m \omega (\hat {x} \hat {p} - \hat {p} \hat {x}) + m^{2} \omega^{2} \hat {x}^{2})$$
And I know the commutator ##[\hat {x}, \hat {p}] = i \hbar##
$$ = \frac {1}{2 \hbar m \omega}( \hat {p}^{2} - i m \omega ( i \hbar) + m^{2} \omega^{2} \hat {x}^{2} )$$
At this point both the video and Griffiths stop, although each do something different
I have no idea how Griffiths goes from this
To this
I will continue with what I was doing,
$$ = \frac {1}{2 \hbar m \omega}( \hat {p}^{2} + m \omega \hbar + m^{2} \omega^{2} \hat {x}^{2})$$
$$ = \frac {1}{2 \hbar m \omega}\hat {p}^{2} + \frac {1}{2 \hbar^{2} m^{2} \omega^{2}} + \frac {m \omega \hat {x}^{2}}{2 \hbar} $$
And from here I am not sure how both the video and Griffiths conclude
How do I get to the answer from my steps? Since I am not skipping..
Attachments
Last edited: