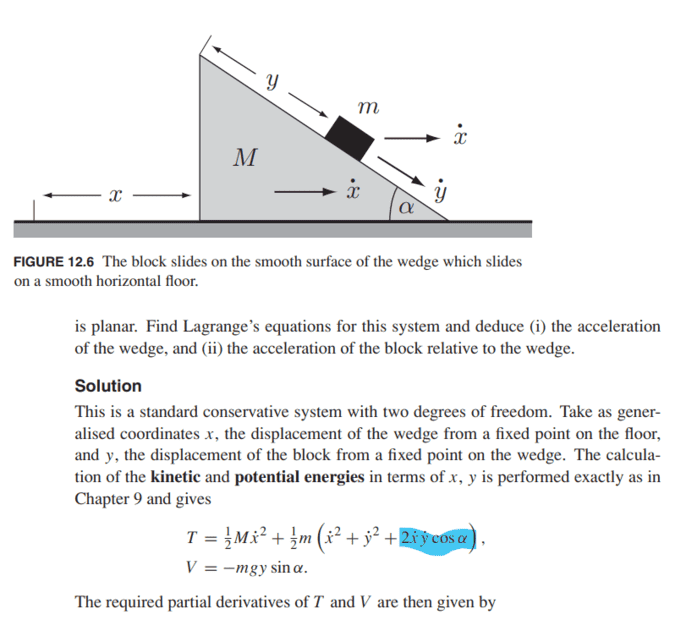
The discussion revolves around deriving the kinetic energy of a block on an inclined wedge and clarifying the origin of a specific term in the equation. Participants emphasize that the x and y components of the block's motion are not orthogonal, which complicates the calculation of its velocity. The highlighted term in question is identified as a cross term resulting from the correct expression for the block's horizontal velocity relative to the ground. The use of the cosine rule for vector addition of velocities is suggested as a valid approach to resolve the problem. The conversation highlights the importance of accurately representing the velocities of both the wedge and the block in the inertial frame.