LuccaP4
- 24
- 9
- Homework Statement
- Under the action of gravity, a particle of mass m slides on a conical surface without friction.
The conical surface has the form: ρ=z tanα
a. Find the motion equations using as coordinates θ and r (see picture).
b. Find r_max and r_min if α=30° and initial conditions are:
r(0)=a ; r ̇(0)=0 ; θ ̇^2 (0)=4√3 g/a
c. Find the effective potential and show that circular orbits are possible. Find the particle’s speed in circular orbits.
d. Assuming the particle in circular motion, find the oscillator constant and the period of oscillation for small perturbations of this motion.
- Relevant Equations
- Lagrange equations
I copy again the statement here:

So, I think I solved parts a to c but I don't get part d. I couldn't even start it because I don't understand how to set the problem.
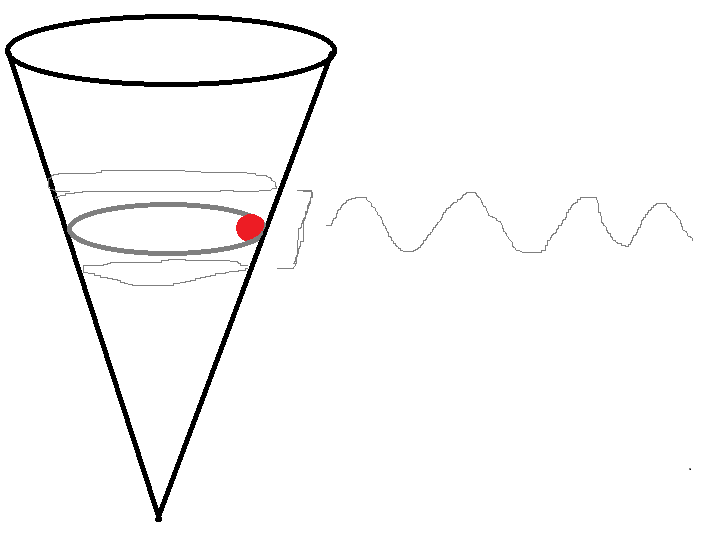
I think it refers to some kind of motion like this one in the picture, so I'll have a maximum and a minimum r, and I can get the energy and initial speed of a circular motion from part c, but I don't know how to use them.
I attach my resolution on the other parts.


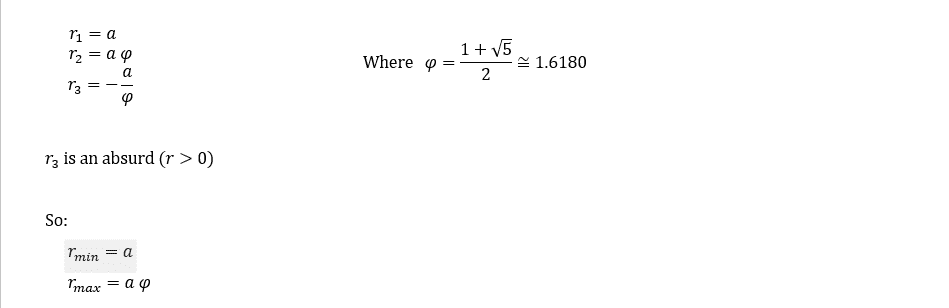


So, I think I solved parts a to c but I don't get part d. I couldn't even start it because I don't understand how to set the problem.
I think it refers to some kind of motion like this one in the picture, so I'll have a maximum and a minimum r, and I can get the energy and initial speed of a circular motion from part c, but I don't know how to use them.
I attach my resolution on the other parts.