OmCheeto
Gold Member
- 2,481
- 3,377
- TL;DR Summary
- Oddly linear statistics in health outcomes data collection
I've been entertaining myself since my retirement with science and maths problems.
My latest endeavor's plot seems a bit too linear, and I was curious if others have had such experiences with ongoing national level data collection?:
The U.S. CDC posts death data for Flu, Pneumonia, and Covid-19 on a weekly basis.
Each week, the posted data for all weeks changes.
Most annoying is the fact that I didn't start collecting the data delay until about 4 weeks ago.
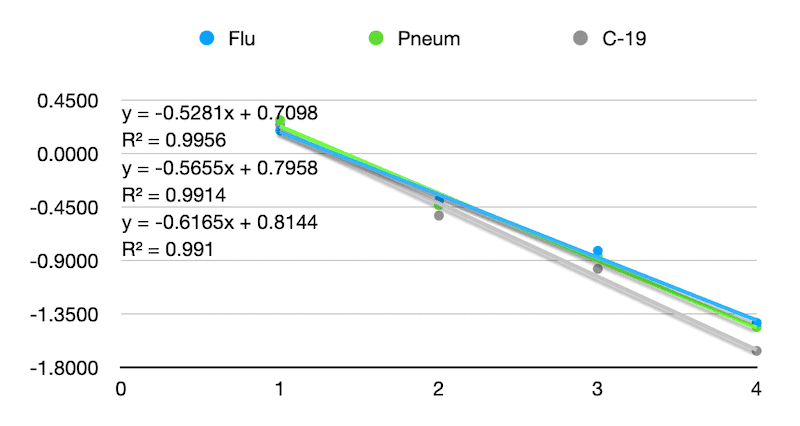
Most interestingly is that, as I mentioned previously, the data delay collection, graphed logarithmically, is exquisitely linear.
Raw data:
My latest endeavor's plot seems a bit too linear, and I was curious if others have had such experiences with ongoing national level data collection?:
The U.S. CDC posts death data for Flu, Pneumonia, and Covid-19 on a weekly basis.
Each week, the posted data for all weeks changes.
Most annoying is the fact that I didn't start collecting the data delay until about 4 weeks ago.
Most interestingly is that, as I mentioned previously, the data delay collection, graphed logarithmically, is exquisitely linear.
Raw data:
| Lag Week | Graphical Week | Week | week ending | Flu | Pneum | C-19 | ∑ | Flu | Pneum | C-19 | ∑ | Flu | Pneum | C-19 | ∑ | Flu | Pneum | C-19 | ∑ | Flu | Pneum | C-19 | ∑ | mult | mult | mult | mult | ||||||
| latest | data | collected | last | weeks | data | 2 | weeks | ago | 3 | weeks | ago | 4 | weeks | ago | 4 | 3 | 2 | 1 | lag | ||||||||||||||
| 0 | 63 | 11 | 3/16/2024 | 303 | 3,459 | 982 | 4744 | 292 | 3,343 | 961 | 4596 | 263 | 3041 | 887 | 4191 | 216 | 2527 | 755 | 3498 | 118 | 1186 | 356 | 1660 | 2.8578 | 1.3562 | 1.1319 | 1.0322 | ∑ | |||||
| 1 | 62 | 10 | 3/9/2024 | 384 | 3,644 | 1,047 | 5075 | 379 | 3,592 | 1,030 | 5001 | 368 | 3487 | 1002 | 4857 | 342 | 3193 | 933 | 4468 | 285 | 2497 | 748 | 3530 | 2.5678 | 1.4028 | 1.1521 | 1.0377 | Flu | |||||
| 2 | 61 | 9 | 3/2/2024 | 382 | 3,868 | 1,221 | 5471 | 381 | 3,848 | 1,215 | 5444 | 374 | 3797 | 1198 | 5369 | 365 | 3698 | 1164 | 5227 | 320 | 3292 | 1036 | 4648 | 2.9165 | 1.3688 | 1.1375 | 1.0347 | Pneum | |||||
| 3 | 60 | 8 | 2/24/2024 | 399 | 3,817 | 1,271 | 5487 | 397 | 3,789 | 1,269 | 5455 | 394 | 3744 | 1255 | 5393 | 388 | 3686 | 1234 | 5308 | 366 | 3512 | 1190 | 5068 | 2.7584 | 1.3007 | 1.1071 | 1.0219 | C-19 |