Learning DFT: Inhomogeneous Electron Gas (Hohenberg) Question

[yosty222]

TL;DR Summary

Where does the kinetic energy term of the hamiltonian come from? Is it an expectation value of the kinetic energy?

I'm reading through Hohenberg's seminal paper titled: "Inhomogeneous Electron Gas" that help lay the foundation for what we know of as Density Functional Theory (DFT) by proving the existence of a universal functional that exactly matches the ground-state energy of a system with a given interaction potential v(r). I'm working through this paper and I'm a bit confused on the exact form of the Hamiltonian he builds:

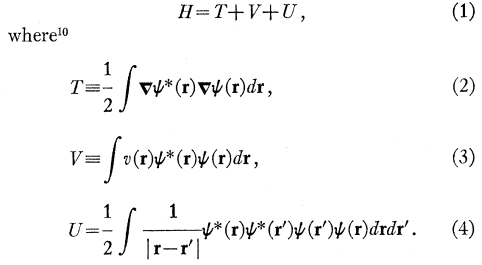
The form of kinetic energy looks like an expectation value, but not quite as I'd expect the expectation value of kinetic energy to look like $\int \psi^* \nabla^2 \psi$. The factor of $\frac{1}{2}$ out front makes me think it's coming from a $\frac{\mathbf{p^2}}{2m}$ term (with m = 1 in these units), but why does a $\nabla$ operator get attached to each $\psi^*$ and $\psi$?

Similarly, for the form of V (equation (3) above), is this expressing the contribution of the external potential $v(\mathbf{r})$ as an expectation value of the external potential over some volume d$\mathbf{r}$ then integrating over all space?

 

[TeethWhitener]

$\psi^*\nabla^2\psi=\nabla\cdot(\psi^*\nabla\psi)-\nabla\psi^*\cdot\nabla\psi$
The integral of $\nabla\cdot(\psi^*\nabla\psi)$ over all space will be zero, since it's equivalent to integrating over a surface at infinity, and the wavefunction and its derivative go to zero as $r\to\infty$.