Length of a third side of triangle

[Joystar77]

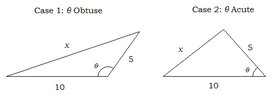
Math Problem: Find the length of the third side of a triangle if the area of the triangle is 18 and two of its sides have lengths of 5 and 10.

Which one of these are correct when I am working them out? If none of these are correct, then can somebody please help me solve this math problem step-by-step?

First way I worked out the problem:

A=18=0.5*5*10*sin(x)

x = 46 degrees

====

c^2 = 10^2+5^2-2*50*cos(46) = 55,53

third side:

c = 7,45

Second way I worked out the problem:

I know A = 18 units², a = 5 units, and b = 10 units

given A = (absin(C))/2

=> 18 = 25sin(C)

=> 18/25 = sin(C)

=> C = sin⁻¹(18/25)

given c² = a² + b² -2abcos(C)=> c² = 25 + 100 -100cos(sin⁻¹(18/25))

=> c = √(125 -100cos(sin⁻¹(18/25)))

=> c = √(125 - 4√301) units

=> c ≈ 7.4567 ( 4 dp)

Third way I worked out the problem:

Use Heron's formula for triangle:

Suppose the third side is x, and the others are 5 and 10, so by Heron formula, we get:

Area = sqrt(s(s-a)(s-b)(s-c))

where s=semi perimeter, a,b,c are sides of triangle, a=x, b=5, c=10

so, s=1/2.(x+5+10)

=1/2(x+15)

s-a= 1/2x +15/2 -x= 15/2-x/2

s-b=x/2+15/2-10/2=x/2+5/2

s-c=x/2+15/2-20/2=x/2-5/2

Area= sqrt(x/2+15/2)(15/2-x/2)(x/2+5/2)(x/2-5/…

324=(15/2+x/2)(15/2-x/2)(x/2+5/2)(x/2-…

324=(225/4 -x^2/4)(x^2/4-25/4)..multiply by 4 to get

1296=(225-x^2)(x^2-25)

225x^2-225*25-x^4+25x^2-1296=0

-x^4+250x^2-6921=0

-(x^4-250x^2+6921)=0

-((x^2-125)-8704)=0

(x^2-16sqrt34-125)(x^2+16sqrt34-125)=0

x^2=16sqrt34+125

x=sqrt(16sqrt 34+125)

=14.775

or

x^2=125-16sqrt34

x=sqrt(125-16sqrt34)

=5.63

So, the length of the third side is 14.775 or 5.63

I am really lost and confused on this problem.

 

[MarkFL]

I would look at the two case:

View attachment 1340

In both cases, we have:

$$A=\frac{1}{2}bh$$

$$18=25\sin(\theta)$$

Case 1:

$$\theta=\pi-\sin^{-1}\left(\frac{18}{25} \right)$$

Using the law of cosines, we may write:

$$x=\sqrt{10^2+5^2-2\cdot5\cdot10\cos\left(\pi-\sin^{-1}\left(\frac{18}{25} \right) \right)}$$

Case 2:

$$\theta=\sin^{-1}\left(\frac{18}{25} \right)$$

Using the law of cosines, we may write:

$$x=\sqrt{10^2+5^2-2\cdot5\cdot10\cos\left(\sin^{-1}\left(\frac{18}{25} \right) \right)}$$

You should be able to obtain an exact value for $x$ in both cases (you have already found the exact value for the acute case), and these do agree with the two positive roots that Heron's formula gives.

What do you find?

 

[johng1]

Hi,
It may be easier to assign coordinates in the problem. See the attachment:

View attachment 1342