Lewis H Ryder: Cartesian to Polar Coord Transformations

[Ayoub Tamin]

TL;DR

I had a problem understanding an example in the page 60-61 In Lewis's Ryder's Book

The example is about the transformation between the cartesian coordinates and polar coordinates using the definition

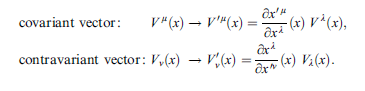
In lewis Ryder's solution, I got confused in this specific line

I really can't see how is that straightforward to find?

 

[strangerep]

I'm reasonably sure you're overthinking this (although there is a sign typo in his definition of $r$: his "$-1/2$" exponent should be "$1/2$").

Your boxed section is just the definition of partial derivative. I.e., $\frac{\partial x}{\partial r}$ means the derivative of $x$ by $r$, with $\theta$ treated as a constant. So... $$\frac{\partial x}{\partial r} ~=~ \frac{\partial (r \cos\theta)}{\partial r} ~=~ \cos\theta \, \frac{dr}{dr} ~=~ \cos\theta ~,$$and $$\frac{\partial r}{\partial x} ~=~ \frac{\partial (x^2+y^2)^{1/2}}{\partial x} ~=~ \frac{1}{2} (x^2+y^2)^{-1/2} (2x) ~=~ x/r ~=~ \dots$$(Can you complete the last step?)

 

[Ayoub Tamin]

I'm reasonably sure you're overthinking this (although there is a sign typo in his definition of $r$: his "$-1/2$" exponent should be "$1/2$").

Your boxed section is just the definition of partial derivative. I.e., $\frac{\partial x}{\partial r}$ means the derivative of $x$ by $r$, with $\theta$ treated as a constant. So... $$\frac{\partial x}{\partial r} ~=~ \frac{\partial (r \cos\theta)}{\partial r} ~=~ \cos\theta \, \frac{dr}{dr} ~=~ \cos\theta ~,$$and $$\frac{\partial r}{\partial x} ~=~ \frac{\partial (x^2+y^2)^{1/2}}{\partial x} ~=~ \frac{1}{2} (x^2+y^2)^{-1/2} (2x) ~=~ x/r ~=~ \dots$$(Can you complete the last step?)

Oh you are absolutely righ, I overthinked that haha and yes i can complete the last step ^^ thanks for your help I appreciate it