AlienGrey
- 19
- 10
- TL;DR Summary
- Thought experiment showing discrepancy in the speed of light for forward and backward light beams in a moving frame as viewed from a stationary frame
In the illustration below, a laser beam is emitted, and the time recorded, from the rear of a frame which is 150,000 km long and is moving at velocity 0.5 c to the right. When the beam reaches a half silvered mirror at the front of the frame, the frame being shown as a rectangle and using different colors for three different positions along its path of travel, half of the beam goes through the mirror to a sensor which records its time of arrival and the other half bounces from the mirror to the rear of the frame from whence it was emitted, striking a second sensor which also records the time. The frame was already up to speed when it emitted the beam at position one, shown in blue, so no acceleration effects are involved.
The time taken for the beam to reach the mirror, at position two shown in red, is 1 second in our stationary frame, having traveled 300,000 km, and the time taken for the reflected beam to reach the rear sensor is 0.33 second, the beam having traveled 100,000 km rearward (left) while the frame having moved ahead (right) 50,000 km by the time the beam hit the sensor, totaling the full length of the frame, 150,000 km, the frame's position shown in green. The one-way speed of light would be difficult to gauge in the real world, but this a thought experiment so it's a lot easier to do.
How do observers within the moving frame record the time taken for both the forward and rearward beams to be 0.5 second, as would be the case if the frame had been standing still? Or would they record the same times as we did in the stationary frame? For the time to be 0.5 second in both directions, their time would have to pass at 50% the rate of ours while the beam traveled forward, and it would have to pass at 150% the rate of ours on its rearward trip. How do you reach that outcome using a single time dilation and/or length contraction factor, considering how different they are? If you can explain how light speed can be recorded as 300,000 km/s in both directions in both frames, I think you deserve a Nobel Prize, because I suspect that Einstein wouldn't be able to do it using his equations.
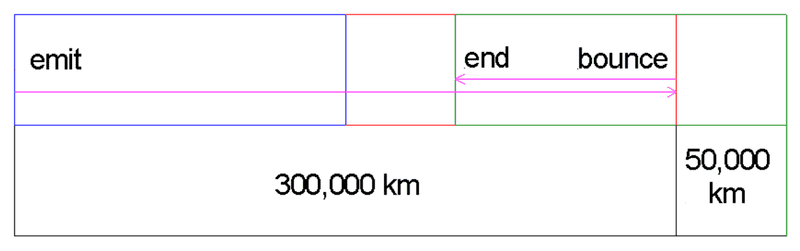
The time taken for the beam to reach the mirror, at position two shown in red, is 1 second in our stationary frame, having traveled 300,000 km, and the time taken for the reflected beam to reach the rear sensor is 0.33 second, the beam having traveled 100,000 km rearward (left) while the frame having moved ahead (right) 50,000 km by the time the beam hit the sensor, totaling the full length of the frame, 150,000 km, the frame's position shown in green. The one-way speed of light would be difficult to gauge in the real world, but this a thought experiment so it's a lot easier to do.
How do observers within the moving frame record the time taken for both the forward and rearward beams to be 0.5 second, as would be the case if the frame had been standing still? Or would they record the same times as we did in the stationary frame? For the time to be 0.5 second in both directions, their time would have to pass at 50% the rate of ours while the beam traveled forward, and it would have to pass at 150% the rate of ours on its rearward trip. How do you reach that outcome using a single time dilation and/or length contraction factor, considering how different they are? If you can explain how light speed can be recorded as 300,000 km/s in both directions in both frames, I think you deserve a Nobel Prize, because I suspect that Einstein wouldn't be able to do it using his equations.
Last edited: