ZPlayer
- 35
- 0
Hi, Everyone,
Problem asks to prove that limit of x^2 * sin^2 (y) / (x^2 + 2* y^2) as (x,y) approach (0,0) is 0 using delta-epsilon method. I think I solved it below. Let me know if I am write or wrong.
Thanks.
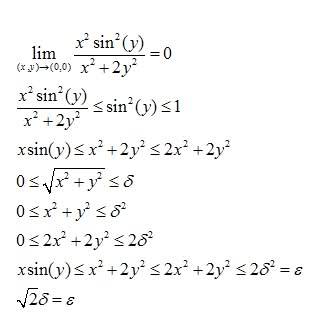
Problem asks to prove that limit of x^2 * sin^2 (y) / (x^2 + 2* y^2) as (x,y) approach (0,0) is 0 using delta-epsilon method. I think I solved it below. Let me know if I am write or wrong.
Thanks.