curious_ocean
- 36
- 7
- Homework Statement
- What is the limit as x--> -5?
- Relevant Equations
- What is the limit on the edge of a function's domain?
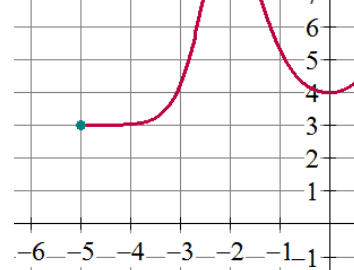
What is the limit of the function as x goes to -5 (e.g. in the graph below) if the domain of the function is only defined on the closed interval [-5,5]?
I realize that the right hand limit DOES exist and is equal to 3, but the left hand limit does not exist?
So does that mean that the overall limit does not exist?
Or since the domain does not exist to the left, is the left hand limit not needed for the overall limit?
Thanks for your help!
I realize that the right hand limit DOES exist and is equal to 3, but the left hand limit does not exist?
So does that mean that the overall limit does not exist?
Or since the domain does not exist to the left, is the left hand limit not needed for the overall limit?
Thanks for your help!
