Lynch101
Gold Member
- 772
- 85
- TL;DR Summary
- A few questions on Bell's inequality, which might serve as a means for helping me better understand Bell's Theorem, Hidden Variables & QM.
I was revisiting @DrChinese 's Bell's Theorem with Easy Math which sparked a few questions, which I am hoping might offer a potential path to a deeper understanding of Bell's Theorem and Quantum Mechanics (QM) in general.
The explanation uses light polarisation experiments to explain how we arrive at Bell's inequality.
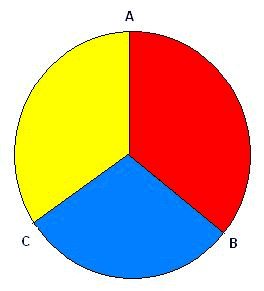

When it says above to "assume that a photon has 3 simultaneously real Hidden Variables (HV) A, B and C [at the angles]" does this only apply to Hidden variables theories with these specific characteristics? Is it possible to have a HV theory which doesn't have these 3 simultaneously real Hidden Variables.
There is probably some basic answer to this, but in trying to think more about Bell's theorem, I was wondering if it would be possible that the photons are simply polarised North and South, where the line of polarisation (the axis?) would be the hidden variable and can take any orientation within 360 degrees? I was thinking that this would mean that any photon would have a probability 0.5 of passing a polarisation filter. For any pair of particles, there would be a probability of ≥0.25 of both photons passing through their respective filters.

F = fails to pass filter
P = passes filter
P/F = photon 1 passes/photon 2 fails
Pass = both pass their respective filters.There is probably lots wrong in that, but that is where my thinking has taken me, so any help to point out where I've gone wrong or gaps in my understanding would be greatly appreciated.
The explanation uses light polarisation experiments to explain how we arrive at Bell's inequality.
We can't explain why a photon's polarization takes on the values it does at angle settings A, B and C. But we can measure it after the fact with a polarizer at one setting, and in some cases we can predict it for one setting in advance. The colors match up with the columns in Table 1 below. (By convention, the 0 degrees alignment corresponds to straight up.)
(Emphasis mine)ASSUME that a photon has 3 simultaneously real Hidden Variables A, B and C at the angles 0 degrees, 120 degrees and 240 degrees per the diagram above. These 3 Hidden Variables, if they exist, would correspond to simultaneous elements of reality associated with the photon's measurable polarization attributes at measurement settings A, B and C.
...
[W]e are simply saying that the answers to the 3 questions "What is the polarization of a photon at: 0, 120 and 240 degrees?" exist independently of actually seeing them. If a photon has definite simultaneous values for these 3 polarization settings, then they must correspond to the 8 cases ([1]...[8]) presented in Table 1 below. So our first assumption is that reality is independent of observation, and we will check and see if that assumption holds up.
There are only three angle pairs to consider in the above: A and B (we'll call this [AB]); B and C (we'll call this [BC]); and lastly A and C (we'll call this [AC]). If A and B yielded the same values (either both + or both -), then [AB]=matched and we will call this a "1". If A and B yielded different values (one a + and the other a -), then [AB]=unmatched and we will call this a "0". Ditto for [BC] and [AC]. If you consider all of the permutations of what A, B and C can be, you come up with the following table:
It is pretty obvious from the table above that no matter which of the 8 scenarios which actually occur (and we have no control over this), the average likelihood of seeing a match for any pair must be at least .333
...
We don't know whether [Cases [1] and [8]] happen very often, but you can see that for any case the likelihood of a match is either 1/3 or 3/3). Thus you never get a rate less than 1/3 as long as you sample [AB], [BC] and [AC] evenly.
...
The fact that the matches should occur greater than or equal to 1/3 of the time is called Bell's Inequality.
...
Bell also noticed that QM predicts that the actual value will be .250, which is LESS than the "Hidden Variables" predicted value of at least .333
...
If [the experimental tests] are NOT in accordance with the .333 prediction, then our initial assumption above - that A, B and C exist simultaneously - must be WRONG.
...
Experiments support the predictions of QM.
When it says above to "assume that a photon has 3 simultaneously real Hidden Variables (HV) A, B and C [at the angles]" does this only apply to Hidden variables theories with these specific characteristics? Is it possible to have a HV theory which doesn't have these 3 simultaneously real Hidden Variables.
There is probably some basic answer to this, but in trying to think more about Bell's theorem, I was wondering if it would be possible that the photons are simply polarised North and South, where the line of polarisation (the axis?) would be the hidden variable and can take any orientation within 360 degrees? I was thinking that this would mean that any photon would have a probability 0.5 of passing a polarisation filter. For any pair of particles, there would be a probability of ≥0.25 of both photons passing through their respective filters.
F = fails to pass filter
P = passes filter
P/F = photon 1 passes/photon 2 fails
Pass = both pass their respective filters.There is probably lots wrong in that, but that is where my thinking has taken me, so any help to point out where I've gone wrong or gaps in my understanding would be greatly appreciated.
Last edited: