Ask Why!
- 4
- 0
Magnet Phenomenon: The "divergent" region of a ring magnet
Here's a puzzler:
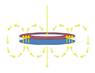
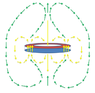
I have a NdFeB ring magnet, 1.75" outer diameter x 1.375" inner diameter x 0.25" thick, N40 grade. It is axially magnetized so that the north pole is toward one face and the south pole is toward the opposite face. The following image shows the well-known theoretical orientation of the magnetic field around the magnet, given that the north pole is on top:
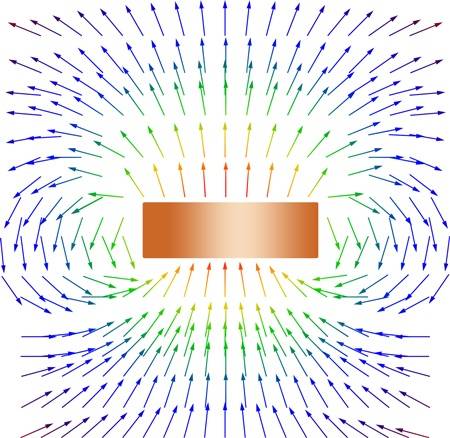
SIDE VIEW
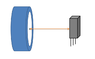
I have been in the lab determining the magnetic field orientation and approximate strength of the magnet using a linear Hall Effect sensor. The attached image shows the test configuration, with the orange arrow representing the dimension that was varied in the observance of the phenomenon. The image is not to scale.
If I move the sensor across the magnet, I get the expected readings: Saturation in one field orientation directly over the rim of the ring magnet, then a reversal of orientation in the open center of the magnet. BUT, if I take a reading over the center of the magnet from more than 0.5" away from the direct center along the cylindrical axis, the orientation of the magnetic field is the opposite of that observed over the center of the ring from within 0.5". I am having trouble explaining why this is the case.
The following leads me to strongly believe that this phenomenon is NOT DUE TO HYSTERESIS: The same effect is observable even if I allow the sensor to return to its quiescent voltage and then approach over the open center from a distance. The field is the reverse of the theoretical field indicated in the above image, until 0.5" from the center of the ring, at which point it reverses to the expected orientation.
The analogous effect is observable on the opposite side of the ring, that is, if we put south on top and kept the sensor in the same orientation.
Can anyone explain what is happening in what I have been calling the "divergent" region?
Please indicate if you are hypothesizing or applying accepted theory.
Here's a puzzler:
I have a NdFeB ring magnet, 1.75" outer diameter x 1.375" inner diameter x 0.25" thick, N40 grade. It is axially magnetized so that the north pole is toward one face and the south pole is toward the opposite face. The following image shows the well-known theoretical orientation of the magnetic field around the magnet, given that the north pole is on top:
SIDE VIEW
I have been in the lab determining the magnetic field orientation and approximate strength of the magnet using a linear Hall Effect sensor. The attached image shows the test configuration, with the orange arrow representing the dimension that was varied in the observance of the phenomenon. The image is not to scale.
If I move the sensor across the magnet, I get the expected readings: Saturation in one field orientation directly over the rim of the ring magnet, then a reversal of orientation in the open center of the magnet. BUT, if I take a reading over the center of the magnet from more than 0.5" away from the direct center along the cylindrical axis, the orientation of the magnetic field is the opposite of that observed over the center of the ring from within 0.5". I am having trouble explaining why this is the case.
The following leads me to strongly believe that this phenomenon is NOT DUE TO HYSTERESIS: The same effect is observable even if I allow the sensor to return to its quiescent voltage and then approach over the open center from a distance. The field is the reverse of the theoretical field indicated in the above image, until 0.5" from the center of the ring, at which point it reverses to the expected orientation.
The analogous effect is observable on the opposite side of the ring, that is, if we put south on top and kept the sensor in the same orientation.
Can anyone explain what is happening in what I have been calling the "divergent" region?
Please indicate if you are hypothesizing or applying accepted theory.