Magnitude of electric field E on a concentric spherical shell

[vcsharp2003]

Homework Statement

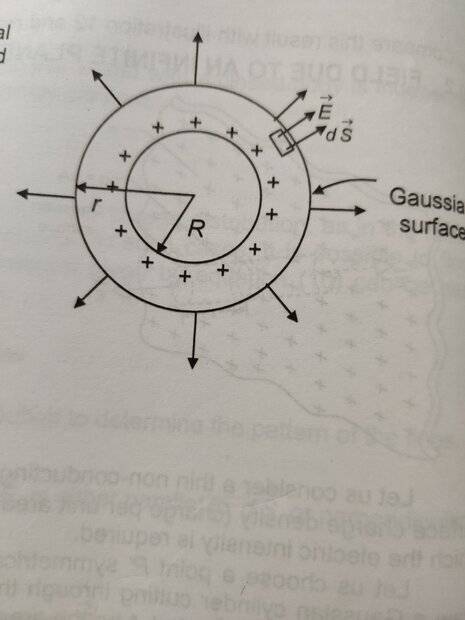
Why is magnitude of electric field the same at all points on an imaginary concentric spherical shell that is concentric to a real charged spherical shell? The charged spherical shell is inside the concentric spherical shell.

Relevant Equations

$E =\dfrac { Kq_1q_2} {r^2}$, which is the Coulomb's law in Electrostatics

The only explanation that I have seen in textbooks is that since the outer spherical shell is symmetrical relative to internal charged spherical shell so field every where on the outer shell is same in magnitude at every point on it.

I can understand that electric field needs to be perpendicular to the outer spherical surface since no component parallel to the spherical surface can exist when charges are static i.e. charges are not moving.

But I still cannot get why symmetry makes the magnitude of electric field the same at all points on the imaginary outer spherical shell.

 

[hutchphd]

The outer shell needs to be a ~conductor for this to happen spontaneously. There will be forces (or to put it equivalently the charges will seek lowest energy solution...this presumes some small damping mechanism). If there is asymmetry, there will be forces

 

[vcsharp2003]

The outer shell needs to be a ~conductor for this to happen spontaneously. There will be forces (or to put it equivalently the charges will seek lowest energy solution...this presumes some small damping mechanism). If there is asymmetry, there will be forces

But why is electric field having same magnitude at all points on the imaginary outer spherical shell? Your answer doesn't explain it.

 

[hutchphd]

$\nabla \cdot {\vec E}=\frac \rho {\epsilon_0}$

 

[vcsharp2003]

$\nabla \cdot {\vec E}=\frac \rho {\epsilon_0}$

This equation would be Gauss's law
for an infinitesimal area on the outer imaginary spherical shell. How can we now conclude that all points on outer shell have same magnitude of E?

 

[Steve4Physics]

I can understand that electric field needs to be perpendicular to the outer spherical surface since no component parallel to the spherical surface can exist when charges are static i.e. charges are not moving.

But I still cannot get why symmetry makes the magnitude of electric field the same at all points on the outer spherical shell.

See if this helps...

Call the centre of the system O and consider any two points, P and Q, on the outer shell.

Now take an imaginary walk in a straight line from O to P. Measure the magnitude and direction of the electric field relative to your path using your recently purchased electric-field-magnitude-and-direction-measuring-device. Then do the same going from O to Q.

If there is ANY difference between your results for OP and for OQ, the field is not spherically symmetric. There must have been something which made the path OP and OQ different – so you didn’t actually have spherical symmetry.

If the field is truly spherically symmetric, then by definition you will find the magnitudes of the fields at P and Q are equal (and, as you already know, the field directions at P and Q are parallel to OP and to OQ).

If you find $|E_P|$ and $|E_Q|$ are unequal, the system was not spherically symmetric.

 

[vcsharp2003]

See if this helps...

Call the centre of the system O and consider any two points, P and Q, on the outer shell.

Now take an imaginary walk in a straight line from O to P. Measure the magnitude and direction of the electric field relative to your path using your recently purchased electric-field-magnitude-and-direction-measuring-device. Then do the same going from O to Q.

If there is ANY difference between your results for OP and for OQ, the field is not spherically symmetric. There must have been something which made the path OP and OQ different – so you didn’t actually have spherical symmetry.

If the field is truly spherically symmetric, then by definition you will find the magnitudes of the fields at P and Q are equal (and, as you already know, the field directions at P and Q are parallel to OP and to OQ).

If you find $|E_P|$ and $|E_Q|$ are unequal, the system was not spherically symmetric.

This doesn't explain that magnitude is same across all points on outer shell in magnitude.

I am looking for a theoretical explanation of this.

 

[hutchphd]

How's abought this: to be bigger in one spot that another will also require either charge variations or Electric fields parallel to the surface (that's what Maxwell says). The charge will redistribute as soon as that happens to make it not happen, QED.

 

[vcsharp2003]

How's abought this: to be bigger in one spot that another will also require either charge variations or Electric fields parallel to the surface (that's what Maxwell says). The charge will redistribute as soon as that happens to make it not happen, QED.

Electric field is going to be always normal at every point on the outer imaginary shell since charges are in a static position. So, electric field will never have a parallel component on the outer shell. This means if two points on the outer shell have different magnitudes of E then the charges will still not move. Therefore, your explanation doesn't explain why E magnitude is same across all points on the outer imaginary shell.

 

[Delta2]

You are basically asking to explain why the spherical symmetry is a spherical symmetry. Hard to explain this.

Only work around I see is to go to Gauss's law in differential form $\nabla\cdot \vec{E}=\frac{\rho}{\epsilon_0}$ which together with the boundary condition that the field E is zero at infinity, has the general solution $$\vec{E}(\vec{r})=\int \frac{\rho(\vec{r'})(\vec{r}-\vec{r'})}{|\vec{r}-\vec{r'}|^3}d^3\vec{r'}$$.

Then given the spherical uniform charge density $\rho(\vec{r'})$ (which will actually be a surface charge density, not a volume charge density, and the integral will be a surface integral, not a volume integral for this specific example), to calculate the above integral for two points $\vec{r}=\vec{r_A}$ and $\vec{r}=\vec{r_B}$, $|\vec{r_A}|=|\vec{r_B}|$. After long and painful calculation you ll find that $$|\vec{E}(\vec{r_A})|=|\vec{E}(\vec{r_B})|$$

 

[Delta2]

There are some threads here in physics forums where this calculation is done, wait if I can pinpoint you to one.
Check here,
https://www.physicsforums.com/threa...ical-charged-shell-direct-integration.759988/
I think there are many other threads with the same subject.

 

[vcsharp2003]

You are basically asking to explain why the spherical symmetry is a spherical symmetry. Hard to explain this.

Only work around I see is to go to Gauss's law in differential form $\nabla\cdot \vec{E}=\frac{\rho}{\epsilon_0}$ which together with the boundary condition that the field E is zero at infinity, has the general solution $$\vec{E}(\vec{r})=\int \frac{\rho(\vec{r'})(\vec{r}-\vec{r'})}{|\vec{r}-\vec{r'}|^3}d^3\vec{r'}$$.

Then given the spherical uniform charge density $\rho(\vec{r'})$ (which will actually be a surface charge density, not a volume charge density, and the integral will be a surface integral, not a volume integral for this specific example), to calculate the above integral for two points $\vec{r}=\vec{r_A}$ and $\vec{r}=\vec{r_B}$. After long and painful calculation you ll find that $$|\vec{E}(\vec{r_A})|=|\vec{E}(\vec{r_B})|$$

Couldn't we explain it theoretically without calculus in following manner? For each point P on the outer shell, the charges of very small areas on inner shell will result in a bunch of electric field vectors at point P that point outwards forming a cone of outward vectors which will be symmetrical about the point P on outer shell i.e. they will form an inverted cone pattern with its apex at point O. This cone of field vectors will have their components parallel to the outer shell cancel each other leaving only the components pointing outwards perpendicular to the surface at point P on outer shell. This will be same for each point on outer shell. Thus, electric field at every point on outer shell will be along outward normal to spherical shell and the same in magnitude.

 

[Delta2]

Couldn't we say that for each point on outer shell, the charges on all very small areas on inner shell will have a bunch of field vectors that point outwards forming a cone of outward vectors which will be symmetrical about the point on outer shell. This cone of vectors will have their components parallel to the outer shell cancel each other leaving only the components point outwards for the point on outer shell. This will be same for each point on outer shell. Thus, electric field at every point on outer shell will be along outward normal to spherical shell and the same in magnitude.

This seems a rather too much intuitive explanation. You have to do the calculation to prove it.

 

[vcsharp2003]

This seems a rather too much intuitive explanation. You have to do the calculation to prove it.

Your approach seems very rigorous and surely precise. But isn't my theoretical explanation also explaining it? After all, the field at each point on outer shell is a superposition of fields due to infinitesimal charges/areas on inner shell. The cone of vectors is always formed about the point on outer shell since these infinitesimal areas of inner shell are going to be symmetrical in their placements/relative locations for each point on outer shell.

 

[Delta2]

Your approach seems very rigorous and surely precise. But isn't my theoretical explanation also explaining it? After all the field at each point on outer shell is a superposition of fields due to infinitesimal charges/areas on inner shell. The cone of vectors is always formed about the point on outer shell since these infinitesimal areas of inner shell are going to be symmetrical for each point on outer shell.

Yes it explains it but you have to do the math to prove it 100%.

 

[vcsharp2003]

Yes it explains it but you have to do the math to prove it 100%.

Yes, it's not proving it mathematically as you have mentioned.

Actually, this cone of vectors concept can also be used in other electrostatic scenarios like finding the net electric field at point P on the axis of a charged ring as shown in the diagram below. It seems like a useful concept for students who are not into very rigorous proofs.

 

[vcsharp2003]

There are some threads here in physics forums where this calculation is done, wait if I can pinpoint you to one.
Check here,
https://www.physicsforums.com/threa...ical-charged-shell-direct-integration.759988/
I think there are many other threads with the same subject.

Thanks for this link. You provide very clear answers which is a great help. It exactly proves what I have asked in my original question. I will need to look it up in detail to understand it.

 

[vela]

Consider a point P on the imaginary outer sphere. Orient the coordinate axes so P lies on the x-axis. Now consider a point Q elsewhere on the sphere where $E_{\rm P} \ne E_{\rm Q}$. Rotate the system so that point Q now lies on the x-axis. But the charge distribution before and after the rotation is identical because of its spherical symmetry, yet if $E_{\rm P} \ne E_{\rm Q}$, these two identical distributions produce different electric field magnitudes at the point on the x-axis, which can't happen. Therefore, the assumption that $E_{\rm P} \ne E_{\rm Q}$ is invalid.