Mass slipping on a moving inclined plane

[york]

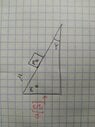
Homework Statement

Hey everyone, i run across this quastion and i don't know hot to find the min and max of a

Relevant Equations

Fk = miu*N

Body A rests on a inclined plane of body B . the angle of slope is α , the coefficient of friction between the two bodies is μ . Body A does not slip on body B because we accelerate body B with a. What is the minimum and maximum acceleration required for body A not to slip? What will be the results if the slope angle α is 0? What will be the results if the slope angle α is 90°?

 

[haruspex]

Per forum rules, you must show some attempt.

 

[york]

you right, sorry.
this is what i did, but i got a expression for a but i don't know how to find the min and max

 

[haruspex]

you right, sorry.
this is what i did, but i got a expression for a but i don't know how to find the min and max

I disagree with your first equation ("N+..."), and with the RHS of the third one. In each case, it's the coefficient of the a term I question.

Re min and max, what may happen if a is too small? What if a is too large?

 

[york]

I disagree with your first equation ("N+..."), and with the RHS of the third one. In each case, it's the coefficient of the a term I question.

Re min and max, what may happen if a is too small? What if a is too large?

if a is too amall the block A will slide down, and if a is too large i think the block will severed from the plane backward

 

[haruspex]

the block will severed from the plane backward

Sorry, I don't know what you mean by that.

What about the errors in the equations? Please explain how you get those terms.