Math Challenge - March 2020

[fresh_42]

Questions

1. (solved by @Antarres, @Not anonymous ) Prove the inequality $\cos(\theta)^p\leq\cos(p\theta)$ for $0\leq\theta\leq\pi/2$ and $0<p<1$. (IR)

2. (solved by @suremarc ) Let $F:\mathbb{R}^n\to\mathbb{R}^n$ be a continuous function such that $||F(x)-F(y)||\geq ||x-y||$ for all $x,y\in\mathbb{R}^n$. Show that $F$ is a homeomorphism. (IR)

3. (solved by @Fred Wright ) Evaluate the integral $\int_0^{\infty}\frac{e^{-t}\sin(t)}{t}dt\,.$ (IR)

4. (solved by @suremarc ) Let $k$ be a field that is not algebraically closed. Let $n\geq 1$. Show that there exists a polynomial $p\in k[x_1,\ldots,x_n]$ that vanishes only at the origin $(0,\ldots,0)\in k^n$. (IR)

5. (solved by @Not anonymous ) Find the area of the shape $T$ which is surrounded by the line $|a_1 x + b_1 y + c_1| + |a_2 x + b_2 y + c_2| = m , m \gt 0$ (given that $a_1 b_2 - a_2 b_1 \neq 0$). (QQ)

6. (solved by @Antarres ) Calculate $I = \iint\limits_{R^2} e^{-|y|- x^2} dx dy$ (QQ)

7. (solved by @Antarres ) Let's take the vector space of continuous real functions. Let also $g: V \ni f \rightarrow g(f) \in V$ be a linear mapping with $(g(f))(x) = \int_{0}^{x} f(t) dt\,.$ Show that $g$ has no eigenvalues. (QQ)

8. Let $\mathfrak{g}=\operatorname{lin}_\mathbb{R}\{\,e_1,e_2,e_3,e_4\,\}$ on which we define the following multiplication:
$$
[e_1,e_4]=2e_1\; , \;[e_2,e_4]=3e_2-e_3\; , \;[e_3,e_4]=e_2+3e_3
$$
and $[e_i,e_j]=0$ otherwise, as well as $[e_i,e_i]=0$.
Show that
a.) $\mathfrak{g}$ is a Lie algebra.
b.) There exists an $\alpha_0 \in A(\mathfrak{g})$ where $$
A(\mathfrak{g}):=\{\,\alpha : \mathfrak{g}\stackrel{\text{linear}}{\longrightarrow} \mathfrak{g}\,|\,\forall\,X,Y \in \mathfrak{g}: [\alpha(X),Y]+[X,\alpha(Y)]=0\,\}
$$
such that $[\operatorname{ad}X,\alpha_0] \in \mathbb{R}\cdot \alpha_0$ for all $X\in \mathfrak{g}\,.$
c.) The center $Z(\mathfrak{g})=\{\,0\,\}\,.$
d.) $\mathfrak{g}$ has a one dimensional ideal.
(FR)

9. (solved by @suremarc ) Let $A,B\in \mathbb{M}(m,\mathbb{R})$ and $\|A\|,\|B\|\leq 1$ with a submultiplicative matrix norm, then $$\left\|\,e^{A+B}-e^A\cdot e^B\,\right\|\leq 6e^2\cdot \left\|\,[A,B]\,\right\|$$
(FR)

10. (solved by @julian ) Show that for $m \times m$ matrices $A,B$
$$
e^{t\,(A+B)} = \lim_{n \to \infty}\left(e^{t\,\frac{A}{n}} \cdot e^{t\,\frac{B}{n}}\right)^n
$$
in a submultiplicative matrix norm.
Hint: You may use the estimation in problem #9. (FR)

High Schoolers only

11. (solved by @etotheipi, @Not anonymous, @lekh2003 ) If $\tan^2 a = 1 + 2 \tan^2 b$ show that it also holds $\cos 2b - 2 \cos 2a = 1$ (QQ)

12. (solved by @etotheipi ) Inside a steel sphere of radius $R$ we construct a spherical cavity which is tangent to the steel sphere and passes through its center ($Fig. 1$). Before this construction, the mass of the steel sphere was $M$. Find the force $F$ (which is due to the Newton's law of gravitation) with which the steel sphere pulls a small sphere of mass $m$ which is at a distance $d$ from its center over the straight line of centers and on the side of the cavity.

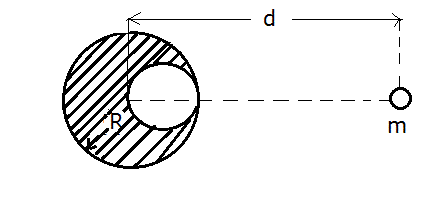
$Fig. 1$

Now, I think this way: I find the center of gravity of the sphere with the cavity: its distance from the center of the sphere I would have without constructing the cavity (i.e. concrete sphere), can be found from the equation $Mgx = \frac{Mg}{8} (\frac{R}{2} + x)$ from which I find $x = \frac{R}{14}$. Then, I find the force $F$ which is exerted on the sphere of mass $m$ by the sphere with the cavity (its mass is the $\frac{7}{8}$ of the mass of the concrete steel sphere), like we had two spheres with a distance $d + \frac{R}{14}$ between them, so $F = G\frac{\frac{8}{7}Mm}{(d + \frac{R}{14})^2}$.

Is this correct? Try to recreate the solution in detail and justify your answer. If the above solution is not correct, give your solution. (QQ)

13. (solved by @Not anonymous ) Let $f:\mathbb{Q}\to\mathbb{Q}$ be the function $f(x)=x^3-2x$. Show that $f$ is injective. (IR)

14. (solved by @Not anonymous, @krns21 ) Given two integers $n,m$ with $nm\neq 0$. Show that there is a integer expression $1=sn+tm$ if and only if $n$ and $m$ are coprime, i.e. have no proper common divisor. (FR)

15. (solved by @Not anonymous ) Division of an integer by a prime number $p$ leaves us with the possible remainders $C:=\{\,0,1,2,\ldots ,p-1\,\}\,.$ We can define an addition and a multiplication on $C$ if we wrap it around $p$, i.e. we identify $0=p=2p=3p= \ldots \, , \,1=1+p=1+2p=1+3p=\ldots\, , \,\ldots$ This is called modular arithmetic (modulo $p$).

Show that for any given numbers $a,b\in C$ the equations $a+x=b$ and $a\cdot x =b$ ($a\neq 0$) have a unique solution.
Is this still true if we drop the requirement that $p$ is prime? (FR)

Remark: This problem is about proof techniques, so be as accurate (not long) as possible, i.e. note which property or condition you use at each step.

 

[krns21]

14. Given two integers $n,m$ with $nm\neq 0$. Show that there is a integer expression $1=sn+tm$ if and only if $n$ and $m$ are coprime, i.e. have no proper common divisor. (FR)

Spoiler: Problem 14

Let gcd$(n,m)=a$
Therefore:
$n=aq$ for some integer $q$
$m=ap$ for some integer $p$
Substituting $aq$ and $aq$ for $n$ and $m$ to the expression $1= sn + tm$, we see that:
$1 =saq + tap$
$1 = a(sq+tp)$
Since all are integers, $sq+tp$ must also be an integer. Therefore, $a=1$.
If $a > 1$, then this expression has no integer solutions for any $s,q,tp$. It's easier seen in this form:
$\frac{1}{a} = sq +tp$
The left hand side of this expression is a fraction whilst the right hand side is integer and so there is a contradiction.

 

[fresh_42]

Spoiler: Problem 14

Let gcd$(n,m)=a$
Therefore:
$n=aq$ for some integer $q$
$m=ap$ for some integer $p$
Substituting $aq$ and $aq$ for $n$ and $m$ to the expression $1= sn + tm$, we see that:
$1 =saq + tap$
$1 = a(sq+tp)$
Since all are integers, $sq+tp$ must also be an integer. Therefore, $a=1$.
If $a > 1$, then this expression has no integer solutions for any $s,q,tp$. It's easier seen in this form:
$\frac{1}{a} = sq +tp$
The left hand side of this expression is a fraction whilst the right hand side is integer and so there is a contradiction.

You have shown, that if we have such an expression, then $n$ and $m$ are coprime:
$1=sn+tm \,\wedge \, a|n \,\wedge \, a|m \Longrightarrow a=1$

Your second argument says $a >1 \,\wedge \, a|n \,\wedge \, a|m\Longrightarrow 1\neq sn+tm$ which is equivalent to the first.

However, if we assume $(n,m)=1$, then you must show that $s$ and $t$ exist with $1=sn+tm\,.$

 

[fresh_42]

Spoiler: Problem 14

Let gcd$(n,m)=a$
Therefore:
$n=aq$ for some integer $q$
$m=ap$ for some integer $p$
Substituting $aq$ and $aq$ for $n$ and $m$ to the expression $1= sn + tm$, we see that:
$1 =saq + tap$
$1 = a(sq+tp)$
Since all are integers, $sq+tp$ must also be an integer. Therefore, $a=1$.
If $a > 1$, then this expression has no integer solutions for any $s,q,tp$. It's easier seen in this form:
$\frac{1}{a} = sq +tp$
The left hand side of this expression is a fraction whilst the right hand side is integer and so there is a contradiction.

A hint: You could consider all natural numbers $x=sn+tm$ and consider what you can find out about the smallest of them.

 

[krns21]

A hint: You could consider all natural numbers $x=sn+tm$ and consider what you can find out about the smallest of them.

Spoiler

Bezout's identity?

 

[krns21]

For Problem 15, if both $a= 0$ and $b= 0$, then $a \cdot x = b$ doesn't have a unique solution.

 

[fresh_42]

For Problem 15, if both $a= 0$ and $b= 0$, then $a \cdot x = b$ doesn't have a unique solution.

Thanks for the hint. Yes, $a\neq 0$ has to be added to the question. I corrected it.

 

[fresh_42]

Spoiler

Bezout's identity?

Yes, but how to prove it? Consider the smallest integer number $x=sn+tm > 0$ and take $1= \operatorname{gcd}(n,m)$. Why is $x=1$?

 

[etotheipi]

Spoiler: Problem 11

$\tan^{2}{(a)} = 1+ 2\tan^{2}{(b)}$
$\sec^{2}{(a)} - 1 = 1+ 2\sec^{2}{(b)} -2 = 2\sec^{2}{(b)} - 1$
$\cos^{2}{(a)} = \frac{1}{2} \cos^{2}{(b)}$
$\frac{\cos{(2a)}+1}{2} = \frac{1}{2} \times \frac{\cos{(2b)}+1}{2}$
$2\cos{(2a)} + 2 = \cos{(2b)}+1 \implies \cos{(2b)} - 2\cos{(2a)} = 1$

 

[etotheipi]

Spoiler: Problem 12

The force on $m$ due to the whole large sphere without the cavity, $F_T$ can be considered as the sum of the forces due to the large sphere with the cavity, $F_C$, and the force due to a spherical mass which fills the cavity, $F_M$, by the principle of superposition.

So $F_C = F_T - F_M$

The force that would result from the whole large sphere without a cavity is $F_T = \frac{GMm}{d^2}$. The force that would result from the spherical mass taking the place of the cavity is $F_M = \frac{GMm}{8(d-\frac{R}{2})^{2}}$.

So $F_C = GMm[\frac{1}{d^{2}} - \frac{1}{8(d-\frac{R}{2})^{2}}]$

For the second part, I think the error lies in abstracting the mass with the cavity to a sphere because the spatial distribution of mass will affect the resulting field.

 

[Not anonymous]

11. If $\tan^2 a = 1 + 2 \tan^2 b$ show that it also holds $\cos 2b - 2 \cos 2a = 1$ (QQ)

Spoiler: Question 11

The proof uses the following identities:
1. $\cos (x+y) = \cos x \cos y - \sin x \sin y \Rightarrow \cos {2A} = \cos {(A+A)} = \cos^2 A - \sin^2 A = 2 \cos^2 A - 1$

2. $\tan x = \frac {\sin x} {\cos x}$

3. $\sin^2 x = 1 - \cos^2 x$

The given equality, $\tan^2 a = 1 + 2 \tan^2 b$, can be rewritten in terms of sine and cosine:
$$
\frac {\sin^2 a} {\cos^2 a} = 1 + 2 \frac {\sin^2 b} {\cos^2 b} \Rightarrow \frac {1} {\cos^2 a} - 1 = 1 + 2 (\frac {1} {\cos^2 b} - 1) \Rightarrow {\cos^2 a} = \frac {\cos^2 b} {2}
$$

Multiplying both sides by 4 and subtracting 2 from both, we get:
$4 \cos^2 a - 2 = 2 \cos^2 b - 2 \Rightarrow 2 (2 \cos^2 a - 1) = (2 \cos^2 b - 1) - 1$

Using the identity for $\cos 2A$ on both sides, the equation becomes
$2 \cos 2a = \cos 2b - 1 \Rightarrow \cos 2b - 2 \cos 2a = 1$, hence proving what is required

 

[lekh2003]

Spoiler: Problem 11

\begin{align*}

\tan^2a &= 1 + 2\tan^2b\\
\tan^2a &= \sec^2b + \tan^2b\\
\cos^2b \tan^2a &= 1 + \sin^2b\\
\cos^2b \tan^2a &= 2 - \cos^2b\\
\cos^2b \sin^2a &= 2\cos^2a - \cos^2b\cos^2a\\
\cos^2b(\sin^2a+\cos^2a) &= 2\cos^2a\\
\cos^2b &= 2\cos^2a\\
\cos^2b &= \cos2a + 1\\
2\cos^2b &= 2\cos2a + 2\\
\cos2b &= 2\cos2a + 1 \\
\implies \cos2b &- 2\cos2a = 1
\end{align*}

Just realized this one was super solved but I'm not going to let this LaTeX go to waste :p

 

[Fred Wright]

Problem #3
I use Feynman's famous trick of differentiation under the integral sign.

Spoiler

$$
\frac {d}{d \alpha} \int_{0}^{ \infty } \frac{e^{-\alpha t}\sin (t)}{t}dt=- \int_{0}^{ \infty }e^{-\alpha t}\sin (t)dt
$$
Integrating by parts:
$$
- \int_{0}^{ \infty }e^{-\alpha t}\sin (t)dt= \frac {1}{\alpha^2 + 1}
$$
taking the antiderivative of $\frac {1}{\alpha^2 + 1}$ :
$$
\int_{0}^{ \infty } \frac{e^{-\alpha t}\sin (t)}{t}dt= atan(\alpha) + C
$$
Setting $\alpha = 0$ to find $C$ :
$$
C= \int_{0}^{ \infty }\frac{\sin (t)}{t}dt
$$
I observe:
$$
\int_{0}^{ \infty }e^{-xt}dt=\frac{1}{x}
$$
and thus (again integrating by parts):
$$
C= \int_{0}^{ \infty }\frac{\sin (t)}{t}dt= \int_{0}^{ \infty } \int_{0}^{ \infty }e^{-xt}\sin (x)dxdt=\int_{0}^{ \infty }\frac{dt}{t^2 + 1}=\frac{\pi}{2}
$$
and finally,
$$
\int_{0}^{ \infty } \frac{e^{- t}\sin (t)}{t}dt= atan(1) + \frac{\pi}{2} = \frac{3 \pi}{4}
$$

 

[lekh2003]

Spoiler: Problem 13

I think I'm far from solving the problem, but I made some progress. I let $$a,b,c,d \in \mathbb{Z}$$ and hence I need to prove $$f\left(\frac{a}{b}\right) = f\left(\frac{c}{d}\right) \implies \frac{a}{b} = \frac{c}{d} \text{ or } ad = bc$$

I managed to simplify this form all the way into:

$$
(ad-bc)((ad)^2 + adbc + (bc)^2) = 2b^2d^2 (ad-bc)
$$

All I need to show now is really that: $$((ad)^2 + adbc + (bc)^2) = 2b^2d^2$$

I'll keep at it.

 

[Infrared]

@Fred Wright Nice work! Your solution is totally correct except for a lost negative sign: $\int_0^{\infty}\frac{e^{-\alpha t}\sin(t)}{t}dt=-\arctan(\alpha)+C.$

So the answer should be $-\pi/4+\pi/2=\pi/4$ instead.

Also, a slightly easier way to find $C$ is to take $\alpha\to\infty.$

 

[QuantumQuest]

Just realized this one was super solved but I'm not going to let this LaTeX go to waste :p

Your solution is correct but you need to correct the latex because at some points there are typos.

 

[lekh2003]

Your solution is correct but you need to correct the latex because at some points there are typos.

Ohhh yeah, I'll do that, thx.

 

[Not anonymous]

14. Given two integers $n,m$ with $nm\neq 0$. Show that there is a integer expression $1=sn+tm$ if and only if $n$ and $m$ are coprime, i.e. have no proper common divisor. (FR)

Spoiler: Question 14

First we prove by contradiction that if $n,m$ are not coprime, then an integer expression of the mentioned form cannot exist. If $n, m$ are not coprime, they must have a GCD $k \gt 1$. $n, m$ can therefore be written as multiples of $k$ with integer quotients, say $a, b$ respectively. Suppose there existed an integers only solution for $1=sn+tm$, then writing $n,m$ in terms of $k$, we get:
$sak + tbk = 1 \Rightarrow k(sa+tb) = 1 \Rightarrow (sa + tb) = \frac 1 k$.
However, since $k \gt 1$, $\frac 1 k$ cannot be an integer and this contradicts the assumption that $s, t, a, b$ are all integers. Hence, such an expression cannot exist for non-coprime numbers $n,m$.

Next we prove that if $n,m$ are coprime, then an integer expression of the form $1=sn+tm$ must exist. For simplicity, we prove this assuming $n,m$ are positive integers. Once that is proved, it is easy to show that a similar expression would exist if negatives of one or both of $n,m$ are used instead. Since if there exist integers $s,t$ such that $sn+tm=1$, then if $n$ is negated (replaced by $-n$), then we simply need to replace $s$ by $-s$ and similarly replace $t$ by $-t$ if $m$ is negated to get the same value for the expression and therefore the existence of an integer-only solution still holds true.

Proof for the case of positive coprime integers $n, m$ is as follows. Since $LCD(n,m) = nm$, $kn \mod m \neq 0$ for any $k \in \{1, 2, ..., m-1\}$. There must exist a $k \in \{1, 2, ..., m-1\}$ for which $kn \mod m = 1$. Suppose there existed no such value of $k$, then the list of $m-1$ values, $(n \mod m, 2n \mod m, 3n \mod m, ..., (m-1)n \mod m)$ must have at least one repeated integer value $p, 1 \lt p \lt m$ (since the list has $(m-1)$ elements and modulo w.r.t. m can only take values from $\{0, 1, .., (m-1)\}$ and 0, 1 have been ruled out as possible values, leaving only $(m-2)$ values to choose from for the $(m-1)$ elements, there must be a repetition). Suppose $k_1, k_2$ (assume $k_1 \lt k_2$) were 2 of the different values of $k$ for which $kn \mod m = p$, then $k_2 n - k_1 n = 0 \mod m \Rightarrow (k_2 - k_1)n = 0 mod m$ and since $1 \leq k_2 - k_1 \lt (m-1)$, this contradicts the requirement that $kn \mod m \neq 0$ for any $k \in \{1, 2, ..., m-1\}$. Hence it is proven that there exists a $k \in \{1, 2, ..., m-1\}$ for which $kn \mod m = 1$. Now, for that value of $k$, we must have $kn = qm +1$ for some integer $q \geq 1$. Hence the expression $kn + (-q)m$ must have the value 1, therefore we have an integer expression $1 = sn + tm$ that is true with $s = k$ and $t = q$. Hence proven.

 

[hilbert2]

For problem 1:

Spoiler

First of all, it's known that

$1-\frac{1}{2}\theta^2 \leq \cos \theta \leq 1-\frac{1}{2}\theta^2 +\frac{1}{24}\theta^4$

and

$1-\frac{1}{2}p^2 \theta^2 \leq \cos p\theta \leq 1-\frac{1}{2}p^2 \theta^2 +\frac{1}{24}p^4 \theta^4$

when $\theta\in [0,\pi /2]$.

Then, if we could show that

$(\cos \theta)^p \leq \left(1-\frac{1}{2}\theta^2 +\frac{1}{24}\theta^4 \right)^p \leq \left(1-\frac{1}{2}p^2 \theta^2\right) \leq \cos p\theta$,

or most importantly, the part

$\left(1-\frac{1}{2}\theta^2 +\frac{1}{24}\theta^4 \right)^p \leq \left(1-\frac{1}{2}p^2 \theta^2\right)$

for $\theta\in ]0 ,\pi/2[$ and $p\in [0,1]$,

then it would prove the claim.

Drawing graphs of the functions $f(\theta) = \left(1-\frac{1}{2}\theta^2 +\frac{1}{24}\theta^4 \right)^p$ and $g(\theta )=\left(1-\frac{1}{2}p^2 \theta^2\right)$ it seems that $f(x)\leq g(x)$ on that interval no matter how small number the $p$ is, but I'm not sure how to actually prove it.

Assuming that $p$ is the reciprocal of an integer: $p = 1/n$ with $n\in\mathbb{N}$, it may be possible to prove this for any $n\in\mathbb{N}$ with mathematical induction.

 

[Antarres]

Spoiler: Question #1

Take the function : $f(\theta) = \cos(p\theta) - \cos^p(\theta)$.
We find the first derivative:
$$f'(\theta) = -p\sin(p\theta) + p\cos^{p-1}(\theta)\sin(\theta)$$
We want to check that $f'$ is nonnegative(because $f(0)=0$), which makes our function increasing on the interval $0\leq\theta\leq \frac{\pi}{2}$, for $0<p<1$.
In order to check this, we analyze the function:
$$g(x) = \cos^{p-1}(\theta)\frac{\sin(\theta)}{\theta}$$
Since $\cos^{p-1}(\theta) = \frac{1}{\cos^{1-p}(\theta)}$ is an increasing function, as a composition of two decreasing functions(cosine is decreasing in the first quadrant), this means that $\cos^{p-1}(\theta) \geq 1$ for $0\leq\theta\leq\tfrac{\pi}{2}$, and hence $g(\theta) \geq 1$ on this interval, since $\frac{\sin(x)}{x}$ is positive on this interval.
Then we have:
$$g(\theta) \geq 1 >p \Rightarrow \cos^{p-1}(\theta)\sin(\theta) > p\theta \geq \sin(p\theta)$$
where in the last inequality we used the known relation $\sin(x) \leq x$ that holds for all $x$.
But then this means that $f'(\theta) >0$, by multiplying the above inequality by $p$. Hence, $f$ is increasing.
For $\theta = 0$, we have $f(0) = 0$, so the function is positive on this interval. So we have:
$$f(\theta) \geq 0 \Rightarrow \cos(p\theta) \geq \cos^p(\theta)$$
This finishes the proof.

 

[Antarres]

This sounds kind of simple, since the integrals are separated...or am I missing something?

Spoiler: Question #6

Denote:
$$I = \iint_{R^2} e^{-\vert y\vert -x^2}dxdy = \int_{-\infty}^{\infty} e^{-\vert y\vert}dy \int_{-\infty}^{\infty} e^{-x^2}dx$$
We solve the integrals separately:
$$\int_{-\infty}^{\infty} e^{-\vert y\vert}dy = 2 \int_0^{\infty} e^{-y}dy =2$$
$$\int_{-\infty}^{\infty} e^{-x^2}dx = \sqrt{\pi}$$

The second integral is Gaussian integral, which can be integrated as follows:
$$ \left(\int_{-\infty}^{\infty} e^{-x^2}dx\right)^2 = \left(\int_{-\infty}^{\infty} e^{-x^2}dx\right)\left(\int_{-\infty}^{\infty} e^{-y^2}dy\right) \equiv I_G^2$$
Switching to polar coordinates, we find:
$$I_G^2 = 2\pi \int_{0}^{\infty} e^{-r^2}rdr = \pi\int_{0}^{\infty} e^{-r^2} d(r^2) = \pi$$
Hence: $I_G = \sqrt{\pi}$
So finally, we find: $I = 2\sqrt{\pi}$

 

[Antarres]

Spoiler: Question #7

We have from definition of $g$, that if $F$ is a primitive function of $f$:
$$g(f) = F \qquad F'(x) = f(x)$$
by fundamental theorem of calculus.
Then, the eigenvalue equation for $g$ is:
$$g(f) = \lambda f$$
for some $\lambda \in \mathbb{R}$. Substituting the first equation into this, we have:
$$F(x) = \lambda F'(x)$$
with $F(0)=0$.
The general solution of this equation is proportional to the exponential function(obtained by separation of variables):
$$F(x) = Ae^{\lambda x}$$
with $A$ being the integration constant. However, the initial condition cannot be satisfied for this function, hence there are no solutions to the initial value problem and so for the eigenvalue problem either.
QED

 

[Infrared]

Since $\cos^{p-1}(\theta) = \frac{1}{\cos^{1-p}(\theta)}$ is an increasing function, as a composition of two decreasing functions(cosine is decreasing in the first quadrant), this means that $\cos^{p-1}(\theta) \geq 1$ for $0\leq\theta\leq\tfrac{\pi}{2}$, and hence $g(\theta) \geq 1$ on this interval, since $\frac{\sin(x)}{x}$ is positive on this interval.

I don't see how you are concluding that $g(\theta)\geq 1$. I agree that $\cos^{p-1}(\theta) \geq 1$ but $\frac{\sin\theta}{\theta}$ is less than one.

Anyway, there is a more direct way to get the result from your expression for $f'(\theta)$.

 

[archaic]

Question 1:

Spoiler

$$\begin{align*}
\frac{d}{dx}\left(\cos(px)-\cos^px\right)&=-p\sin(px)+p\sin x\cos^{p-1}x\\
&=p\left(\sin x\cos^{p-1}x-\sin(px)\right)\\
&=p\left(\sum_{k=0}^\infty\frac{(-1)^k\cos^{p-1}x}{(2k+1)!}x^{2k+1}-\sum_{k=0}^\infty\frac{(-1)^k p^{2k+1}}{(2k+1)!}x^{2k+1}\right)\\
&=p\sum_{k=0}^\infty\left(\frac{(-1)^k}{(2k+1)!}x^{2k+1}\left(\cos^{p-1}x-p^{2k+1}\right)\right)\\
&=p\left(\cos^{p-1}x-p\right)x-\frac{p}{3!}\left(\cos^{p-1}x-p^3\right)x^3+\frac{p}{5!}\left(\cos^{p-1}x-p^5\right)x^5+...
\end{align*}$$
Each $-$ operation yields a positive result as long as the coefficients are positive, but I need to prove that.

 

[Infrared]

$$=p\left(\cos^{p-1}x-p\right)x-\frac{p}{3!}\left(\cos^{p-1}x-p^3\right)x^3+\frac{p}{5!}\left(\cos^{p-1}x-p^5\right)x^5+...$$

Can you explain in some more detail why this sum is nonnegative?

 

[archaic]

Can you explain in some more detail why this sum is nonnegative?

I answered too fast

 

[Antarres]

@Infrared You're right, I don't know why I complicated such a simple thing.

Spoiler: Question #1 - derivative non-negativity proof

We take the form of the derivative $f'(\theta)$:
$$f'(\theta) = p(\cos^{p-1}(\theta)\sin(\theta) - \sin(p\theta))$$
Now we remember that sine is an increasing function in the first quadrant, while cosine is a decreasing one. This means that $\cos^{p-1}(\theta) = \tfrac{1}{\cos^{1-p}(\theta)}$ is an increasing function as a composition of two decreasing functions. Then we have the inequalities(keeping in mind $0<p<1$):
$$\sin(p\theta) \leq \sin(\theta) \qquad \cos^{p-1}(\theta)\geq \cos^{p-1}(0) = 1$$
Substituting into the derivative, we find:
$$f(\theta) \geq p\sin(\theta)(\cos^{p-1}(\theta)-1) \geq p\sin(\theta) \geq 0$$
Hence the derivative is nonnegative and $f$ is monotonously increasing as claimed.

 

[archaic]

13. Let $f:\mathbb{Q}\to\mathbb{Q}$ be the function$f(x)=x^3-2x$. Show that $f$ is injective. (IR)

Incomplete attempt:

Spoiler

Let $p/q$ and $r/s$ be in $\mathbb{Q}$ such that $f(p/q)=f(r/s)$.
$$\begin{align*}
f\left(\frac{p}{q}\right)=f\left(\frac{r}{s}\right)&\Leftrightarrow\left(\frac{p}{q}\right)^3-2\frac{p}{q}=\left(\frac{r}{s}\right)^3-2\frac{r}{s}\\
&\Leftrightarrow \left(\frac{p}{q}\right)^3-\left(\frac{r}{s}\right)^3-2\left(\frac{p}{q}-\frac{r}{s}\right)=0\\
&\Leftrightarrow\left(\frac{p}{q}-\frac{r}{s}\right)\left(\left(\frac{p}{q}\right)^2+\frac{p}{q}\frac{r}{s}+\left(\frac{r}{s}\right)^2\right)-2\left(\frac{p}{q}-\frac{r}{s}\right)=0\\
&\Leftrightarrow\left(\frac{p}{q}-\frac{r}{s}\right)\left(\left(\frac{p}{q}\right)^2+\frac{p}{q}\frac{r}{s}+\left(\frac{r}{s}\right)^2-2\right)=0\\
\end{align*}$$
$$\frac{p}{q}=\frac{r}{s}\text{ or }\left(\frac{p}{q}\right)^2+\frac{p}{q}\frac{r}{s}+\left(\frac{r}{s}\right)^2=2$$
$$\begin{align*}
\left(\frac{p}{q}\right)^2+\frac{p}{q}\frac{r}{s}+\left(\frac{r}{s}\right)^2=2&\Leftrightarrow\left(\frac{p}{q}+\frac{r}{s}\right)^2-\frac{p}{q}\frac{r}{s}=2
\end{align*}$$

 

[BWV]

I am lame at proofs, but could not this be a simpler route to #1?

Spoiler: Spoiler

Take the first three terms of the series expansion:

$cos(n\theta)=1-\frac{n^2\theta ^2}{2}+\frac{n^4\theta ^4}{24}$

$cos(\theta)^n=1-\frac{n\theta ^2}{2}+\frac{1}{24}(3n^2-2n)\theta^4$

as $cos(θ)≥0$ for $0≤θ≤π/2$

for 0<n<1,
$\frac{n^2\theta ^2}{2}<\frac{n\theta ^2}{2}$
(the second negative term for $cos(\theta)^n$ is larger)
and
$\frac{1}{24}(3n^2-2n)\theta^4 <\frac{n^4\theta ^4}{24}$
(the third positive term for $cos(\theta)^n$ is smaller)

 

[Antarres]

@BWV You can't equal the cosine to just a couple of terms of Maclaurin expansion, it's an approximation. And it works for small $\theta$, but here it isn't necessarily small. I think that's the problem with your approach. If you took the whole series, then I don't know how simpler it would be. Or if you made those equalities inequalities. I think it's what archaic and hilbert did in their posts.

Also, the last inequality you provide doesn't work for $0<n<1$.

 

[BWV]

No, the last inequality is good, seems counter-intuitive but (3n^2-2n)<n^4 for 0<n<1
it its also true for n>1 and n<-2

I guess if you could prove every positive term of order n is smaller and every negative term greater for $cos(\theta)^n$ relative to $cos(n\theta)$ that would be valid, but the expansion for $cos(\theta)^n$ is kind of wonky

 

[Antarres]

Oh true, my bad, I drew the function incorrectly. Anyways, what I said stands though, you can't equal cosine to the first three terms in the expansion around zero when the angle can go up to $\frac{\pi}{2}$ radians. You can make an inequality like hilbert did, and go from there.

 

[Infrared]

@Antarres The solution to problem 1 is good!

@BWV Here @Antarres is right. You have to justify why you can throw out all of the higher order terms in the Taylor series.

@archaic You're doing the right type of manipulations. Do you want a hint?

 

[hilbert2]

It's possible that the approach in my post about Problem 1 requires more than 2 or 3 terms in the power series approximations when $p>0.9$. Solving this with the properties of derivatives is certainly a lot easier than using only the polynomial bounds for the trig functions.

 

[QuantumQuest]

This sounds kind of simple, since the integrals are separated...or am I missing something?

Your solution is correct. In order for your solution to be perfect just correct the small typo in the second to last line of your latex.