Math Challenge - March 2021

[fresh_42]

Summary: Lie Algebras, Commutative Algebra, Ordering, Differential Geometry, Algebraic Geometry, Gamma Function, Calculus, Analytic Geometry, Functional Analysis, Units.

1. Prove that all derivations $D:=\operatorname{Der}(L)$ of a semisimple Lie algebra $L$ are inner derivations $M:=\operatorname{ad}(L).$

2. Give four possible non-isomorphic meanings for the notation $\mathbb{Z}_p.$

3. (solved by @Office_Shredder ) Let $T\subseteq (\mathbb{Z}_+^n,\preccurlyeq )$ with the partial natural ordering. Then there is a finite subset $S\subseteq T$ such that for every $t\in T$ exists a $s\in S$ with $s\preccurlyeq t.$
$$
\alpha \preccurlyeq \beta \Longleftrightarrow \alpha_i \leq \beta_i \text{ for all }i=1,\ldots,n
$$

4. (a) Solve the following linear differential equation system:
\begin{align*}
\dot{y}_1(t)=11y_1(t)-80y_2(t)\;&\wedge\;\dot{y}_2(t)=y_1(t)-5y_2(t)\\
y_1(0)=0\;&\wedge\;y_2(0)=0
\end{align*}
(b) Which solutions do $y_1(0)=\pm \varepsilon\;\wedge\;y_2(0)=\pm \varepsilon$ have?
(c) How does the trajectory for $y_1(0)=0.001\;\wedge\;y_2(0)=0.001$ behave for $t\to \infty$?
(d) What will change if we substitute the coefficient $-80$ by $-60$?
(e) Calculate (approximately) the radius of the osculating circle at $t=\pi/12$ for both trajectories with initial condition $\mathbf{y}(0)=(-1,1).$

5. (solved by @bpet ) Consider the ideal $I =\langle x^2y+xy ,xy^2+1 \rangle \subseteq \mathbb{R}[x,y]$ and compute a reduced Gröbner basis to determine the number of irreducible components of the algebraic variety $V(I).$

6. (solved by @benorin ) Define the complex function gamma function as
$$
\Gamma(z):=\lim_{n \to \infty}\dfrac{n!\,n^z}{z(z+1)\cdot\ldots\cdot(z+n)}
$$
and prove
(a) $\Gamma(z)=\displaystyle{\int_0^\infty}e^{-t}\,t^{z-1}\,dt\;;\quad\mathfrak{R}(z)>0$
(b) $\Gamma(z)^{-1}=e^{\gamma z}z\,\displaystyle{\prod_{n=1}^\infty}\left(1+\dfrac{z}{n}\right)e^{-\frac{z}{n}}$
where $\gamma :=\displaystyle{\lim_{n \to \infty}\left(1+\dfrac{1}{2}+\dfrac{1}{3}+\ldots+\dfrac{1}{n}-\log(n)\right)}$ is the Euler-Mascheroni constant.

7. (solved by @benorin) Let $u\, : \,[0,1]\times [a,b]\longrightarrow \mathbb{C}$ be a continuous function, such that the partial derivative in the first coordinate exists everywhere and is continuous. Define
$$
U(\lambda):=\int_a^b u(\lambda,t)\,dt\; , \;V(\lambda):=\int_a^b \dfrac{\partial u}{\partial \lambda}(\lambda,t)\,dt.
$$
Show that $U$ is continuously differentiable and $U'(\lambda)=V(\lambda)$ for all $0\leq \lambda\leq 1.$

8. A cardiod is defined as the trace of a point on a circle that rolls around a fixed circle of the same size without slipping.

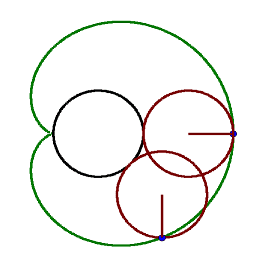
It can be described by $(x^{2}+y^{2})^{2}+4x(x^{2}+y^{2})-4y^{2}\,=\,0$ or in polar coordinates by $r(\varphi )=2(1-\cos \varphi ).$
Show that:

(a) (solved by @etotheipi ) Given any line, there are exactly three tangents parallel to it. If we connect the points of tangency to the cusp, the three segments meet at equal angles of $2\pi/3\,.$

(b) (solved by @etotheipi ) The length of a chord through the cusp equals $4.$
(c) (solved by @etotheipi ) The midpoints of chords through the cusp lie on the perimeter of the fixed generator circle (black one in the first picture).
(d) (solved by @etotheipi ) Calculate length, area and curvature.

9. (solved by @nuuskur ) Let $A$ be a complex Banach algebra with $1$. Prove that the spectrum
$$
\sigma(a)=\{\lambda\in \mathbb{C}\,|\,\lambda\cdot 1-a \text{ is not invertible }\} \subseteq \{\lambda\in \mathbb{C}\,|\,|\lambda|\leq \|a\| \}
$$
for any $a\in A$ is not empty, bounded and closed.

10. (a) Determine all primes which occur as orders of an element from $G:=\operatorname{SL}_3(\mathbb{Z}).$
(b) (solved by @Office_Shredder ) Let $I \trianglelefteq R$ be a two-sided ideal in a unitary ring with group of unities $U$. Show by two different methods that
$$
M:=\{u\in U\,|\,u-1\in I\} \trianglelefteq U
$$
is a normal subgroup.

High Schoolers only (until 26th)11. (solved by @Not anonymous ) If $a,b,c$ are real numbers such that $a+b+c=2$ and $ab+ac+bc=1,$ show that $0\leq a,b,c\leq \dfrac{4}{3}.$

12. Determine all pairs $(m,n)$ of (positive) natural numbers such that $2022^m-2021^n$ is a square.

13. (solved by @archaic , @Not anonymous )
(a) Prove for any $n\in \mathbb{N},\,n\geq 4$
$$
Q(n):=\dfrac{4^2-9}{4^2-4}\cdot\dfrac{5^2-9}{5^2-4}\cdot\ldots\cdot\dfrac{n^2-9}{n^2-4}>\dfrac{1}{6}.
$$
(b) Does the above statement still hold, if we replace $1/6$ on the right hand side by $0.1667\,?$

14. (solved by @Not anonymous ) Determine all pairs $(x,y)\in \mathbb{R}^2$ such that
\begin{align*}
5&=\sqrt{1+x+y}+\sqrt{2+x-y}\\
2-x+y&=\sqrt{18+x-y}
\end{align*}

15. (solved by @Not anonymous ) Given a real, continuous function $f:\mathbb{R}\longrightarrow \mathbb{R}$ such that $f(f(f(x)))=x.$
Prove that $f(x)=x$ for all $x\in\mathbb{R}.$

 

[suremarc]

2. Give four possible non-isomorphic meanings for the notation Zp.

Well, guess I’ll grab the low-hanging fruit:

Spoiler: Solution: Problem 2

1. The cyclic group of prime order $C_p$,
2. The ring $\mathbb{Z}/p\mathbb{Z}$,
3. The group of units modulo $p$, often written as $(\mathbb{Z}/p\mathbb{Z})^\times$,
4. The ring of $p$-adic integers.

Note that $(1)$ and $(3)$ are non-isomorphic (in particular, $(\mathbb{Z}/p\mathbb{Z})^\times\leqslant C_{p-1}$).

I think $(1)$ probably comes from the additive group of elements of $\mathbb{Z}/p\mathbb{Z}$. In fact, I suppose that the notation $\mathbb{Z}_p$ in this case refers to the concrete group $(\mathbb{Z}/p\mathbb{Z})^+$ rather than the abstract group $C_p$ defined by its order. Of course, these are isomorphic as groups — is $C_p$ even a group, and not an isomorphism class thereof? — but perhaps it is more useful in certain contexts to make use of the concrete group.

The only case I can recall where I saw $(1)$ being used was in the definition of a superalgebra: a $\mathbb{Z}_2$-graded algebra.

It would be a pleasant surprise to me if there were other meanings; I don’t know of any others.

 

[fresh_42]

Well, guess I’ll grab the low-hanging fruit:

Spoiler: Solution: Problem 2

1. The cyclic group of prime order $C_p$,
2. The ring $\mathbb{Z}/p\mathbb{Z}$,
3. The group of units modulo $p$, often written as $(\mathbb{Z}/p\mathbb{Z})^\times$,
4. The ring of $p$-adic integers.

Note that $(1)$ and $(3)$ are non-isomorphic (in particular, $(\mathbb{Z}/p\mathbb{Z})^\times\leqslant C_{p-1}$).

I think $(1)$ probably comes from the additive group of elements of $\mathbb{Z}/p\mathbb{Z}$. In fact, I suppose that the notation $Z_p$ in this case refers to the concrete group $(\mathbb{Z}/p\mathbb{Z})^+$ rather than the abstract group $C_p$ defined by its order. Of course, these are isomorphic as groups — is $C_p$ even a group, and not an isomorphism class thereof? — but perhaps it is more useful in certain contexts to make use of the concrete group.

The only case I can recall where I saw $(1)$ being used was in the definition of a superalgebra: a $\mathbb{Z}_2$-graded algebra.

It would be a pleasant surprise to me if there were other meanings; I don’t know of any others.

(1) and (2) are the same ring here. So (1) and (4) are correct. The units of $\mathbb{Z}_p$ are not written that way. At best it would be $\mathbb{Z}_{p-1}$.

Thus two solutions are still missing. But I admit that they would possibly be $\mathbb{Z}_{(p)}$ for some authors.

 

[suremarc]

(1) and (2) are the same ring here. So (1) and (4) are correct. The units of $\mathbb{Z}_p$ are not written that way. At best it would be $\mathbb{Z}_{p-1}$.

Thus two solutions are still missing. But I admit that they would possibly be $\mathbb{Z}_{(p)}$ for some authors.

(1) is not a ring. Are you asking for four non-isomorphic rings? If so, I think this should be stated in the question.

I was also iffy on (3), but Wikipedia says the notation is used outside of number theory. So I thought it was worth a shot.

 

[fresh_42]

(1) is not a ring. Are you asking for four non-isomorphic rings? If so, I think this should be stated in the question.

We can count $\mathbb{Z}_p$ as group, $\mathbb{Z}-$module, ring, associative algebra, Lie algebra, Jordan algebra, field, vector space, tensor algebra. This would be nine structures, but they are all the same, only with more or less operations.

 

[martinbn]

I suppose for the second question one needs to give references, otherwise I can say that I use $\mathbb Z_p$ to denote real numbers, which of course wouldn't count. If the notation $\mathbb Z_{(p)}$ is allowed, then do localizations count?

 

[PeroK]

Is there something missing from question 15?

 

[lekh2003]

I think I'm close on Question 11, but I think I may have done something wrong?

Spoiler: Question 11

$$a(b+c) + bc = 1$$
$$2a-a^2+bc=1$$
The same can be done for the other variables. Then, these equations can be combined.
$$2(a+b+c) - a^2 - b^2 - c^2 + 1= 3$$
Substituting given information:
$$a^2 + b^2 + c^2 = 2$$
This is equivalent to:
$$a^2 + b^2 + c^2 = a + b + c$$
This is a sphere, specifically:
$$\left(a-\frac12\right)^2+\left(b-\frac12\right)^2+\left(c-\frac12\right)^2 = \frac34$$
Here comes my concern. Obviously now I have a set of solutions, that are bounded, and I know information about this because it's a sphere. So, at extreme values of a, b, c can actually reach $\frac12 \pm \frac{\sqrt3}{4}$. This breaks the given bounds right? Did I mess up a calculation?

Am I misinterpreting the condition? Does it imply that if a and b are bounded by those constraints, c must also be bounded. Or that a, b, c all must always be within the bounds regardless of the conditions? I am confus.

 

[Office_Shredder]

I didn't check your work carefully Lekh, but

Spoiler

Your new equation can't be a full description of the solutions since a+b+c=2 is a plane that can't fully contain that sphere. So you've thrown away information about the constraints.

 

[fresh_42]

Is there something missing from question 15?

Oops! Corrected, thanks.

 

[fresh_42]

I think I'm close on Question 11, but I think I may have done something wrong?

Spoiler: Question 11

$$a(b+c) + bc = 1$$
$$2a-a^2+bc=1$$
The same can be done for the other variables. Then, these equations can be combined.
$$2(a+b+c) - a^2 - b^2 - c^2 + 1= 3$$
Substituting given information:
$$a^2 + b^2 + c^2 = 2$$
This is equivalent to:
$$a^2 + b^2 + c^2 = a + b + c$$
This is a sphere, specifically:
$$\left(a-\frac12\right)^2+\left(b-\frac12\right)^2+\left(c-\frac12\right)^2 = \frac34$$
Here comes my concern. Obviously now I have a set of solutions, that are bounded, and I know information about this because it's a sphere. So, at extreme values of a, b, c can actually reach $\frac12 \pm \frac{\sqrt3}{4}$. This breaks the given bounds right? Did I mess up a calculation?

Am I misinterpreting the condition? Does it imply that if a and b are bounded by those constraints, c must also be bounded. Or that a, b, c all must always be within the bounds regardless of the conditions? I am confus.

You have shown $a,b,c < 1.37$ and $1.33$ was the goal. That's close. The missing margin lies in the last equation: $a,b,c$ cannot simultaneously lie in $\left[\dfrac{4}{3},\dfrac{1}{2}+\dfrac{\sqrt{3}}{2}\right].$ What happens in case one equals this limit? Will you need negative values for the other two?

Your estimation is correct. It is simply not the best one.

Edit: You have proven that the given conditions (C) and the sphere (S) are equivalent to (C). From there we cannot conclude that there isn't a property interval (I) which is also equivalent to (C). In formulas:
$$
(\;(C) \wedge (S) \Longleftrightarrow (C)\;) \nRightarrow \nexists (I)\, : \,(\;(C) \wedge (I) \Longleftrightarrow (C)\;)
$$Hint: Get rid of $c$ and solve your second equation.

 

[nuuskur]

Liouville, where art thou?!

Spoiler: Prelims

Spoiler: Proposition

If $\|a\|<1$, then $1-a\in \mathrm{inv}(A)$.

Pf. Put $x_n := \sum _{k=1}^n a^k,\ n\in\mathbb N$. It converges due to $\|a\|<1$.Then for every $n$
$$(1-a)x_n = 1-a^{n+1} = x_n(1-a).$$
Thus, $(1-a) \lim x_n = 1 = \lim x_n(1-a)$.

Spoiler: Lemma

The subset $\mathrm{inv}(A)$ of invertibles is open.
Pf. $1\in\mathrm{inv}(A)$. Let $a\in \mathrm{inv}(A)$. Take $x\in A$ such that $\|x\| < \|a^{-1}\|^{-1}$. Then $\|a^{-1}x\| < 1$. By Prop. $a-x = a(1-a^{-1}x) \in \mathrm{inv}(A)$. Therefore, $B(a, \|a^{-1}\|^{-1}) \subseteq \mathrm{inv}(A)$.

Spoiler: Problem 9 - non-empty

Suppose for a contradiction $\sigma (a) = \emptyset$. Take $\phi\in A'$ and put
$$f:\mathbb C\to \mathbb C,\quad \gamma\mapsto \phi((a-\gamma\cdot 1)^{-1}).$$
This is entire. One can work out the derivative of $\gamma\mapsto (a-\gamma\cdot 1)^{-1}$ to be $(a-\gamma\cdot 1)^{-2}$. For $|\gamma| > \|a\|$ we have $\|\gamma ^{-1}a\|<1$ and
$$\begin{align*} \left\| (a-\gamma \cdot 1)^{-1} \right\| &= \left \| \left (-\gamma(1-\gamma^{-1}\cdot a)\right )^{-1} \right\| \\ &= \left\| (-\gamma)^{-1}\sum (\gamma^{-1}\cdot a)^k \right\| \\ &\leqslant |\gamma|^{-1} \sum \left \|\gamma^{-1}\cdot a \right\|^k \\ &= \frac{1}{|\gamma|} \cdot \frac{1}{1-|\gamma|^{-1}\|a\|} \\ &= \frac{1}{|\gamma|-\|a\|} \xrightarrow[|\gamma|\to\infty]{}0. \end{align*}$$
Thus, $f=0$ by Liouville and since $\phi$ was arbitrary, we conclude $(a-\gamma\cdot 1)^{-1} = 0$, which is impossible.

Spoiler: Problem 9 - compact

Consider $\phi :\mathbb C\to A,\quad \gamma \mapsto a-\gamma \cdot 1$. It is continuous and $\phi ^{-1}(\mathrm{inv}(A)) = \mathbb C\setminus \sigma (a)$, thus $\sigma (a)$ is closed. Take $\lambda \in \sigma (a)$ and assume $|\lambda|>\|a\|$. Then $\|\lambda ^{-1}a\|< 1$ and $a-\lambda \cdot 1 = -\lambda (1-\lambda ^{-1}a) \in\mathrm{inv}(A)$. So the spectrum must be bounded by $\|a\|$.

Funnily enough, the spectral theory works much more nicely in the complex case. In the real case it can be a...real.. nightmare sometimes. One problem is, the spectrum CAN be empty in the real case, e.g take a matrix with characteristic equation $x^2+1 = 0$..

 

[benorin]

6. Define the complex function gamma function as
$$
\Gamma(z):=\lim_{n \to \infty}\dfrac{n!\,n^z}{z(z+1)\cdot\ldots\cdot(z+n)}
$$
and prove
(a) $\Gamma(z)=\displaystyle{\int_0^\infty}e^{-t}\,t^{z-1}\,dt\;;\quad\mathfrak{R}(z)>0$
(b) $\Gamma(z)^{-1}=e^{\gamma z}z\,\displaystyle{\prod_{n=1}^\infty}\left(1+\dfrac{z}{n}\right)e^{-\frac{z}{n}}$
where $\gamma :=\displaystyle{\lim_{n \to \infty}\left(1+\dfrac{1}{2}+\dfrac{1}{3}+\ldots+\dfrac{1}{n}-\log(n)\right)}$ is the Euler-Mascheroni constant.

This work I have copy+pasted from my insight article, A Path to Fractional Integral Representations of Some Special Functions.

(a)
Theorem 1.2: Gamma Function Integral
(Euler 1730): $\Gamma ( z ) = \int_{0}^{\infty} e^{ - t}t^{z - 1} dt , \, \Re \left[ z \right] > 0$
Proof:
\begin{eqnarray*} \Gamma \left( z \right) &:=& \mathop {\lim }\limits_{\lambda \to \infty } \frac{{\lambda !{\lambda ^{z - 1}}}}{{z\left( {z + 1} \right) \cdots \left( {z + \lambda - 1} \right)}} \\&=& \mathop {\lim }\limits_{\lambda \to \infty } \frac{\lambda ! \lambda ^{z - 1}}{z ( z + 1 ) \cdots ( z + \lambda - 2)}\int_{0}^{1} (1-x)^{z + \lambda - 2} dx\end{eqnarray*}
Now, integrate by parts to get
\begin{eqnarray*}\Gamma ( z) &=& \mathop {\lim }\limits_{\lambda \to \infty } \frac{\lambda ! \lambda ^{z - 1}}{z (z + 1) \cdots ( z + \lambda - 2 )}\left\{ \left[ \left. x ( 1 - x) ^{z + \lambda - 2} \right| \right._{x = 0}^1 + \left( {z + \lambda - 2} \right)\int_{0}^{1} x (1 - x)^{z + \lambda - 3}dx\right\} \\ &=& \mathop {\lim }\limits_{\lambda \to \infty } \frac{\lambda !\lambda ^{z - 1}}{z ( z + 1) \cdots ( z + \lambda - 3 ) } \int_{0}^{1} x (1-x) ^{z + \lambda - 3} dx\end{eqnarray*}
In general, k iterations of integration by parts gives
$$\Gamma (z) = \mathop {\lim }\limits_{\lambda \to \infty } \frac{\lambda !\lambda ^{z - 1}}{z(z + 1) \cdots ( z + \lambda - k - 2 ) k!}\int_{0}^1 ( 1 - x)^{z + \lambda - k - 2} x^k dx $$
in particular, $\left( {\lambda - 1} \right)$ iterations of integration by parts gives
$$\Gamma ( z ) = \mathop {\lim }\limits_{\lambda \to \infty } \, \, \lambda ^{z - 1} \int_{0}^{1} ( 1 - x)^{z - 1} x^{\lambda - 1} dx $$
Substitute ${x^\lambda } = y \Rightarrow \lambda {x^{\lambda - 1}}dx = dy$ , to get
$$\Gamma ( z ) = \mathop {\lim }\limits_{\lambda \to \infty } \lambda ^{z - 1} \int_{0}^{1} \left( 1 - y^{\frac{1}{\lambda }} \right) ^{z - 1} dy $$
Set $\lambda = \frac{1}{\eta }$ , so that $\eta \to {0^ + }$ as $\lambda \to \infty$ and
$$\Gamma (z) = \mathop {\lim }\limits_{\eta \to {0^{+}}} \int_{0}^{1} \left( \frac{1 - y^{\eta }}{\eta } \right) ^{z - 1} dy \,\mathop = \limits^H \,\;\int_{0}^{1} {\log }^{z - 1}\left( \frac{1}{y} \right) dy $$
where $\mathop = \limits^H$ denotes the use of L’Hospital’s Rule. Substitute $y={e^{-t}} \Rightarrow dy = - {e^{-t}}dt$ , to get
$$\Gamma \left( z \right) = \;\int_{0}^\infty e^{ - t}t^{z - 1} dt$$
and the theorem is demonstrated.(b)
Weierstrass took as the definition of the gamma function it’s canonical infinite product representation, the so-called Weierstrass product form of the gamma function. The desired representation of the gamma function is here obtained as a corollary to the Weierstrass Factor Theorem‡, the proof of which shall not be reproduced here[2].
Theorem 1.3: Weierstrass Factor Theorem
(Weierstrass): Let $f(z)$ be an entire (i.e. everywhere analytic) function with simple zeroes at $z = a_1,a_2,a_3,\ldots$ where $0 < \left| {{a_1}} \right| < \left| a_2\right| < \left| a_3\right| < \ldots$ and $\mathop {\lim }\limits_{M \to \infty}\;{a_M} =\infty$, then
$$f\left( z \right) = f\left( 0 \right){e^{\frac{{f'\left( 0 \right)}}{{f\left( 0 \right)}}z}}\prod\limits_{k = 1}^\infty {\left[ {\left( {1 - \frac{z}{{{a_k}}}} \right){e^{\frac{z}{{{a_k}}}}}}\right]}$$
The Weierstrass product form of the gamma function is then given by
Corollary 1.4: Weierstrass Product Form of the Gamma Function
(Weierstrass): $\frac{1}{{\Gamma \left( z \right)}} = z{e^{\gamma z}}\prod\limits_{\lambda = 1}^\infty {\left[ {\left( {1 + \frac{z}{\lambda }} \right){e^{ - \frac{z}{\lambda }}}} \right]}$ where $\gamma$ is Euler’s Constant.[3]
Proof:
Let $f\left( z \right) = \frac{1}{{\Gamma \left( {z + 1} \right)}}$ so that f(z) is an entire function with simple zeroes at $z = {a_k}: = - k, \forall k \in {\mathbb{Z}^ + }$ satisfying the hypotheses necessary to invoke Theorem 1.2, which yields
$$\frac{1}{{\Gamma \left( {z + 1} \right)}} = {e^{f'\left( 0 \right)z}}\prod\limits_{k = 1}^\infty {\left[ {\left( {1 + \frac{z}{k}} \right){e^{ - \frac{z}{k}}}} \right]} $$
Set $z=1$ in the above formula and take natural logarithms of the result to determine
\begin{eqnarray*} f^{\prime} (0) &=& \sum_{k = 1}^\infty \left[ \frac{1}{k} - \log \left( 1 + \frac{1}{k} \right) \right] \\&=& \mathop {\lim }\limits_{M \to \infty } \,\sum_{k = 1}^M \left[ \frac{1}{k} + \log ( k ) - \log ( k + 1) \right] \\&=& \mathop {\lim }\limits_{M \to \infty } \,\left[ H_M - \log ( M + 1) \right] +\log 1\\&=& \mathop {\lim }\limits_{M \to \infty } \,\left[ H_M - \log (M + 1) \right] + \underbrace{\mathop {\lim }\limits_{M \to \infty } \log \left( 1 + \frac{1}{M} \right) }_{ = \log 1}\\&=& \mathop {\lim }\limits_{M \to \infty } \,\left( H_M- \log M \right) = :\gamma \end{eqnarray*}
Where $H_M$ is the $\text{M}^{th}$ harmonic number and theorem is proved upon applying Equation 1.1 and replacing $f'\left( 0 \right)$ with $\gamma$ , which is Euler’s Constant. Euler’s constant to four decimal places is
$$\gamma : = \mathop {\lim }\limits_{M \to \infty } \left[ {\sum\limits_{k = 1}^M {\left( {\frac{1}{k}} \right) - \ln M} } \right] = 0.5772 \ldots $$

 

[benorin]

7. Let $u\, : \,[0,1]\times [a,b]\longrightarrow \mathbb{C}$ be a continuous function, such that the partial derivative in the first coordinate exists everywhere and is continuous. Define
$$
U(\lambda):=\int_a^b u(\lambda,t)\,dt\; , \;V(\lambda):=\int_a^b \dfrac{\partial u}{\partial \lambda}(\lambda,t)\,dt.
$$
Show that $U$ is continuously differentiable and $U'(\lambda)=V(\lambda)$ for all $0\leq \lambda\leq 1.$

$$\begin{gathered} \tfrac{dU}{d\lambda}:=\lim_{\Delta \lambda\to 0}\tfrac{\Delta U(\lambda)}{\Delta \lambda} =\int_a^b \lim_{\Delta \lambda\to 0}\tfrac{u(\lambda + \Delta \lambda,t) - u(\lambda ,t)}{\Delta \lambda} \,dt = \int_a^b\tfrac{\partial u}{\partial \lambda }\left( \lambda , t\right)\, dt =: V( \lambda ) \\ \end{gathered}$$

assuming that $a,b$ do not depend on neither $\lambda$ nor $t$. The function defined by the integral over a fixed interval $a\leq t \leq b$ of a continuous function of $0\leq \lambda \leq 1$ which also exists everywhere is continuous, hence $U$ is continuously differentiable.

 

[fresh_42]

I knew I would have regretted that one. Well, I wanted to see the $\varepsilon -\delta$ version without hand waving interchange of integral and limit, or non-transparent argument about continuity.

So here it is for all who are still learning:

Let $\varepsilon>0.$ We have to show that there is a $\delta>0$ such that for all $\lambda,h\in\mathbb{R}$ with $0<|h|<\delta,\,0\leq \lambda\leq 1,$ and $0\leq \lambda+h\leq 1$
$$
\left|V(\lambda+h)-V(\lambda)\right|<\varepsilon\, , \,\left|\dfrac{U(\lambda+h)-U(\lambda)}{h}-V(\lambda)\right|<\varepsilon.
$$
Every continuous function on a compact interval is uniformly continuous, hence there is a $\delta>0$ such that for all $(\lambda,t),(\lambda',t')\in[0,1]\times[a,b]$
$$
|\lambda'-\lambda|+|t'-t|<\delta\Longrightarrow\left|\dfrac{\partial u}{\partial \lambda}(\lambda',t')-\dfrac{\partial u}{\partial \lambda}(\lambda,t)\right|<\dfrac{\varepsilon}{b-a}.
$$
By definition of $V$ we have
\begin{align*}
\left|V(\lambda+h)-V(\lambda)\right|&=\left|\int_a^b\left(\dfrac{\partial u}{\partial \lambda}(\lambda+h,t)-\dfrac{\partial u}{\partial \lambda}(\lambda,t)\right)\,dt\right|\\
&\leq \int_a^b\left|\dfrac{\partial u}{\partial \lambda}(\lambda+h,t)-\dfrac{\partial u}{\partial \lambda}(\lambda,t)\right| \,dt\\
&<\varepsilon
\end{align*}
since the integrand is continuous and takes its maximum in $[a,b].$

Now assume $0<h<\delta$ such that $0\leq \lambda<\lambda+h\leq 1.$ (The case $h<0$ is proven accordingly.) Therefore
\begin{align*}
\left|\dfrac{u(\lambda+h,t)-u(\lambda,t)}{h}-\dfrac{\partial u}{\partial \lambda}(\lambda,t)\right|&=\left|\dfrac{1}{h}\int_{\lambda}^{\lambda+h}\left(\dfrac{\partial u}{\partial \lambda}(\lambda',t)-\dfrac{\partial u}{\partial \lambda}(\lambda,t)\right)d\lambda' \right|\\
&\leq \dfrac{1}{h}\int_{\lambda}^{\lambda+h}\left|\dfrac{\partial u }{\partial\lambda}(\lambda',t)-\dfrac{\partial u}{\partial\lambda}(\lambda,t)\right|d\lambda'\\
&<\dfrac{\varepsilon}{b-a}
\end{align*}
and so
\begin{align*}
\left|\dfrac{U(\lambda+h)-U(\lambda)}{h}-V(\lambda)\right|&=\left|\int_a^b\left(\dfrac{u(\lambda+h,t)-u(\lambda,t)}{h}-\dfrac{\partial u}{\partial \lambda}(\lambda,t)\right)dt\right|\\
&\leq \int_a^b\left|\dfrac{u(\lambda+h,t)-u(\lambda,t)}{h}-\dfrac{\partial u}{\partial \lambda}(\lambda,t)\right|dt\\
&< \int_a^b\dfrac{\varepsilon}{b-a}\,dt = \varepsilon
\end{align*}

 

[benorin]

@fresh_42 what about #6?

 

[fresh_42]

@fresh_42 what about #6?

What do you mean? My proof is basically the same, only written a bit shorter and backwards.

 

[benorin]

@fresh_42 what about #6?
Sorry if this is the second time you see this post: went back hours later to not find my prompting about #6) post (vanished).

 

[fresh_42]

@fresh_42 what about #6?
Sorry if this is the second time you see this post: went back hours later to not find my prompting about #6) post (vanished).

Again: What are you talking about?

Here is your post
https://www.physicsforums.com/threads/math-challenge-march-2021.1000319/#post-6464314

and here are your credits, since at least four hours now.

 

[benorin]

Sorry that last post I made twice from my phone because the second time the first post did not appear on the page after a refresh. My bad, I bugged you twice. Sorry. @fresh_42

 

[docnet]

8. A cardiod is defined as the trace of a point on a circle that rolls around a fixed circle of the same size without slipping.It can be described by $(x^{2}+y^{2})^{2}+4x(x^{2}+y^{2})-4y^{2}\,=\,0$ or in polar coordinates by $r(\varphi )=2(1-\cos \varphi ).$
Show that:

(a) Given any line, there are exactly three tangents parallel to it. If we connect the points of tangency to the cusp, the three segments meet at equal angles of $2\pi/3\,.$
(b) The length of a chord through the cusp equals $4.$
(c) The midpoints of chords through the cusp lie on the perimeter of the fixed generator circle (black one in the first picture).
(d) Calculate length, area and curvature.

I would humbly like to mention problems $8(a)$, $8(b)$ and $8(c)$ are worth another look, and maybe a re-phrasing.

$8(a)$ The claim "given any line...three segments meet at equal angles of $\frac{2\pi}{3}$" is false. If we take a horizontal line, one of three points of tangency is the cusp, we have only two line segments that meet at an angle of $\frac{2\pi}{3}$

$8(b)$ The length of a chord through the cusp equals $4$ for $\phi=(2n+1)\pi$. But, its length does not equal $4$ for $\phi\in R\backslash (2n+1)\pi$, where $n$ is an integer.

$8(c)$ The midpoints of chords through the cusp lie on the perimeter of the black circle for $\phi\in n\pi$ where $n$ is an integer. But, not for all $\phi$. Also, if a line through a cusp intersects the carotid at 3 places, is it still called a chord?

edited for $8(a)$

 

[etotheipi]

Spoiler: Pr 4

I guess I can try this one...

4. (a) Solve the following linear differential equation system:
\begin{align*}
\dot{y}_1(t)=11y_1(t)-80y_2(t)\;&\wedge\;\dot{y}_2(t)=y_1(t)-5y_2(t)\\
y_1(0)=0\;&\wedge\;y_2(0)=0
\end{align*}
(b) Which solutions do $y_1(0)=\pm \varepsilon\;\wedge\;y_2(0)=\pm \varepsilon$ have?
(c) How does the trajectory for $y_1(0)=0.001\;\wedge\;y_2(0)=0.001$ behave for $t\to \infty$?
(d) What will change if we substitute the coefficient $-80$ by $-60$?
(e) Calculate (approximately) the radius of the osculating circle at $t=\pi/12$ for both trajectories with initial condition $\mathbf{y}(0)=(-1,1).$

For $y_1(0) = y_2(0) = 0$, $y_1(t) = y_2(t) = 0$ is a solution. Then given $(\dot{y}_1, \dot{y}_2) = (ay_1 + by_2, cy_1 + dy_2)$, differentiating the second equation and putting it back into the first gives you
$$\ddot{y}_1(t) - (a+d) \dot{y}_1(t) + (ad-bc) y_1(t) = 0$$For $b = -80$ you get a complementary equation $\lambda^2 - 6\lambda + 25 = 0$ which means$$y_1(t) = e^{3t}(A\sin{4t} + B\cos{4t})$$and because $y_2(t) = \frac{1}{b} \dot{y}_1(t) - \frac{a}{b} y_1(t)$, that also gives$$y_2(t) = \frac{e^{3t}}{20} ( (2A + B)\sin{4t} + (2B - A) \cos{4t})$$For initial conditions $(y_1(0), y_2(0)) = (p,q)$ you get $B = p$ and $A = 2p - 20q$, i.e.$$\begin{align*}
y_1(t) &= e^{3t} ( (2p - 20q) \sin{4t} + p \cos{4t}) \\

y_2(t) &= \frac{e^{3t}}{20}((5p - 40q)\sin{4t} + 20q \cos{4t})

\end{align*}$$for $p = q = 0.001$ is just oscillatory with $e^{3t}$ and $\frac{1}{20} e^{3t}$ envelope respectively? Anyway now if you change $b = -60$ then instead the complementary equation gives $\lambda = 1,5$ and by the same procedure as before you get$$\begin{align*}
y_1(t) &= Ae^{5t} + Be^t \\
y_2(t) &= \frac{1}{10}Ae^{5t} + \frac{1}{6}B e^t
\end{align*}$$and similarly given $(y_1(0), y_2(0)) = (p,q)$ you get $A = \frac{5}{2} p - 15q$ and $B = \frac{3}{2}(10q - p)$. For the radius of the osculating circle to the first trajectory, first the ICs $\mathbf{y}(0) = (-1,1)$ imply $$\mathbf{y}(t) = e^{3t} (-22\sin{4t} - \cos{4t}, \cos{4t} - \frac{9}{4} \sin{4t})$$you can work out$$\begin{align*}
\dot{y}_1 \left(\frac{\pi}{12} \right) &= -e^{\frac{\pi}{4}} \left(\frac{91}{2} + 31\sqrt{3} \right) \\
\ddot{y}_1 \left(\frac{\pi}{12} \right) &= e^{\frac{\pi}{4}} \left(89 \sqrt{3} - \frac{521}{2}\right) \\
\dot{y}_2 \left(\frac{\pi}{12} \right) &= -\frac{e^{\frac{\pi}{4}}}{4} \left(12 + \frac{43\sqrt{3}}{2} \right) \\
\ddot{y}_2 \left(\frac{\pi}{12} \right) &= -e^{\frac{\pi}{4}} \left( 244+ 33\sqrt{3} \right)

\end{align*}$$then it's possible to calculate$$R = \left| \frac{(\dot{y}_1^2 + \dot{y}_2^2)^{3/2}}{\dot{y_1}\ddot{y}_2 - \dot{y}_2 \ddot{y}_1} \right|$$same procedure for the other one . Anyway hope I didn't f*ck up too much algebra!

 

[etotheipi]

I think for number 8 it's easier to just stay in polar coordinates. Given $y = r\sin{\varphi}$ and $x = r\cos{\varphi}$, you have$$\begin{align*}
\frac{dy}{d\varphi} &= r\cos{\varphi} + \frac{dr}{d\varphi} \sin{\varphi}\\
\frac{dx}{d\varphi} &= -r\sin{\varphi} + \frac{dr}{d\varphi} \cos{\varphi}
\end{align*}$$You can divide these two to get $dy/dx$, and writing $r' := dr/d\varphi$$$\frac{dy}{dx} = \frac{r\cos{\varphi} + r' \sin{\varphi}}{r' \cos{\varphi} - r\sin{\varphi}}$$Given the trajectory $r(\varphi) = 2(1-\cos{\varphi})$, that becomes$$\frac{dy}{dx} = \frac{\sin^2{\varphi} - \cos^2{\varphi} + \cos{\varphi}}{2\sin{\varphi}\cos{\varphi} - \sin{\varphi}} = \frac{\cos{\varphi} - \cos{2\varphi}}{\sin{2\varphi} - \sin{\varphi}}$$Now, choose an arbitrary line with gradient $k$. The points on the trajectory with equal gradient will then satisfy, using the "sum-to-product" relations,$$\sin{\left(\frac{3\varphi}{2}\right)}\sin{\left(\frac{\varphi}{2}\right)} = k \cos{\left(\frac{3\varphi}{2}\right)}\sin{\left(\frac{\varphi}{2}\right)}$$Since the gradient's undefined at $\varphi = 0$ we can ignore that solution, and we're left with$$\varphi = \frac{2}{3} \tan^{-1}{k} + \frac{2n\pi}{3}, \quad n \in \mathbb{Z}$$Or in other words, so long as $k \neq 0$ you get 3 non-zero solutions in the interval $\varphi \in [0, 2\pi]$ which are spaced by $2\pi / 3$ in angle.

For (b), just choose an arbitrary angle $\phi_0$ and its corresponding $\phi' = \phi_0 + \pi$ on the opposite side of the chord through the cusp. Since $r(\phi') = 2(1-\cos{\phi'}) = 2(1+ \cos{\phi_0})$, the length $L$ of the chord is just$$L = r(\phi_0) + r(\phi') = 2(1-\cos{\phi_0}) + 2(1+\cos{\phi_0}) = 4$$I'll try and finish the question later, but I should get on with my actual homework now haha

 

[fresh_42]

Spoiler: Pr 4

I guess I can try this one...
For $y_1(0) = y_2(0) = 0$, $y_1(t) = y_2(t) = 0$ is a solution. Then given $(\dot{y}_1, \dot{y}_2) = (ay_1 + by_2, cy_1 + dy_2)$, differentiating the second equation and putting it back into the first gives you
$$\ddot{y}_1(t) - (a+d) \dot{y}_1(t) + (ad-bc) y_1(t) = 0$$For $b = -80$ you get a complementary equation $\lambda^2 - 6\lambda + 25 = 0$ which means$$y_1(t) = e^{3t}(A\sin{4t} + B\cos{4t})$$and because $y_2(t) = \frac{1}{b} \dot{y}_1(t) - \frac{a}{b} y_1(t)$, that also gives$$y_2(t) = \frac{e^{3t}}{20} ( (2A + B)\sin{4t} + (2B - A) \cos{4t})$$For initial conditions $(y_1(0), y_2(0)) = (p,q)$ you get $B = p$ and $A = 2p - 20q$, i.e.$$\begin{align*}
y_1(t) &= e^{3t} ( (2p - 20q) \sin{4t} + p \cos{4t}) \\

y_2(t) &= \frac{e^{3t}}{20}((5p - 40q)\sin{4t} + 20q \cos{4t})

\end{align*}$$for $p = q = 0.001$ is just oscillatory with $e^{3t}$ and $\frac{1}{20} e^{3t}$ envelope respectively? Anyway now if you change $b = -60$ then instead the complementary equation gives $\lambda = 1,5$ and by the same procedure as before you get$$\begin{align*}
y_1(t) &= Ae^{5t} + Be^t \\
y_2(t) &= \frac{1}{10}Ae^{5t} + \frac{1}{6}B e^t
\end{align*}$$and similarly given $(y_1(0), y_2(0)) = (p,q)$ you get $A = \frac{5}{2} p - 15q$ and $B = \frac{3}{2}(10q - p)$. For the radius of the osculating circle to the first trajectory, first the ICs $\mathbf{y}(0) = (-1,1)$ imply $$\mathbf{y}(t) = e^{3t} (-22\sin{4t} - \cos{4t}, \cos{4t} - \frac{9}{4} \sin{4t})$$you can work out$$\begin{align*}
\dot{y}_1 \left(\frac{\pi}{12} \right) &= -e^{\frac{\pi}{4}} \left(\frac{91}{2} + 31\sqrt{3} \right) \\
\ddot{y}_1 \left(\frac{\pi}{12} \right) &= e^{\frac{\pi}{4}} \left(89 \sqrt{3} - \frac{521}{2}\right) \\
\dot{y}_2 \left(\frac{\pi}{12} \right) &= -\frac{e^{\frac{\pi}{4}}}{4} \left(12 + \frac{43\sqrt{3}}{2} \right) \\
\ddot{y}_2 \left(\frac{\pi}{12} \right) &= -e^{\frac{\pi}{4}} \left( 244+ 33\sqrt{3} \right)

\end{align*}$$then it's possible to calculate$$R = \left| \frac{(\dot{y}_1^2 + \dot{y}_2^2)^{3/2}}{\dot{y_1}\ddot{y}_2 - \dot{y}_2 \ddot{y}_1} \right|$$same procedure for the other one . Anyway hope I didn't f*ck up too much algebra!

I have different coefficients, and a complex solution as the eigenvalues are complex. I have also difficulties to see what answers what and where possible mistakes are, due to lacking calculations. The goal was to examine the trajectories and their stability towards minor changes.

 

[etotheipi]

Okay here's the rest of question 8:

(c) Take a chord at angle $\phi_0$; by symmetry of the figure around $\varphi = 0$ we can just consider the cases when $\phi_0 \in [0, \pi)$. Let the midpoint of the chord be $M$, then using the result of (b) we have$$OM = 2 - r(\phi_0) = 2 - 2(1-\cos{\phi_0}) = 2\cos{\phi_0}$$The directed line segment $\overrightarrow{OM}$ is at an angle $\phi' = \phi_0 + \pi$ to the ray $\varphi = 0$, so $OM = -2\cos{\phi'}$. Hence the point $M$ lies on the circle $r(\varphi) = -2\cos{\varphi}$.

(d) (i) Since $dx = -r\sin{\varphi} d\varphi + \cos{\varphi} dr$ and $dy = r\cos{\varphi} + \sin{\varphi} dr$ the line element satisfies$$dl = \sqrt{dx^2 + dy^2} = \sqrt{r^2 d\varphi^2 + dr^2} = d\varphi \sqrt{r^2 + r_{\varphi}^2}$$That means$$L= \int_0^{2\pi} dl = \int_0^{2\pi} \sqrt{8 - 8\cos{\varphi}} d\varphi = 4 \int_0^{2\pi} \sin \frac{\varphi}{2} d\varphi = 16$$(ii) This is just another integration, given that $dA = \frac{1}{2}r^2 d\varphi$, $$A = \frac{1}{2} \int_0^{2\pi} (1-\cos{\varphi})^2 d\varphi = 2\left[ \frac{3}{2} \varphi - 2\sin{\varphi} + \frac{1}{4} \sin{4\varphi} \right]_{0}^{2\pi} = 6\pi$$(iii) And the final part is just application of the usual formula$$\begin{align*}

R = \frac{(r^2 + r_{\varphi}^2)^{\frac{3}{2}}}{| r^2 + 2r_{\varphi}^2 -r r_{\varphi \varphi}|} &= \frac{(8 - 8\cos{\varphi})^{\frac{3}{2}}}{12 - 12\cos{\varphi}} \\ \\

&= \frac{8^{\frac{3}{2}} 2^{\frac{1}{2}}}{12} \sin{\frac{\varphi}{2}} = \frac{8}{3} \sin{\frac{\varphi}{2}}\end{align*}$$

 

[etotheipi]

I have different coefficients, and a complex solution as the eigenvalues are complex. I have also difficulties to see what answers what and where possible mistakes are, due to lacking calculations. The goal was to examine the trajectories and their stability towards minor changes.

Hmm when I check with WolframAlpha it seems to be the same as what I wrote down. But I wouldn't be surprised if I messed up. I'll check it tomorrow

 

[fresh_42]

Okay here's the rest of question 8:

(c) Take a chord at angle $\phi_0$; by symmetry of the figure around $\varphi = 0$ we can just consider the cases when $\phi_0 \in [0, \pi)$. Let the midpoint of the chord be $M$, then using the result of (b) we have$$OM = 2 - r(\phi_0) = 2 - 2(1-\cos{\phi_0}) = 2\cos{\phi_0}$$The directed line segment $\overrightarrow{OM}$ is at an angle $\phi' = \phi_0 + \pi$ to the ray $\varphi = 0$, so $OM = -2\cos{\phi'}$. Hence the point $M$ lies on the circle $r(\varphi) = -2\cos{\varphi}$.

And why is this the "black" circle? How about a Cartesian representation, since it shows the location of the center, which $r(\varphi )$ does not?

(d) (i) Since $dx = -r\sin{\varphi} d\varphi + \cos{\varphi} dr$ and $dy = r\cos{\varphi} + \sin{\varphi} dr$ the line element satisfies$$dl = \sqrt{dx^2 + dy^2} = \sqrt{r^2 d\varphi^2 + dr^2} = d\varphi \sqrt{r^2 + r_{\varphi}^2}$$That means$$L= \int_0^{2\pi} dl = \int_0^{2\pi} \sqrt{8 - 8\cos{\varphi}} d\varphi = 4 \int_0^{2\pi} \sin \frac{\varphi}{2} d\varphi = 16$$(ii) This is just another integration, given that $dA = \frac{1}{2}r^2 d\varphi$, $$A = \frac{1}{2} \int_0^{2\pi} (1-\cos{\varphi})^2 d\varphi = 2\left[ \frac{3}{2} \varphi - 2\sin{\varphi} + \frac{1}{4} \sin{4\varphi} \right]_{0}^{2\pi} = 6\pi$$(iii) And the final part is just application of the usual formula$$\begin{align*}

R = \frac{(r^2 + r_{\varphi}^2)^{\frac{3}{2}}}{| r^2 + 2r_{\varphi}^2 -r r_{\varphi \varphi}|} &= \frac{(8 - 8\cos{\varphi})^{\frac{3}{2}}}{12 - 12\cos{\varphi}} \\ \\

&= \frac{8^{\frac{3}{2}} 2^{\frac{1}{2}}}{12} \sin{\frac{\varphi}{2}} = \frac{8}{3} \sin{\frac{\varphi}{2}}\end{align*}$$

... and the curvature is the reciprocal of the radius!

 

[fresh_42]

Hmm when I check with WolframAlpha it seems to be the same as what I wrote down. But I wouldn't be surprised if I messed up. I'll check it tomorrow

I haven't checked whether some scaling via the free parameter gives similar solutions. What are your eigenvectors?

 

[etotheipi]

And why is this the "black" circle? How about a Cartesian representation, since it shows the location of the center, which r(φ) does not?

I'm not sure I completely understand what you're after, but let me try . First consider $S^1 \subseteq \mathbb{R}^2$ to be the black circle drawn in the diagram, around which the cardioid will be drawn. Let the centre of the "rolling" circle have a position $\mathbf{x}_c = (2\cos{\varphi}, 2\sin{\varphi})$, and let the angle turned by the "rolling" circle be $\xi = 2\varphi$. Hence the position of the point on the "rolling" circle which is tracing out the cardioid is$$\mathbf{x}_p = (2\cos{\varphi} - \cos{2\varphi}, 2\sin{\varphi} - \sin{2\varphi})$$Now do a coordinate transformation $\mathbf{x}_p' = \mathbf{x}_p - (1,0)$, so that the new origin coincides with the cusp. The norm of this vector satisfies$$\begin{align*}

\lVert \mathbf{x}_p' \rVert^2 &= 6 + 2\cos{2\varphi} - 4\cos{\varphi} - 4\cos{\varphi}(2\cos^2{\varphi} - 1) - 4\sin{\varphi}(2\sin{\varphi} \cos{\varphi}) \\

&= 4 + 4\cos^2{\varphi} - 8 \cos{\varphi} = [2(1-\cos{\varphi})]^2
\end{align*}
$$so that $\lVert \mathbf{x}_p' \rVert = 2(1-\cos{\varphi})$ is the equation of the cardioid. And also in these coordinates, the equation of the original black circle of unit radius is just $r(\varphi) = -2\cos{\varphi}$. It's just because you can e.g. write the Cartesian form$$(x+1)^2 + y^2 = 1 \implies (r\cos{\varphi} + 1)^2 + r^2\sin^2{\varphi} = 1 \implies r = -2\cos{\varphi}$$

 

[etotheipi]

I haven't checked whether some scaling via the free parameter gives similar solutions. What are your eigenvectors?

By this do you mean the functions $e^{(3 \pm 4i)t}$?

 

[fresh_42]

By this do you mean the functions $e^{(3 \pm 4i)t}$?

Yes. And each of the eigenvalues $\lambda_i =3 \pm 4i$ gives an eigenvector $\mathbf{u_i}$ such that
$\mathbf{y}(t)=c_1e^{\lambda_1 t}\mathbf{u_1}+c_2e^{\lambda_2 t}\mathbf{u_2}$ are the solutions.

Part (a) of course doesn't need any calculation.

 

[bpet]

5. Consider the ideal $I =\langle x^2y+xy ,xy^2+1 \rangle \subseteq \mathbb{R}[x,y]$ and compute a reduced Gröbner basis to determine the number of irreducible components of the algebraic variety $V(I).$

ok so the reduced Groebner basis is (x+1) and (y^2-1) obtained from computing y(x^2y+xy)-x(xy^2-1) and reducing several times.

That would mean, if I understand the definitions correctly, there are 3 irreducible components corresponding to y=1, y=-1 and x=-1.

 

[fresh_42]

ok so the reduced Groebner basis is (x+1) and (y^2-1) obtained from computing y(x^2y+xy)-x(xy^2-1) and reducing several times.

That would mean, if I understand the definitions correctly, there are 3 irreducible components corresponding to y=1, y=-1 and x=-1.

Yes, but can you show the way?

 

[Office_Shredder]

For 3

Spoiler

Proof by induction on n, the dimension of the space.

It's clearly true for n=1, just pick the minimum point in T. I'll do an explicit proof for n=2, because it's easier to visualize.Let $(a,b)$ be an arbitrary point in T, and let's include it in S. Every point in T that's not greater than or equal to a point in S lies in one of the following hyperplanes (i.e. lines in two dimensions), either $x=k$ for some $k=1,2,...,a-1$ or $y=k$ for some $k=1,2,...,b-1$. Let $V$ be an arbitrary such hyperplane. Then $T\cap V$ is a subset of a copy of $\mathbb{Z}_+$ and so by the inductive hypothesis there is a subset $S_V \subset T\cap V$ that is finite and every point in $T\cap V$ is greater than or equal to a point in $S_V$. Then let $S= \left( \bigcup_{V} S_V \right) \cup {(a,b)}$. This is finite as all the sets in the union are finite and there are finitely many of them, and given any point $t\in T$ we either have $(a,b)\leq t$ or $t\in T\cap V$ for some $V$, and then $s \leq t$ for some $s\in S_V$.

For the full inductive proof, if we know the statement is true for $\mathbb{Z}^{n-1}$, then we pick some random $z=(z_1,...,z_n)$ to include in our set $S$. We then select $S_V$ for $V$ any of the $z_1-1 + z_2 - 1 +... + z_n -1$ hyperplanes of the form $x_i=k$ for some $k<z_i$. By induction we can construct these $S_V$ to be a finite subset of $T\cap V$ such that for any $t\in T\cap V$, there exists $s\in S_V$ such that $s\leq t$. Then let $S$ be the union of all the $S_V$ and the original point $z$, and any point in $T$ is greater than either $z$ or is contained in one of the subspaces $V$ where we can find a point in the corresponding $S_V$. By induction each $S_V$ is finite, and there are finitely many of them, so $S$ is finite

 

[bpet]

Yes, but can you show the way?

Which bit would you like me to explain further? Keep in mind I’m tapping this out on a phone here.

Cheers