MATLAB MATLAB Simulation of Fraunhofer Diffraction

[wybmax]

Hello, I am using MATLAB to simulate a Fraunhofer diffraction pattern for a given aperture, but I have a little question. Hope someone can help.

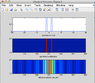
Sorry I am just a high school student and does not completely understand all mathematic deductions about Fraunhofer Diffraction on Wikipedia. I simply learn the way to generate the diffraction pattern: use a matrix of 0 and 1 to describe the aperture, take the Fast Fourier Transform of the matrix, "fftshift" it, display the transformed image to an image, and I get the diffraction.

I made programs for 1-dimensional and 2-dimensional apertures, and the diffraction looks well. But it seems that the diffraction pattern simulated in this way is independent of the frequency (or wavelength) of the incident light. i.e., as long as I get an aperture, I get an only diffraction pattern regardless of the wavelength of the light, because there are no light properties described in my program. In reality that is not the case: for example the wavelength of light determines the distance between two fringes in the double-slit diffraction; for the same double-slit, the shorter the wavelength, the finer the fringes of diffraction pattern.

Well, how can I put wavelength into consideration when I simulate the diffraction?

Thanks.

 

[Orodruin]

The wave length is related to the size of the aperture. For shorter wave lengths, you need a smaller aperture to produce the same result. Thus, since this is numerical, the unit length of your program is likely to be one wavelength of the light (or similar, I have not seen your program). The wavelength is then by definition 1. You could simulate other wavelengths by scaling the aperture.

 

[wybmax]

The wave length is related to the size of the aperture. For shorter wave lengths, you need a smaller aperture to produce the same result. Thus, since this is numerical, the unit length of your program is likely to be one wavelength of the light (or similar, I have not seen your program). The wavelength is then by definition 1. You could simulate other wavelengths by scaling the aperture.

Thanks for your explanation. I will add my 1-dimensional diffraction pattern program and the result for your reference.

And another question: if the wavelength is one unit length in my program, can I simulate an aperture with diameter less than one wavelength? For example, if I want to create a single-slit of 0.5 times wavelength, I cannot split one number in a matrix into two.

Thanks.

-------------MY PROGRAM-----------------
%%% initialize a piecewise function describing the aperture,
%%% then using fft2 to simulate the diffraction pattern.

clear;clc

x=-30:0.1:30; % domain
num=size(x,2);
for i=1:1:num % set initial values for aperture; here is a double-slit
if x(i)<2.5 && x(i)>1.5
y(i)=1;
else
if x(i)<-1.5 && x(i)>-2.5
y(i)=1;
else
y(i)=0;
end
end
end
subplot(3,1,1);
plot(x,y);xlabel('aperture function');
subplot(3,1,2);
imagesc(y);xlabel('aperature for diffraction');

fourier=fft(y); % create diffraction pattern
fourier=fftshift(fourier);
fourier_abs=abs(fourier); % get the intensity of diffraction for display
fourier_abs=mat2gray(fourier_abs);

subplot(3,1,3);
imagesc(fourier_abs);xlabel('diffraction pattern using fft2');

------------------------
The attachment is my screen shot of my program.

 

[olivermsun]

As you show in your subplot(3,1,1), your aperture y(x) is a function of x. However, in your subplot(3,1,3), you're just plotting the Fourier coefficients without specifying any units for your horizontal axis.

When you Fourier transform, you get a function of "something else" which in this case is k sin θ, where the wavenumber k = 2π/λ for wavelength λ and θ is the angle with respect to the axis. (For angles close to the axis, or small θ, you can approximate k sin θ ≈ kθ.)

If you go back and plot the Fourier transform with respect to the proper horizontal units, then the dependence on k (or λ) will reappear. By the way, what this will tells you is that the diffraction pattern never changes shape — it just scales with the wavenumber (inversely with the wavelength) of the incident light.

 

[wybmax]

If you go back and plot the Fourier transform with respect to the proper horizontal units, then the dependence on k (or λ) will reappear.

I generally got what you means. Could you please explain more about how to plot the FT respect to proper units in my program? Thanks.

 

[olivermsun]

Well, suppose you take have a set of N inputs y(x₁), y(x₂), …, y(x_N) at a set of points x₁, …, x_N. The spacing between the x_n's is f_s. This part is easy— you know how to plot y vs. x.

Now you do an FFT on y₁, …, y_N and get a set of N outputs, Y₁, …, Y_N.

The Y_n correspond to a set of (spatial) frequencies k₁, …, k_N, with spacing dk. Do you know how to find dk and get the set of frequencies?

 

[wybmax]

Well, suppose you take have a set of N inputs y(x₁), y(x₂), …, y(x_N) at a set of points x₁, …, x_N. The spacing between the x_n's is f_s. This part is easy— you know how to plot y vs. x.

Now you do an FFT on y₁, …, y_N and get a set of N outputs, Y₁, …, Y_N.

The Y_n correspond to a set of (spatial) frequencies k₁, …, k_N, with spacing dk. Do you know how to find dk and get the set of frequencies?

As this program is a numerical simulation without any physical units, I think we can just assume the spacing (dk) to be 1 unit. I can also change it according to different sampling rate of the object. In this case the wavelength may also be a number related to the 'unit' defined above, not to our normal unit like 'nanometer'.

Also, I have to know the angle θ to calculate the independent variable of Fourier transformed function. Do I have to get the distance between the object and the screen? Or is there a way of approximation in Fraunhofer diffraction?

Thanks.

 

[olivermsun]

As formulated, your 'x' units are indeed in "wavelengths" (times some constant).

The angle is independent of the distance between object and screen, but of course the size of the pattern on the screen will get bigger as the distance gets bigger.