guyvsdcsniper
- 264
- 37
- Homework Statement
- Find the electrostatic force 𝐹⃗ on p.c. q placed inside a large parallel plate capacitor in vacuum, with grounded plates, separated at distance h. The p.c. is at a distance h/4 from the closest plate
- Relevant Equations
- F=kq^2/r^2
Disclaimer: This is not a repost.
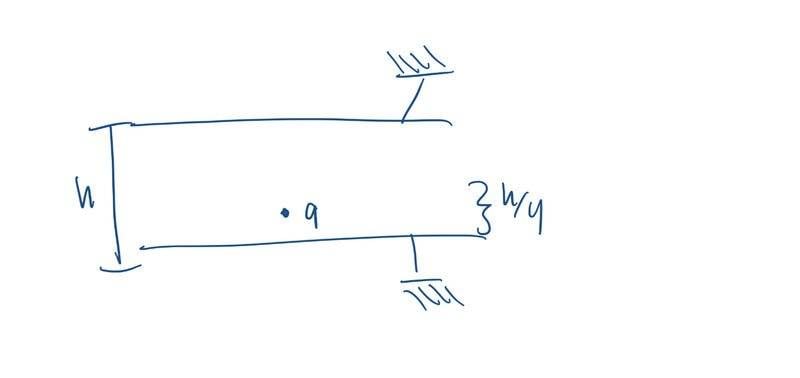
The problem wants me to calculate the force of a p.c. , that is isolated by itself (this p.c. is the only charge this problem starts with in this problem) inside a capacitor, a distance h/4 from the bottom plate.
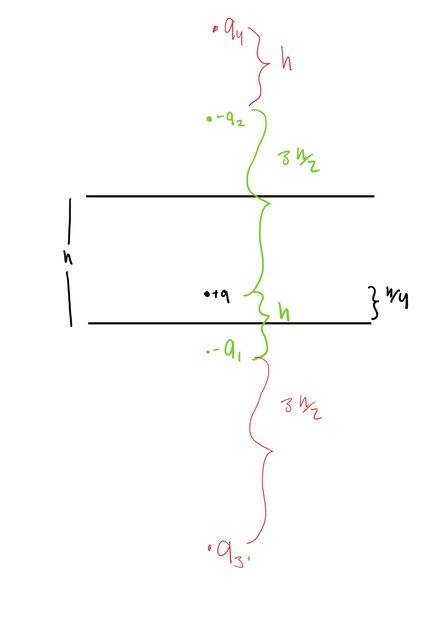
This is what I have though of so far but I don't think this really satisfies the method of images since after my second iteration (red charges) +q is still "free".
I recall a substitute professor once showing me an example like this, and from my notes he said this problem would look like this
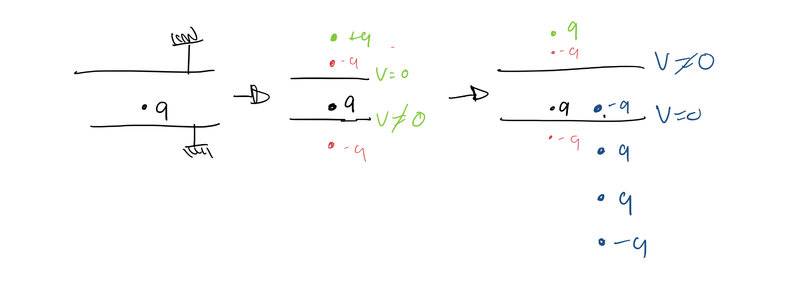
Where this seems like it would go on forever but I THINK he said you would get an answer around the 10th iteration. I honestly don't remember that well since it was a while back.
Could I get some help with this problem
The problem wants me to calculate the force of a p.c. , that is isolated by itself (this p.c. is the only charge this problem starts with in this problem) inside a capacitor, a distance h/4 from the bottom plate.
This is what I have though of so far but I don't think this really satisfies the method of images since after my second iteration (red charges) +q is still "free".
I recall a substitute professor once showing me an example like this, and from my notes he said this problem would look like this
Where this seems like it would go on forever but I THINK he said you would get an answer around the 10th iteration. I honestly don't remember that well since it was a while back.
Could I get some help with this problem