Need help understanding the twins

[yuiop]

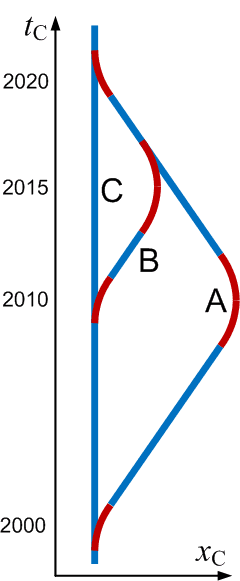
The issue of whether the differences of time dilation in the twins paradox is caused by acceleration or relative velocity has come up several times in this thread. The diagram below (created by Dr Greg a long time ago) shows a way to eliminate acceleration from the considerations. Observers A and B undergo identical acceleration events (The curved sections highlighted in red) and yet less proper time elapses for observer A than for observer B. The difference in time dilation in this example can only be accounted for by the difference in time spent at higher relative velocities.

 

[ExecNight]

---------------- Twin A and Twin B ---------------- ;

Twin A ----------------- and ----------------- Twin B;

Here which twin moved which way? While an observer might suggest that it was the twin B that moved away from twin A, another observer might suggest it was Twin A that moved away.

Which observer is correct in this situation and which twin will age less when they are back at the same point again. While all objects are considered moving there is no reference point anyone can agree on.

Which leads to the conclusion that the twin that spent more Energy in the process ages less. That is the only universal truth everybody in this experiment will agree on.

So one can associate time dilation with velocity, acceleration etc. But the only relevant conclusion i can make out of this example is that it is simply associated with how much energy is used to create the new reference frame to reach those velocities etc.

Extremely heated particles or super heated material might show small time dilation or length contradiction properties maybe in atomic or subatomic magnitude. One should check it out i guess :P

 

[DrGreg]

Here which twin moved which way? While an observer might suggest that it was the twin B that moved away from twin A, another observer might suggest it was Twin A that moved away.

Which observer is correct in this situation

They are both correct.

and which twin will age less when they are back at the same point again.

That depends on how they get back together again.

------------------- A B ------------------ ;
-----------A ------------------ B--------- ; A and B both turn round
------------------- A B ------------------ ;
Both the same age.

------------------- A B --------------------;
-----------A ------------------ B ----------; A turns round
--------------------------------------- A B ;
B older than A.

------------------- A B ------------------ ;
-----------A ------------------ B----------; B turns round
A B -------------------------------------- ;
A older than B.

"Turning round" can be detected by G-forces and measured by an accelerometer.

 

[JesseM]

Yes.
The twin that will age more slowly is the one that changes inertial frames of reference.

It isn't the acceleration that causes the time dilation, it is the time spent in the traveling frame of reference. Those frames of refrence are high speed frames relative to the twin that is stationary.

Because the traveling twin is returning to the stationary twin's frame of refrence, then the stationary twin's frame of refrence is the clock that you have to go by, because ultimately they both end in that frame of refrence.

Well, it isn't actually necessary that the traveling twin come to rest in the stationary twin's frame. The traveling twin could simply fly by the stationary twin on the inbound leg and they could compare clocks at the moment they passed right next to each other. The only change in velocities that's really important to the problem is the one that happened midway through the traveling twin's trip, between the moment he departed from the stationary twin and the moment he reunited with the stationary twin. As long as you analyze the entire problem from a single inertial reference frame (it doesn't need to be the stationary twin's rest frame, as the right-hand diagram I posted shows), you'll see that the "stationary" twin was traveling at constant velocity between these two events, while the traveling twin changed velocities somewhere between them, so the stationary twin will be the older one (because his worldline is a 'straight line' through spacetime, and in relativity straight line paths are the ones that maximize the proper time).

This might be a confusing example, but it's one that shows an odd view that still works out correctly.

If both twins are traveling past their home planet at high speed, and one twin decelerates to stop and visit their mom. Then accelerates to catch up to the twin that continued on their trip. When the one that stopped catches up and decellerates to match speed with the one that continued, they will find that the one who continued has aged more quickly.

Yup, that's right.

The one that continued, traveled in only one frame of refrence. While the twin that stopped spent time in three, two of which were at high speed relative to the traveling twin. Their ages are then compared to the clock that was always with the traveling twin. So it is the traveling twin's frame of refrence that is correct in this case.

It's actually not a matter of one frame of reference being correct--every inertial frame will get the same answer for how much each twin aged when they calculate how slow their clocks were running during each leg of the journey. You might look back on the calculation I did in the post with the diagram, done from the perspective of the frame where the traveling twin was at rest during the outbound leg of the journey (the same frame the right side of the diagram was drawn from)--in this frame although the traveling twin was aging faster than the stationary twin during the outbound leg, the traveling twin had an even greater velocity than the stationary twin during the inbound leg so he was aging slower during this leg, and the inbound leg lasted much longer than the outbound leg in this frame, so ultimately this frame ended up predicting that the traveling twin aged 8 years over the course of the entire journey while the stationary twin aged 10 (the same prediction you get when you analyze from the stationary twin's frame), even though the "stationary" twin was not actually at rest in this frame and the traveling twin was at rest during the outbound leg.

 

[yuiop]

The diagram below is an old recycled diagram that illustrates the point made at the end of JesseM's last post.

Terra remains in the "stay at home" twin's frame (red path). Stella is always in the reference frame of the outgoing leg of the traveling twin's journey (green path). Alf is always in the frame of the return leg of the traveling twin's journey. All 3 observers agree that the traveling twin takes the longer path through spacetime and ages the least. You could of course take the point of view of any inertial observer and the saem would be true.

 

[yuiop]

Which leads to the conclusion that the twin that spent more Energy in the process ages less. That is the only universal truth everybody in this experiment will agree on.

Are you sure about that?

Take this example. A and B are traveling at 0.8c to the right according to observer C.

C -------> A
C -------> B

B turns around and accelerates to a stop in C's frame while A continues.

C --------------------> A
C --------- B

C now says that less time elapses for A even though it was B that expended energy accelerating to a stop.

 

[ExecNight]

Well, let's see;

When B accelerated away from C it used energy, when it accelarated backwards it again used energy in the process. So yes B aged less than A and C at that exact moment.

If they all unite again at C, B will accelarate again towards C and stop again. Aging even lesser. A will accelerate back to C directly.

In the end C will be a dead man, A is too old to walk and B is fit as a tiger.. I like B.
I think what i am suggesting can be tested. That would be too bad :( I don't like to be proven right.

On a side note i am really curious about the equipment they would choose to use to go on a straight line(for themselves) with the speed 0.8c, and miraclously be able to use the same path backwards :) Considering you don't know the vectoral movement of the rest point in the universe and Space-time curvetures throughout it. I bet if you reached those speeds with the current knowledge, you would have no idea where you would end up :)

Its even more exciting to think about the velocity problem. How do you choose to calculate it? And how B will accelerate backwards, how does he know how much he should accelerate to be able to come to rest relative to C, and well which vectoral movement will he choose?

By the way who is C? We were talking about twins :(

 

[Malorie]

Execnight,
Check the diagram in Kev's first post on this page.

Paths A and B are using the same energy to make their journeys, yet A ages more slowly due to the longer time spent at the travel velocity.

I think you're missing the fact that you can coast indefinately and not use any additional energy.

So I think your suggestion that it comes down to who uses more energy is the younger twin is incorrect.

I also think that your interpritation of Kev's last post is incorrect for the same reason. If they all united again at C, B would be older than A and C would still be dead. Xp

A would be traveling in the high relative velocity frames for a longer period and therefore would age less. A and B would use precicely the same energy for their trips.

 

[ExecNight]

No, i think i understood the diagram and the last example.

Anyway, it is flawed because it doesn't add in the reality that no one knows where they are and where they should accelerate.

C----->B----->A

So in the end with the current universal momentum of C, after the acceleration process B and A might end up like this;


B---A-----C

It is funny how they end up like this, considering they were accelerating the opposite direction. Then you would suggest to me that B traveled more than A and C, but it is quite unclear who spent more time at a different velocity. Because you didn't know about that small space-time tide which distorted your rest momentum with C, and well you are no longer connected in a manner you choose to understand.

Anyway if you could catch my drift, B will end up like that even further away from A because B used more energy in the process ;) B will also age much less.

 

[pervect]

It turns out that when you are in flat space time, you do minimize energy. What happens is that you minimize the Lagrangian, L, which is the kinetic energy minus the potential energy. When the potential energy is zero, the path you take is the one of minimum energy.

In more general cases, though, this approach won't give the right answer.

see for instance http://www.eftaylor.com/leastaction.html#forcingenergy which has a link to a pdf downloadable paper

"Action: Forcing Energy to Predict Motion," Dwight E. Neuenschwander, Edwin F. Taylor, and Slavomir Tuleja, The Physics Teacher, Vol. 44, March 2006, pages 146-152. Scalar energy is employed to predict motion instead of the vector Newton's law of motion.

The idea to minimize energy is evaluated and rejected specifically.

 

[ExecNight]

Reminded me of ZZ Top, good old times.

That was poetic, but in the end i am simply going to say what is the Lagrangian of the system we are talking about?Yes well, in my imaginary space craft, i used some of the potential energy i had at my disposal for the acceleration process. So i would say i am turning pedals uphill now, while you are still going downhill. That doesn't necessarily mean i am moving away from you. Actually while i am accelerating you are the one that is moving away from me. I simply have changed my potential and kinetic energy in space-time :P But its ironic that i don't know any reference point's potential energy to start with to know what exactly this change was..

Something is really wrong but what? hmm..

 

[Buckethead]

To eliminate the effect caused by acceleration and to identify that effect caused only by velocity the following scenario can be proposed:

Two explorers start from the Earth and accelerate off in the same direction and at the same rate. When they reach .9999c explorer A decelerates at the same rate that she accelerated at and when she comes to a stop, turns around and accelerates/decelerates back to Earth again at the same rate of acceleration.

Explorer B however after reaching .9999c cuts his engine and coasts at this speed for a year. At the end of the year, he too decelerates, turns around accelerates, coasts for a year, then decelerates to the final Earth destination to meet up with A.

Both astronauts have accelerated at the same rate for the same length of time and in the same directions. The only difference between the two is that astronaut B spent two years at a constant speed of .9999c.

Their age difference can now be attributed strictly by one's lenth of time at near light speed with respect to the other without acceleration being part of the equation.

 

[Buckethead]

My crackpot meter is going off scale high.

Wow! this was uncalled for. Malory is right, if a laser is projected there is no way to determine if it is going in a straight line unless a straight line is defined as "what is made if a laser beem is projected" and last I checked this was not the official definition of a straight line. Please try to consider what a person is saying before dismissing it so easily with an insult and better still try refraining from insults altogether.

 

[cfrogue]

To eliminate the effect caused by acceleration and to identify that effect caused only by velocity the following scenario can be proposed:

Two explorers start from the Earth and accelerate off in the same direction and at the same rate. When they reach .9999c explorer A decelerates at the same rate that she accelerated at and when she comes to a stop, turns around and accelerates/decelerates back to Earth again at the same rate of acceleration.

Explorer B however after reaching .9999c cuts his engine and coasts at this speed for a year. At the end of the year, he too decelerates, turns around accelerates, coasts for a year, then decelerates to the final Earth destination to meet up with A.

Both astronauts have accelerated at the same rate for the same length of time and in the same directions. The only difference between the two is that astronaut B spent two years at a constant speed of .9999c.

Their age difference can now be attributed strictly by one's lenth of time at near light speed with respect to the other without acceleration being part of the equation.

I have a simpler twins experiment

O, O', twin1 and twin2 are in the same frame and sync their clocks.

O and twin1 accelerate for some agreed upon time BT at a.

Then for a long period of time there exists relative velocity.

Finally, O' and twin2 perform the same acceleration for BT as twin1 and in the same exact direction.

The accelerations are symmetric and so they end up in the same frame again but at a distance.

They all perform Einstein's clock synchronization method to test the time differences of the clocks.

What will O conclude about the age ordinality of the twins?

What will O' conclude about the age ordinality of the twins?

 

[ExecNight]

Ok, here is my experiment then :)

Twins, A and B they set their clocks and use Swatch synchronization.

Now Twin B will not move and Twin A will fly past with his spaceship 10 kms away from Twin B(from B's POV),

Twin A uses the calculations(which are actually wrong) and flies as agreed.

Twin B on the other hand innocently watch Twin A as Twin A flies by the agreed coordinates. But then something happens and from Twin B's POV Twin A's spaceshift's energy level is so high that the spaceshift just dissappears from sight leaving behind a deadly gravitational wave, which distorts space-time on that frame for any object relatively traveling at or below c.

Because for Twin B, Twin A's pass just killed him as Twin A reached the required relative speed sucking him into a singularity. After a while Twin A returns back as agreed. Also getting sucked into the singularity. Then i go and find their watches and realize that they are fake swatches.


So maybe this time when they are out of the singularity, they will try making a valid experiment accepting the fact that they can't find each other again after reaching a certain relativistic speed :)

Hello cfrogue,

Two real objects can not be in the same coordinates so they will experience different paths. Ending up in different places using same calculations.

One of the twins will age less(the differnece increasing in direct proportion to their rest distance). Which twin will age less can not be calculated with the variables at hand.

 

[cfrogue]

Ok, here is my experiment then :)

Twins, A and B they set their clocks and use Swatch synchronization.

Now Twin B will not move and Twin A will fly past with his spaceship 10 kms away from Twin B(from B's POV),

Twin A uses the calculations(which are actually wrong) and flies as agreed.

Twin B on the other hand innocently watch Twin A as Twin A flies by the agreed coordinates. But then something happens and from Twin B's POV Twin A's spaceshift's energy level is so high that the spaceshift just dissappears from sight leaving behind a deadly gravitational wave, which distorts space-time on that frame for any object relatively traveling at or below c.

Because for Twin B, Twin A's pass just killed him as Twin A reached the required relative speed sucking him into a singularity. After a while Twin A returns back as agreed. Also getting sucked into the singularity. Then i go and find their watches and realize that they are fake swatches.


So maybe this time when they are out of the singularity, they will try making a valid experiment accepting the fact that they can't find each other again after reaching a certain relativistic speed :)

Hello cfrogue,

Two real objects can not be in the same coordinates so they will experience different paths. Ending up in different places using same calculations.

One of the twins will age less(the differnece increasing in direct proportion to their rest distance). Which twin will age less can not be calculated with the variables at hand.

what if I said humor is always good and this was funny.

 

[pervect]

Oh - it was a joke? He actually got the part about a gravitational wave right - though I doubt it would kill anyone, unless one of the twins was REALLY heavy. The rest was a bit muddled, but not that much more muddled than a lot of posts I see on here that are (supposedly, at least) serious :-) :-(.

 

[ExecNight]

Its not the twin that is heavy, he don't like Burger King! Its his spaceship..

Well the spaceship is quite heavy, around 4.2 SunMass. Actually it is not the spaceship that is heavy. It just contains one reactor to keep the charged singularity let's say under control. How did you think he could accelerate up to c speeds, by swiming in empty space? :P

 

[cfrogue]

post #49 Jesse.

 

[JesseM]

I have a simpler twins experiment

O, O', twin1 and twin2 are in the same frame and sync their clocks.

O and twin1 accelerate for some agreed upon time BT at a.

Then for a long period of time there exists relative velocity.

Finally, O' and twin2 perform the same acceleration for BT as twin1 and in the same exact direction.

The accelerations are symmetric and so they end up in the same frame again but at a distance.

They all perform Einstein's clock synchronization method to test the time differences of the clocks.

What will O conclude about the age ordinality of the twins?

What will O' conclude about the age ordinality of the twins?

Since O and O' end up in the same frame, why do you ask what they'll conclude separately? Presumably you mean "what will they conclude about the ages of the twins in their own rest frame", and since they share the same rest frame, naturally they'll conclude exactly the same thing about the twin's ages. Anyway, the answer in this frame will be that the twin who accelerated second will be younger than the twin who accelerated first.

 

[cfrogue]

Since O and O' end up in the same frame, why do you ask what they'll conclude separately? Presumably you mean "what will they conclude about the ages of the twins in their own rest frame", and since they share the same rest frame, naturally they'll conclude exactly the same thing about the twin's ages. Anyway, the answer in this frame will be that the twin who accelerated second will be younger than the twin who accelerated first.

Here is the math.

Calculations of O for the twins

Elapsed proper time calculation for twin 1
twin1's acceleration phase
BT
twin1's relative motion phase
t'
twin2's acceleration phase
ta'
But, as shown above in the links, BT = c/a asinh(ata'/c).
aBT/c = asinh(ata'/c)
sinh(aBT/c) = ata'/c
c/a sinh(aBT/c) = ta'
Please note this derivation will be used throughout the below also.
Total elapsed proper time calculation of O for twin1 BT + t' + ta' = BT + t' + c/a sinh(aBT/c)

Elapsed proper time calculation for twin 2

twin1's acceleration phase
c/a sinh(aBT/c)
twin2's relative motion phase
t'/ λ
twin2's acceleration phase
c/a asinh(ata'/c) = BT

Total elapsed proper time calculation of O for twin2 c/a sinh(aBT/c) + t'/λ + BT
Conclusion of O, twin1 is older.

Calculations of O' for the twins

Elapsed proper time calculation for twin 1
twin1's acceleration phase
BT
twin1's relative motion phase
t/λ
twin2's acceleration phase
c/a sinh(aBT/c)

Total elapsed proper time calculation of O' for twin1 BT + t/λ + c/a sinh(aBT/c)

Elapsed proper time calculation for twin 2
twin1's acceleration phase
c/a sinh(aBT/c)
twin2's relative motion phase
t
twin2's acceleration phase
BT

Total elapsed proper time calculation of O' for twin2 c/a sinh(aBT/c) + t + BT
Conclusion of O', twin1 is younger.

Since all are now in the same frame, they again use Einstein's clock synchronization method for the actual hard data of the experiment to test the clocks of the twins for age ordinality. This answer of the clock sync is to be accepted by all those in the frame because as Einstein said, "We assume that this definition of synchronism is free from contradictions". This clock sync can also establish the time ordinality of the clocks.

SR is supposed to be a reliable tool for the calculation of the proper time of one frame to another frame.

However, both O' and O cannot be correct with their SR conclusions when presented with the factual data of the clock sync.*

 

[matheinste]

------Since all are now in the same frame, they again use Einstein's clock synchronization method for the actual hard data of the experiment to test the clocks of the twins for age ordinality. This answer of the clock sync is to be accepted by all those in the frame because as Einstein said, "We assume that this definition of synchronism is free from contradictions". This clock sync can also establish the time ordinality of the clocks. -------

SR is supposed to be a reliable tool for the calculation of the proper time of one frame to another frame.



However, both O' and O cannot be correct with their SR conclusions when presented with the factual data of the clock sync.* ------

You cannot be seriouis. Entertaining though.


As they both end up in the same frame their clocks will be in synch. They will of course not show the same elapsed time. And of course both will agree on these elapsed times. But I suspect you know this

Matheinste.

 

[cfrogue]

------Since all are now in the same frame, they again use Einstein's clock synchronization method for the actual hard data of the experiment to test the clocks of the twins for age ordinality. This answer of the clock sync is to be accepted by all those in the frame because as Einstein said, "We assume that this definition of synchronism is free from contradictions". This clock sync can also establish the time ordinality of the clocks. -------

SR is supposed to be a reliable tool for the calculation of the proper time of one frame to another frame.



However, both O' and O cannot be correct with their SR conclusions when presented with the factual data of the clock sync.* ------

You cannot be seriouis. Entertaining though.


As they both end up in the same frame their clocks will be in synch. They will of course not show the same elapsed time. And of course both will agree on these elapsed times. But I suspect you know this

Matheinste.

the math is above.

let me know

 

[cfrogue]

------Since all are now in the same frame, they again use Einstein's clock synchronization method for the actual hard data of the experiment to test the clocks of the twins for age ordinality. This answer of the clock sync is to be accepted by all those in the frame because as Einstein said, "We assume that this definition of synchronism is free from contradictions". This clock sync can also establish the time ordinality of the clocks. -------

SR is supposed to be a reliable tool for the calculation of the proper time of one frame to another frame.



However, both O' and O cannot be correct with their SR conclusions when presented with the factual data of the clock sync.* ------

You cannot be seriouis. Entertaining though.


As they both end up in the same frame their clocks will be in synch. They will of course not show the same elapsed time. And of course both will agree on these elapsed times. But I suspect you know this

Matheinste.

Yes, but I avoid this correct answer.

It enrages the natives.

 

[JesseM]

Here is the math.

Calculations of O for the twins

Elapsed proper time calculation for twin 1
twin1's acceleration phase
BT
twin1's relative motion phase
t'
twin2's acceleration phase
ta'
But, as shown above in the links, BT = c/a asinh(ata'/c).

That last equation doesn't make any sense, you said in the original problem that twin2 accelerates in an identical manner to twin1, so if twin1 accelerates for time BT then so should twin2. Also, are these times stated in the frame where the twins were originally at rest at the start? If so, in the rest of your calculations you don't even consider the new definition of simultaneity in the rest frame of O and O' after the acceleration, showing that you've missed the point entirely.

Anyway, the problem is easiest to consider if they both accelerate instantaneously. Suppose they are initially at rest in frame #1, both at position x=0 in this frame. Then at t=0, when both twins are aged 20, twin1 instantaneously accelerates to 0.6c, and continues at that velocity. After 10 years, twin2 accelerates to 0.6c in an identical manner.

So, twin1 accelerated at x=0,t=0 (age 20), and twin2 accelerated at x=0,t=10 (age 30). So, let's apply the Lorentz transformation to find when these acceleration events occurred in frame #2 which is moving at 0.6c relative to frame #1, where both twins come to rest after acceleration. The Lorentz transformation is:

x' = gamma*(x - vt)
t' = gamma*(t - vx/c^2) (and we can ignore the c if we use units where c=1, like light years and years).
gamma = 1/(1 - v^2/c^2)

So with v=0.6c, we have gamma=1.25. If we plug in x=0 and t=0 into the above transformation, we get back x'=0 and t'=0. If we plug in x=0 and t=10 into the above, we get:

x' = 1.25*(0 - 0.6*10) = -7.5
t' = 1.25*(10 - 0.6*0) = 12.5

So, in this frame--the frame where O and O' will be at rest after both twins have accelerated--twin 1 accelerated at x'=0, t'=0, after which twin 1 was at rest and twin 2 was moving at 0.6c, then twin 2 accelerated at x'=-7.5, t'=12.5, after which twin 2 was at rest. During the 12.5 years between twin 1 accelerating and twin 2 accelerating, twin 1 was at rest so he aged 12.5 years, while twin 2 was moving at 0.6c so he only aged 12.5*sqrt(1 - 0.6^2) = 12.5*0.8 = 10 years, so he was 2.5 years younger than twin 1 at the moment he accelerated. Then after twin 2 accelerated too, twin 2 was at rest as well, so they both aged at the same rate after that. Thus at all times after twin 2 accelerates, twin 2 is 2.5 years younger than twin 1 in this frame.

 

[cfrogue]

That last equation doesn't make any sense, you said in the original problem that twin2 accelerates in an identical manner to twin1, so if twin1 accelerates for time BT then so should twin2. Also, are these times stated in the frame where the twins were originally at rest at the start? If so, in the rest of your calculations you don't even consider the new definition of simultaneity in the rest frame of O and O' after the acceleration, showing that you've missed the point entirely.

I said they accelerate the same way.

Where do you bring in R of S?

 

[matheinste]

the math is above.

let me know

How would you like to talk us through the mathematics, step by step, explaining each step and then there can be no misunderstandings.

Matheinste.

 

[cfrogue]

How would you like to talk us through the mathematics, step by step, explaining each step and then there can be no misunderstandings.

Matheinste.

Sure, let me deal with Jesse's R of S first.

 

[JesseM]

I said they accelerate the same way.

So doesn't that mean they accelerate for the same amount of time?

Where do you bring in R of S?

We want to know who will be older according to the definition of simultaneity in the final rest frame of O and O', do we not?

 

[Jorrie]

I have a simpler twins experiment

O, O', twin1 and twin2 are in the same frame and sync their clocks.

O and twin1 accelerate for some agreed upon time BT at a.

Then for a long period of time there exists relative velocity.

Finally, O' and twin2 perform the same acceleration for BT as twin1 and in the same exact direction.

I'm contemplating converting your scenario to a non-accelerated, three inertial frame situation for discussion, but first I must understand your scenario.

Your definition of frames O and O' is a bit confusing. At the beginning and at the end, O and O' are the same frames, whereas for the 'middle part', before Twin2 has completed acceleration, they are not the same.

I think you must define O' as the original inertial frame, with both twins at rest and O as the final inertial frame, where both twins are at rest again. You can obviously have a Twin1 frame and a Twin2 frame as well, but they are not inertial and hence not the same as O and O'. I suspect that the math that you posted later may be influenced by such frame definitions.

 

[Fredrik]

I can only interpret #49 as saying that the two twins start out at rest at the same location in some inertial frame. Then A accelerates with constant proper acceleration a for a proper time t, and then he stops. Some time later B does the exact same thing.

If that's what cfrogue meant, what happens is that when B has stopped, he's at the exact same location as A and has aged exactly the same. This follows immediately from the definition of proper time and the fact that you can obtain B's world line by adding the same constant vector to every point on A's world line.

 

[Jorrie]

If that's what cfrogue meant, what happens is that when B has stopped, he's at the exact same location as A and has aged exactly the same. This follows immediately from the definition of proper time and the fact that you can obtain B's world line by adding the same constant vector to every point on A's world line.

No, I think he meant that A stopped accelerating, not stopped in motion relative to B. A and B will eventually be a long distance away from each other, but in the same (new) inertial frame again.

 

[Fredrik]

OK, in that case, at any time in the original rest frame, the one who started accelerating first is younger. They'll be a distance v/t apart, where t is the time between the moments when they started accelerating, and v is their final velocities (which are both the same). The age difference will be $t-t/\gamma$.

 

[JesseM]

OK, in that case, at any time in the original rest frame, the one who started accelerating first is younger.

I didn't think he wanted the answer in the original rest frame, but rather in the new rest frame of O and O' who have traveled along with the twins. In this case the twin who accelerated second will be younger.

 

[ExecNight]

O and twin1 accelerate for some agreed upon time BT at a.

Then for a long period of time there exists relative velocity.

Finally, O' and twin2 perform the same acceleration for BT as twin1 and in the same exact direction.

The accelerations are symmetric and so they end up in the same frame again but at a distance.

I don't know how i can be more clear when saying that, they CAN NOT make a symmetric acceleration starting from different t coordinates in a circular motion based, three dimensional universe.

So even if they sign every treaty to do the same things. They will end up in different frames.

If i accept the assumption that they accelerate symetrically and reach the same frame, still which twin will be younger can not be calculated because the energy used in the acceleration process is an unknown for the other twin. The reason being explained in the first paragraph and the twin that used more energy in the process ages less.

;)