Newbie needed torque/moment arm design assistance

[Skyman]

Folks, hopefully someone can assist me. I am a EE by education and am in the process of designing a mechanism that I need some assistance on.

The basic issue I face is determining the torque needed for a miniature drive motor/gearbox for this mechanism. The problem, I think, might be fairly complex and to be honest I am not sure where to start. The small motors I need to use (22 to 26mm diameter) are a constraint of the design and mechanism size.

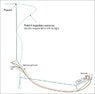
The basic problem involves a motor driven "shuttle" that traverses a curved profile guide rail system over a length of about 12.5". Attached to the shuttle is an arm of about the same length with about a 1lb mass at the opposite end to where this drive motor will be mounted - the shuttle (motor/shuttle is mounted at the base of the arm).

When the shuttle is at one end of the guide rail profile, the arm rests in a vertical position with respect to the shuttle (directly above it) while at the other end of the guide rail profile the arm rests in a near horizontal position and the shuttle is located 12.5" behind the "top" of the arm. The shuttle needs to traverse the curved rail profile over a period of 5 to 6 seconds and have sufficient torque to handle the transition of the arm from vertical to horizantal and vise versa.

I have attached a simple drawing of the mechanism and was wondering if anyone could assist me in determining the motor and gearbox (planetary type) torque needed to authoritatively run this mechanism.

Thanks in advance

 

[Danger]

Welcome to PF, Skyman. I don't actually know how to figure this out. Going by your diagram, though, the maximum torque requirement appears to be about 1/2 shuttle-length short of the vertical resting position. It's hard to be sure; it looks as if at that point the shuttle/arm assembly will be angled backwards trying to tip over.

 

[Skyman]

Danger - yes the arm does tip backwards (to the right in the picture) for a short period of the traverse and then back to vertical and the tips the other direction (to the left in the picture) all the way down to the more hoizontal position.

In my mind however, the peak torque to move the shuttle/arm would be required when the arm is in its horizontal position and the shuttle/motor drive mechanism is to the far right in the picture.

This is the arm position where the full weight of the 1lb mass is acting along the 12.5" arm and therefore on the drive motor gear in the shuttle. I believe the effective moment arm is 12.5 inch lbs at this point with respect to the drive gear noted in the picture (right side). When the arm tips backwards from it's vertical position as you note, it does so by about 2". If my memory serves me well from my collage days (28 years ago) the resultant vector of force acting at the shuttle is considerably less at this point than the 12.5inch lbs when the shuttle is all the way over to the right - if my memory serves me correctly!

Of course, my memory may not be serving me well and I could have it all wrong!

If not, it seems to me that it is a question of deriving the rotational torque of the motor drive gear to overcome the load presented at the end of the arm to traverse the shuttle from the far right in the picture to the far left. As the shuttle traverses from the right to the left, my mind also tells me that the required torque to continue the traverse reduces to a minimum up to the point where the arm first becomes vertical (due to the arms rotation), then increases slightly as the arm passes the vertical and starts to tip backwards and then reduces once more and the arm finally rests vertical at the left most position.

Here lies the main question - how do I calculate this. Right now, the motor gear is a 0.7" pitch diameter sprocket (15 tooth) that runs on a chain link rail that parallels the profile curve noted in the picture. The motor and gearbox delivers 2 inch lbs at the output shaft and uses a 1:1 gear ratio to the main drive shaft where the 15 tooth sprockets are.

I am wondering if the torque required to move this arm is simply a case of calculating the equivalent torque at a radius of 0.35" (half the PD of 0.7 of the sprocket) by dividing the 12.5 inch lbs down - but I'm not really sure.

Tony

 

[Danger]

You might well be correct about the maximum torque; I'm really no good at figuring things out from real engineering principles because I've never studied anything like that. My reasoning regarding my idea about the maximum point is that gravity, inertia, and friction are pretty much the only forces that you have to overcome. Since the inertia and friction shouldn't change, the vertical position is the one in which gravity would have the most effect. While there's a horizontal component of movement, won't the rails, rather than just the drive train, be supporting part of the weight?
Regardless, I really don't know what formulae would be involved.

 

[FredGarvin]

It's tough to see how the arm would actually pivot around a motor to allow that kind of motion. It does indeed appear to be a dirty little dynamics problem (albeit 2D).

 

[Danger]

It's tough to see how the arm would actually pivot around a motor to allow that kind of motion.

Hmmm... I'm not having a problem with that. Maybe it's because I'm used to sketching up stuff like that, but I can pretty clearly see the setup as a 3D construction. (At least, I think that I do.)
If I'm reading it correctly, the arm itself doesn't pivot at all. It's solidly attached to the shuttle. So are the motor and drive gear system. It appears to work similarly to a 'donkey engine', but with a chain to follow rather than a rope.
Unfortunately, that doesn't do a damned bit of good toward me figuring out the problem.

 

[AlephZero]

One simple place to start (to get some insight into what's going on, not an "accurate" answer) would be to assume the guide rail pins are frictionless, and calculate the static torque needed to hold the device steady at different points on the track.

Obviously that's leaving out a lot of details, but at would give you an order of magnitude idea how powerful the motor needs to be.

If all else fails, step 2 would be build a prototype with a motor 5 times as powerful as that estimate, and start testing

 

[Skyman]

Fred, Danger is correct. The arm is fixed to the shuttle as is the driver motor and the two sprockets that drive the shuttle over the curved profile. The shuttle is about 70mm wide and there is a sprocket on either side of it in the location shown in the drawing.

At the two locations showing the guide pins are two pins that go all the way through the shuttle and stick out about 15mm either side where shown. The profile itself in the picture is a representation only. On the final assembly, the profile represents two guide "rails" as such, either side of the shuttle - essentially "sandwiching" the shuttle with applicable clearances for the shuttle to move between them.

The guide pins at the lower left front and lower right rear slide in slots in the guide rails and are directed/positioned by these slots in the rails as the shuttle traverses the distance from end to end. The Sprockets engage a length of chain embedded into the guide rails just above the slots for the pins and provide the translational motion of the shuttle from end to end with the guide pins controlling the trajaectoy.

I have added a second picture with some additional positions of the arm/shuttle assembly. You will notice that the two guide pin locations follow the profile curve and that the black circle above each position represented shows the drive sprockets that are attached to and on either side of the shuttle.

I just also saw a reply in my mail as I was typing this from AlephZero regarding static torque. I can calculate the theoretical static torque at many positions along the profile with simple T=FxL and T=Fx(L x cosa). What I really need to understand is the next step. The moment arm and static torque is for the arm. The motor however, translates torque to the rail through a 0.7" PD sprocket. Do I assume that if the transmission of a force through the spockets is made at a radius of 0.35" that the torque required REDUCES a proprotional amount - is this correct theory? If it is I know how to proceed.

 

[Skyman]

AlephZero - ooops! I just reread your e-mail. "Hold it steady" is the key I think and I believe you mean put the shuttle/arm on the rails and attached a spring scale to see what force is needed to hold the unit in certain positions along the curve.

This, to me, implies a prototype of the shuttle with arm and rails. Since the materials for each are exotic (carbons predominantly), I will need to construct a prototype from alternate materials and estimate but this is a good idea - thanks. Just wish I knew how to crunch the numbers to find the starting range I should consider.

Thanks again.

 

[FredGarvin]

Fred, Danger is correct. The arm is fixed to the shuttle as is the driver motor and the two sprockets that drive the shuttle over the curved profile.

That's what wasn't clicking for me. Now it makes sense. I'm slow but I'm...slow. As the sprocket grows in size the force transmitted through it decreases but since the output sprocket is directly on the motor shaft, it will have the same torque as the motor (if I am understanding your question correctly. It's been a long day).

Ideally you would need to calculate the moment of inertia of your rotating hardware and also the angular acceleration you would wish to impart on the arm. This is a pretty tough dynamics problem. You have differing angular accelerations of the shuttle arm and mass plus a varying acceleration in the translation of the whole thing. As a first run I would pick the worst case section on the track and hold the entire assembly rigid at that point in time. At that point calculate the required force to produce a certain linear acceleration and back that to the motor via the sprocket size.

I would really need to look back at my old dynamics notes on relative reference frames, etc...I am seriously rusty in that department.

It's a cool problem to work on though.

 

[Skyman]

FYI, I have added a couple 3D renderings of a very early version of the concept here for those that may need a visualization. The two pictures cover the "up" position and the "down" position and shows the rails either side of the shuttle/arm assembly. Note that the sprocket positions have since changed relative location to more reflect the positions in the 2D drawing.

The 2D drawing shows the motor position with respect to the drive sprocket and the rotational motion of the motor is translated to a bevel gear on the drive shaft for the two sprockets. The new profile curve (orange) is the profile the sprocket follows and is offet from the guide pin slot profile.

Any other help anyone can give - even detail mathematical concepts and ideas would be gladly welcomed. I would really like a base torqu to work with as there are many motors and gearboxes available to choose from and they can be fairly expensive.

Again, thanks in advance

 

[Skyman]

Apologies for over doing this but one more picture that shows the trajectory curve of point A noted at the top of the picture as the shuttle moves from the left most position to the right most position. This is the motion of this point over the whole shuttle movement from arm vertical to arm horizontal.

Again, thanks

 

[Q_Goest]

I’d agree with Fred, that doing a really accurate job on this would be very difficult. Doing something simple such as Aleph and you have suggested is probably sufficient anyway.

Just ‘thinking out loud’ here… I was going to suggest creating your CAD model and show about 10 points between the two extremes of motion – kinda like what you’ve shown in your “Torque Diagram-2.jpg”. You want the motion of the shuttle or arm (not sure what you’re calling it) to traverse the entire length in 5 or 6 seconds. If you assume the motion along the slider is constant velocity, then put those 10 points half a second apart for example.

Take a look at the 10 points now and consider what power is needed to transverse the various points.
- The weight of the shuttle/arm is one issue. It rises some distance per unit time which directly equates to power. (ie: Power = weight * height / delta-time)
- Also, the entire arm has to go through some rotationial acceleration. If you can estimate the moment of inertia of the unit around that point, you can then calculate power needed to for this rotational acceleration.

Not sure how much each might contribute to the overall power needed, but I’d bet the lifting of the weight is the primary contributor. Do that first and maybe add 50% to 100% and you’ll probably be in the ball park. . . . <still thinking>

 

[AlephZero]

The power to lift 1lb through 1ft in 5 seconds isn't much. I make it about 4N x 0.06m/sec = 0.25W. A 2 in-lb torque motor could do it as a straight lift with a 4in diameter drive, so that doesn't seem like the problem.

Looking at the picture in post #8, one thing that could be worrying is the reactions at the pins when the arm is horizontal. In position 6 the 1lb weight is going to give forces of about +5 and -4 pounds on the pins because of the lever effect. Compare with position 2 where you will get about +0.5 pounds on each pin. So the friction force at position 6 is going to be about 9 times what it was at position 2 - i.e. (5+4)/(0.5+0.5).

One way to reduce those forces is a have a longer "wheelbase" on the track, but that might lead to other complications.

Actually I was thinking of calculating the forces to hold the structure steady, but there's nothing wrong with measuring them instead!

 

[Skyman]

AlephZero - thanks for the additional help - I am reading intently!

Your thoughts are somewhat simialr to what I thought regarding position 6 being the problem area. I have spent quite some time trying to figure out a method of reducing the friction forces between the pins and the slots they ride in. The two concepts were lining the slots with a dry lubricant laminate strip which I think would be a construction issue and secondly some form of bearing on the pin. My current concept is a 2 stage bearing on the pin, the first being a needle roller bearing on the pin that would be retained on one end by a secondary small thrust bearing. The slot would then be machined about 0.005" larger than the outer diameter of the needle roller bearing and the needles would roll on the pin and the outer casing would in turn "roll" on one or the other of the slot upper and lower surfaces. The thrust bearing would then be placed between the roller bearing and the shuttle framework and be used as a bearing surface for one end of the roller bearing.

The problem area is the other end of the roller bearing/pin inside the slot which I cannot attach any bearing surface to - it would essentially "rub" against the inner face of the slot potentially causing friction and particle generation leading to increased wear. I guess a dry lub laminate of some slippery material like PTFE could be used here but I'm not sure. This was the best I could come up with to date.

If you have any alternate methods I could consider to reduce the frictional interface. I added a drawing.

Also, if there is any way you could explain your formulas I would really appreciate it. Power for a EE is volts x amps which I think does not work here!

I really appreciate you taking the time to describe this for me.

Thanks

 

[Danger]

Now that I've seen the 3-D version, the purpose is obvious. Sheer genius! I never would have thought to make an electric ice-cream scoop.

Anyhow, as for your 'problem area'... could you use tapered roller bearings to take care of thrust and rolling friction at the same time? That would minimize the end-play.

 

[Skyman]

Hmm, tapered roller bearings - didn't think of these.

The purpose of the thrust bearing on the pin is two fold

1). To provide a true thrust bearing function to control rotation in the XY plane and
2). as a rotating surface for the outer casing of the roller bearing to bear on as it rotates, if it rotates, during the shuttle transit from one end to the other.

From the research I did on the web, I believe that tapered roller bearings would only provide the function of the thrust and/or roller function but the outer casing of the roller bearing would not have a rotating surface to bear on as the shuttle traverses from one end to the other.

Now, if the tapered roller bearing had a tapered outer casing, that would be a different story. In this case, the inner race would lie on the shaft and if the slots in the rails could also be machined with the same taper as the outer casing it would work as I require it to.

In my limited experience with bearings, a tapered bearing could possibly work in combination with a standard thrust bearing as a rotating surface for the roller bearing outer casing and a tapered sleeve over the outer casing to engage in a tapered slot. A picture paints a thousand words!

Now, I see another problem with this design. If there is play in the XY plane, I can see a condition where the top and bottom suface of the tapered sleeve coming into contact with the top and bottom surface of the guide slots therefore stopping rotation of the roller bearing. This would be bad from a frictional perspective but I only thought of this after I sketched it - erhaps there is further development on this idea!

 

[Skyman]

Anyway, going back to the question of friction forces noted by AlephZero, can someone please help me understand the magnitudes of these forces in relation to the torque selection for the motor?

I have multiple motor/gearboxes I can select from as well as output torque capabilities however, the more torque I have inside the mechanism, the higher the cost of the motor/gearbox combination. 2 inch lbs is about the minimum I was considering and I can go up to about 4 in lbs directly from the gearbox with minimal cost increase. Combine this with the drive sprocket only being 0.36" radius provides me with about 11 lbs of force on the drive chain.

Thanks again for your help.

 

[Danger]

From the research I did on the web, I believe that tapered roller bearings would only provide the function of the thrust and/or roller function but the outer casing of the roller bearing would not have a rotating surface to bear on as the shuttle traverses from one end to the other.

You're right. I didn't think it out completely. The only solution that I see right now (after 10 beers) is to build a 'double trolley' for your shuttle. You could have a subframe with idler wheels that go between your tapered bearings and the top of the track.

 

[AlephZero]

Anyway, going back to the question of friction forces noted by AlephZero, can someone please help me understand the magnitudes of these forces in relation to the torque selection for the motor?

In position 6, imagine "flattening out" your device so you have a see-saw pivoting about the left hand pin. You have a weight of 1 lb a long distance away balanced by the force on the right hand pin a short distance away. I estimated the distance ratio as about 4:1 from your picture, so the force applied to the right hand pin by the track will be 4lb downwards to make the see-saw balance.

So, you have a total force downwards of 4 + 1 = 5 lb. To stop the whole structure falling downwards, there must be a force of 5 lb (upwards) applied to the left hand pin by the track.

On the other hand at position 1, the 1 lb mass is in between the two pins, so the forces applied to the pins by the track are both upwards and add up to 1 lb. If the mass was central, there would be 0.5 lb on each pin.

Assuming a simple model of friction (Coulomb's friction law) the (horizontal) friction forces will be proportional to the (vertical) reactions, and all in the same direction (opposing the motion) So the friction at position 1 is proportional to (0.5+0.5) and at position 6 is proportional to (4 + 5).

Re the power, for a ME work = force * distance, so power = work/time = force * (distance/time) = force * velocity. You need to use consistent units - i.e. a mass of 1 Kg under Earth gravity gives a force of 9.8 Newtons. (By strange conincidence, a force of one Newton is approximately equal to the weight of one apple)

Best to use SI units, since in SI there is a clear distinction between mass units (Kg) and force units (N). "Pounds" is used ambiguously for either "pounds mass" with "pounds force".

Hope this helps.

 

[FredGarvin]

In regards to the bearing set up, I would think a properly pre-loaded angular contact bearing would do what you need to do in stead of having two separate bearings.

 

[Q_Goest]

In regards to the bearing set up, I would think a properly pre-loaded angular contact bearing would do what you need to do in stead of having two separate bearings.

Hi Fred, I'd be interested in understanding what you have in mind. It's not quite clear to me.

Hi Skyman, Regarding types of bearings for the track, I'd also suggest looking into McGill brand "Trakrol" bearings. You can look into the various different types of these bearings here:
http://www.mcgill.co.uk/trakrol_sizes.htm

Because the loading is very low however, these are probably overkill. A simply plastic bushing running on a smooth, hardened rail might work just fine, especially if the number of cycles is low.

 

[Skyman]

AlephZero - perfect and understood. Didn't think of "flattening" the shape before calculating loads but it makes perfect sense now - thank you

Fred - angular contact bearing - I do see how this would eliminate the thrust bearing as long as I could get a bearing diameter small enough to fit in the guide rail slots but I don't yet see how this type of bearing would would stop the outer face of the bearing from rubbing on the inside of the guide slot but I will ponder this further.

Q-Geost - good link and about the only item in their range that could potentially do what I need is the V-grooved roller and a re-design of the guide slots to cater for a v-grooved roller. This would imply both a lower and upper guide for the v-groove since the roller would transition from the top to bottom and vise versa during the end-to-end motion of the shuttle. It is also a shame this company's products have such large diameters - way too large for my application but you have provided an alternate direction of thought. I will dabble further to see if this might work. Many thanks.

AlephZero - one more question if you don't mind. I understand the perpendicular loads on the guide slots from your description of the balanced lever. The question I have is how does a load of 4lbs on the right guide pin translate to additional motor torque I would need to overcome this frictional load IF I have bearings on the pins to minimize the friction content of the load? Do I really need to consider imparting a force of 4 to 5lbs on the guide chain through the drive sprocket to overcome these loads or, with bearings attached to the pins, is it some fraction of these loads? How could I calculate this?

Folks - as always, very much appreciate your time and input of ideas.

Tony

 

[FredGarvin]

My thinking is in the fact that a preloaded bearing would then have more control over the lateral displacement, keeping it pretty much at zero. Most angulars would have more than enough thrust rating to handle what you need. The rubbing on the side could be minimized by making the side of the rail only high enough to get over the OD radius on the bearing itself. A sacrificial guard could be put in place in stead. It could be something along the lines of a nylon fence or teflon. The fence would wear and be replaced from time to time.

What kind of speeds would you be looking at again?

 

[AlephZero]

The simplest model of friction (Coulomb) is friction force = the normal force * the a constant (the coefficient of friction).

I originally took "pin" to mean a fixed pin sliding in a track. Friction cofficients are very dependent on materials and surface finish but typical values for sliding would be in the range 0.1 to 0.3. So the total 9lb normal loads might generate 9*0.3 = 2.7lb friction in a bad scenario.

But rolling friction with bearings would be much lower. Maybe a friction coeff of 0.01 or less, so the friction force would be small (say 0.1lb) compared with the lifting the 1lb weight. The force to move the mass will be about 1lb * sin(theta) where theta is the slope of the track. If your device is rotating through about 90 degrees total, the slope could go from +/- 45 degrees which would give a force of about 0.7lb to lift the mass. If the friction is small compared with that, you don't need to worry about it much.

Often the friction force to get something moving from rest is bigger than the force to keep it moving (usually called the static and dynamic friction cofficients).

Even with rollers, you need make sure the device can't twist sideways and "jam up" against the track though. You might want to think about tapered rails and pins, or flanges (as in the picture in post#17), or whatever, so it is self-centering. If might also depend if it is being "pushed" or "pulled" along the track (but it needs to move both ways so you might not have many options there). What you can do depends how you are going to assemble the complete device - e.g. can you slot the the moving part into the tracks from one end, or can you make it in two halves and bolt them together around the tracks, etc...

 

[Danger]

Skyman, how commited are you to this exact rail set-up? I have a thought toward something that might simplify your project. This might be an echo of what Aleph suggested, but I'm not sure exactly what he had in mind.
I'm wondering about turning your design inside-out. Instead of the groove, how about a pair of bogey wheels sandwiching a horizontal guide flange? For centring, you could add horizontal wheels that contact the outer edge. I think that this would maximize support and control while minimizing friction.

 

[FredGarvin]

Skyman, how commited are you to this exact rail set-up? I have a thought toward something that might simplify your project. This might be an echo of what Aleph suggested, but I'm not sure exactly what he had in mind.
I'm wondering about turning your design inside-out. Instead of the groove, how about a pair of bogey wheels sandwiching a horizontal guide flange? For centring, you could add horizontal wheels that contact the outer edge. I think that this would maximize support and control while minimizing friction.

That's pretty much the way most systems do it but not with a curved rail system like this (at least that I have seen). Ideally a guide rail with two bearings similar to these would work pretty well I would think. Again, finding a way to do it on a curved track would be the trick.

http://www.mcmaster.com/catalog/113/gfx/large/71625kp1l.gif
http://www.mcmaster.com/catalog/113/gfx/large/9904kp1l.gif

 

[Danger]

That's the roller set-up that I had in mind, but rather than that fat rail I was thinking of a strip of #16 or so sheet steel that could be bent to the proper contour and then welded or brazed onto support pieces.

edit: I shouldn't have said 'sheet steel' above; I mean the kind of soft strapping that you can get at hardware stores.

 

[Skyman]

Gentlemen, my sincere apologies. I had to go "offline" there for a couple months due to a family illness related item and haven't responded for a while. Fortunately, I can now get back on track with this.

I think I now have a good grasp of the forces involved in moving this shuttle/arm mechanism but I am still struggling with the pin bearings. Fred/Danger, the last posts you made regarding the idler wheels either side of a bearing surface that would replace the track is a good idea as long as you keep the track/guide width small but my main constraint is size. This mechanism is small and therefore the rollers would also need to be very small, probably no bigger than 1/4" in diameter. In my mind, this type of roller system would need to be pivoted to allow for any correction as the shuttle traverses the rail and that would present other problems like the rollers pinching the rail and jamming as the angles change during the traverse.

I still think the single roller bearing over the the pin is the simplest idea for minimizing friction forces between pins and the guide rail but this still doesn't resolve the requirement for lateral positioning. I did a little more research on this and found a very small spring plunger that can be placed in the end of the pin. This creates a single ball lateral control device except that it is a spring plunger rather than a bearing. See attached. Do you know of a supplier that creates a similar component where the ball actually bears on smaller balls within the body that allows the primary ball to rotate as a bearing?

This particular component has a body width of 1/8" and a flange of 3/16" and fits perfectly into the end of each pin. - See the second attachment. Red = thrust bearing, Gold = roller bearing, cyan = spring plunger

Another alternative is to get a slightly larger version of this and place the roller bearing on the outer surface of the "spring plunger" type bearing component. The key is to find a similar product that is a single ball bearing device.

Thanks

Tony

 

[Skyman]

ooops - forgot second attachment.