Carlos Criollo
- 9
- 0
I am would like to solve this differential equation:
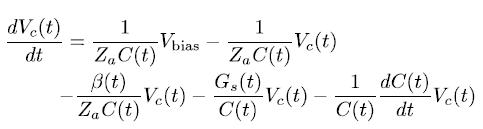
Where
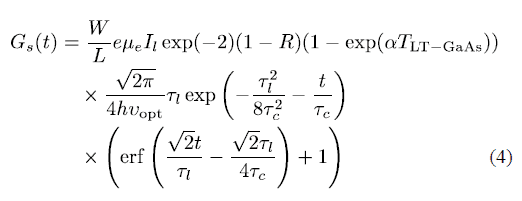
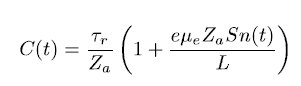
http://ieeexplore.ieee.org.ezproxy.uniandes.edu.co:8080/ielx5/8/6493417/6409989/html/img/6409989-eqdisp-3-small.png
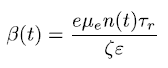
Could you give me some practical ideas about the required software and methodology? Thank you very much
Where
http://ieeexplore.ieee.org.ezproxy.uniandes.edu.co:8080/ielx5/8/6493417/6409989/html/img/6409989-eqdisp-3-small.png
Could you give me some practical ideas about the required software and methodology? Thank you very much