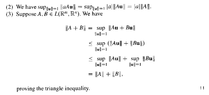Operator norm .... Field, Theorem 9.2.9 ....

[Math Amateur]

I am reading Michael Field's book: "Essential Real Analysis" ... ...

I am currently reading Chapter 9: Differential Calculus in $$\mathbb{R}^m$$ and am specifically focused on Section 9.2.1 Normed Vector Spaces of Linear Maps ...

I need some help in fully understanding Theorem 9.2.9 (3) ... Theorem 9.2.9 (3) reads as follows:
View attachment 9375
View attachment 9376

In the proof of Theorem 9.2.9 (3) Field asserts the following:

$$ \text{sup}_{ \| u \| = 1} ( \| Au \| + \| Bu \| ) \le \text{sup}_{ \| u \| = 1} ( \| Au \| ) +\text{sup}_{ \| u \| = 1} ( \| Bu \| ) $$
Can someone please explain why this is true ... surely the above is a strict equality ...
Help will be much appreciated ...

Peter

 

[GJA]

Hi Peter,

In the proof of Theorem 9.2.9 (3) Field asserts the following:

$$ \text{sup}_{ \| u \| = 1} ( \| Au \| + \| Bu \| ) \le \text{sup}_{ \| u \| = 1} ( \| Au \| ) +\text{sup}_{ \| u \| = 1} ( \| Bu \| ) $$

Can someone please explain why this is true ... surely the above is a strict equality ...

Here is a hint: Use the fact that $\|Au\|\leq \sup_{\|u\|=1}\|Au\|$ and $\|Bu\|\leq \sup_{\|u\|=1}\|Bu\|$ for all $\|u\|=1.$ Can you proceed from here?

 

[Math Amateur]

Hi Peter,
Here is a hint: Use the fact that $\|Au\|\leq \sup_{\|u\|=1}\|Au\|$ and $\|Bu\|\leq \sup_{\|u\|=1}\|Bu\|$ for all $\|u\|=1.$ Can you proceed from here?

Hi GJA ...

I think that a way to proceed is as follows:

Since $\|Au\|\leq \sup_{\|u\|=1}\|Au\|$ and $\|Bu\|\leq \sup_{\|u\|=1}\|Bu\|$ for all $\|u\|=1.$

we have ... ...

$$\|Au\| + \|Bu\| \leq \sup_{\|u\|=1}\|Au\| + \sup_{\|u\|=1} \|Bu\| $$ for all $\|u\|=1.$ Therefore ...$$\sup_{\|u\|=1} ( \|Au\| + \|Bu\| ) \leq \sup_{\|u\|=1} \|Au\| + \sup_{\|u\|=1}\|Bu\|$$... since $$\sup_{\|u\|=1} ( \|Au\| + \|Bu\| ) = \text{ max }_{ \| u \| = 1 } ( \|Au\| + \|Bu\| )$$
Is that correct?Peter