- #1
Oculatus
- 1
- 0
I found this picture somewhere:
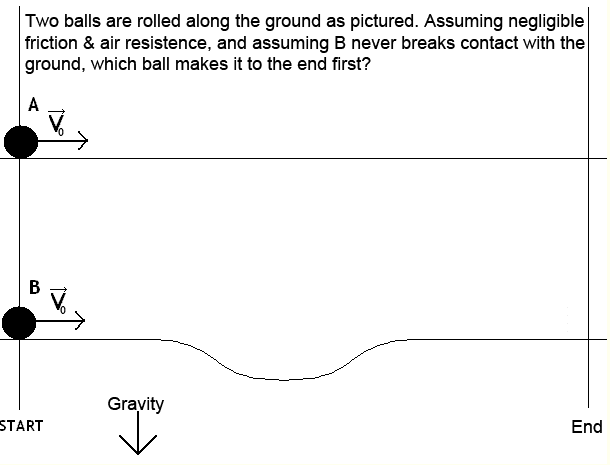
My question being, as in the picture, which ball gets to the end faster? I guess you could naively say that ball A reaches the end in less time, but then again, there is the force of gravity which would accelerate the ball going downwards (and deaccelerate it going upwards, respectively). In essence, the question really might be: does the gravitational pull accelerate the ball to a high enough velocity to compensate for the increased distance? I hope I'm going into the right direction with this, but I certainly lack the mathematical/physical knowledge to solve this (could the conservation of energy be used?).
I'd appreciate any input.
My question being, as in the picture, which ball gets to the end faster? I guess you could naively say that ball A reaches the end in less time, but then again, there is the force of gravity which would accelerate the ball going downwards (and deaccelerate it going upwards, respectively). In essence, the question really might be: does the gravitational pull accelerate the ball to a high enough velocity to compensate for the increased distance? I hope I'm going into the right direction with this, but I certainly lack the mathematical/physical knowledge to solve this (could the conservation of energy be used?).
I'd appreciate any input.