Path of the particle on inclined plane

[Vibhor]

Homework Statement

[/B]

Homework Equations

The Attempt at a Solution

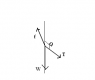
Honestly speaking , I have little idea about this problem . All I can think of is that since the particle is in static equilibrium , the particle has no acceleration .

So , if T is the tension in the string then resolving the forces along the length of the string T = μmgcosθ + mgsinθ . I am not sure if this is correct .

Please help me with the problem .

Thanks

 

[haruspex]

There are two angles to consider: the angle of the plane to horizontal and the angle of the string to a horizontal line that lies in the plane. I believe your equation is confusing the two.

 

[Aditya Bhat]

Here, it is given that tanθ = μ, which means that the inclination, 'θ', is set such that the particle does not slide down. At the same time, the particle is pulled in so slowly that the particle has a constant velocity. So, I guess, the particle moves radially inward.

 

[Vibhor]

There are two angles to consider: the angle of the plane to horizontal and the angle of the string to a horizontal line that lies in the plane. I believe your equation is confusing the two.

I have resolved the forces along the length of the string . I think the angle of the string to a horizontal line that lies in the plane is not required . Or is it ?

 

[Vibhor]

Here, it is given that tanθ = μ, which means that the inclination, 'θ', is set such that the particle does not slide down. At the same time, the particle is pulled in so slowly that the particle has a constant velocity. So, I guess, the particle moves radially inward.

Good point !

I like your reasoning but this does not match the answer given .

 

[haruspex]

Here, it is given that tanθ = μ, which means that the inclination, 'θ', is set such that the particle does not slide down. At the same time, the particle is pulled in so slowly that the particle has a constant velocity. So, I guess, the particle moves radially inward.

No, that does not work. The friction just manages to oppose motion as long as the tendency to motion is directly down the slope and not assisted by the string. As soon as you supply a sideways force, the total force will exceed friction, but the friction now acts to oppose the resultant of the tension and the downslope component of gravity. So the upslope component of friction is no longer sufficient to balance the downslope component of gravity.

 

[haruspex]

I have resolved the forces along the length of the string .

Your equation only fits that statement if the string is directly up the slope from mass to hole.
Try this as a first step. Suppose the string is horizontal from mass to hole. With no tension, you have the friction acting up the slope exactly matching the component of friction down the slope. If you pull very gently on the string, the particle accelerates. Suppose it accelerates at an angle φ to the "downslope" line. Which way is friction now acting? What equation can you write for the acceleration?
Maybe use x for the horizontal direction within the plane and y for the upslope direction.

 

[Vibhor]

What equation can you write for the acceleration?
Maybe use x for the horizontal direction within the plane and y for the upslope direction.

Along x-direction , $Tsin \phi = \mu mgcos \theta sin \phi$

Along y-direction , $Tcos \phi = \mu mgcos \theta cos \phi + mgsin \theta$

 

[haruspex]

Along x-direction , $Tsin \phi = \mu mgcos \theta sin \phi$

Along y-direction , $Tcos \phi = \mu mgcos \theta cos \phi + mgsin \theta$

No, T is acting in the x direction. And don't forget we are at this point assuming some small acceleration. It is premature to neglect that.

 

[Vibhor]

Ok

Along x -direction , $T - \mu mgcos \theta sin \phi = ma_x$

Along y-direction , $-\mu mgcos \theta cos \phi -mgsin \theta = ma_y$

 

[Vibhor]

Which way is friction now acting?

I think initially friction acts opposite to the direction of acceleration i.e at an angle $\phi$ with the y-direction .

 

[haruspex]

Ok

I think initially friction acts opposite to the direction of acceleration i.e at an angle $\phi$ with the y-direction .

Along x -direction , $T - \mu mgcos \theta sin \phi = ma_x$

Along y-direction , $-\mu mgcos \theta cos \phi -mgsin \theta = ma_y$

Right. But there is also a relationship between a_x, a_y and φ.

Edit, no sorry, your second equation is wrong. T is only small. Friction will principally act up the plane still.

 

[Vibhor]

Right. But there is also a relationship between a_x, a_y and φ.

$a_x = asin \phi$

$a_y = acos \phi$

Friction will principally act up the plane still.

Why ?

This is what you objected to in post#6 .

 

[haruspex]

$a_x = asin \phi$

$a_y = acos \phi$
Why ?

This is what you objected to in post#6 .

There is a difference between entirely and principally.

 

[Vibhor]

Should it be

Along x -direction , $T - \mu mgcos \theta sin \phi = masin \phi$

Along y-direction , $\mu mgcos \theta cos \phi -mgsin \theta = macos \phi$ ??

 

[TSny]

Vibhor,
To simplify the notation, use some symbol such as $f$ to stand for the constant $mgsinθ$.
Can you write the magnitude of the friction force in terms of $f$ ? Remember that the angle of the incline is set at a special value so that $\tan \theta = \mu$.

 

[Vibhor]

Vibhor,
To simplify the notation, use some symbol such as $f$ to stand for the constant $mgsinθ$.
Can you write the magnitude of the friction force in terms of $f$ ? Remember that the angle of the incline is set at a special value so that $\tan \theta = \mu$.

Let $W = mgsinθ$ and $f$ represents magnitude of friction , then $f =W$

 

[TSny]

Right, so the friction force and the weight along the incline can both be represented by the symbol $f$. Then, your force equations for the x and y directions can be expressed in terms of just $f$ and $T$.

 

[Vibhor]

Do you think equations in post#15 are correct ?

Edit : I am still not sure about the direction of friction .

 

[TSny]

Do you think equations in post#15 are correct ?

Edit : I am still not sure about the direction of friction .

I think the case where the particle is located horizontally from the hole is kind of a special case. At this point the particle is on the verge of slipping without any tension force. So, you can deduce the direction of the friction force here by just considering the weight and friction alone.

If I am working it correctly, the motion when the particle is higher on the plane than the hole is different than the motion when the particle is lower on the plane than the hole. So, the special case where the particle is located horizontally from the hole is a transition point between the two types of motion. I also don't think you need to worry about putting acceleration into your equations. As the problem says, consider static equilibrium conditions at each point just before slipping to determine which way the particle will move for the next infinitesimal step.

Hope I'm not butting in and redirecting the discussion. My intention was just to tidy up the notation in the equations. I always find that to be helpful.

 

[Nidum]

Friction force can only have one line of action .This is the line of action which opposes motion against the resultant of all forces trying to cause motion .

So the friction force in this problem acts along the line of the resultant of the string tension and the gravity force component and acts in the sense which opposes motion .

If motion does occur then the direction of motion is along the line of the resultant of the two forces .

The above is for a perfect model and very slow speed motion .

In a real embodiment of this problem with the usual imperfections the motion would probably be quite unpredictable and different each time of doing the experiment .

Motion would become more predictable if string tension was allowed to be large enough to cause some acceleration of the particle and cause it to move with increasing but definite velocity .

 

[Vibhor]

I also don't think you need to worry about putting acceleration into your equations.As the problem says, consider static equilibrium conditions at each point just before slipping to determine which way the particle will move for the next infinitesimal step.

Let $\phi$ represent the angle which string makes with the y-direction (upslope +ve)

Applying Lami's theorem and resolving forces ,

Along x-direction $fsin(180° - 2\phi) = Tsin\phi$

Along y-direction $W = Tcos\phi + fcos(180° - 2\phi)$

Is that correct ??

 

[TSny]

Let me make sure I understand your coordinate system. Origin is at the hole, x-axis horizontal to the right, y-axis upward along the slope. $\phi$ is angle between positive y-axis and string. Not sure if $\phi$ is measure positive in the CW direction or CCW direction. Also, not sure which quadrant you have placed the particle.

A diagram showing your conventions would be nice.

I believe the case where the particle is above the x-axis is different than the case where the particle is below the x axis. So, I suggest treating the cases separately and dealing first with the case where the particle is above the x axis.

 

[Vibhor]

Let me make sure I understand your coordinate system. Origin is at the hole, x-axis horizontal to the right, y-axis upward along the slope. $\phi$ is angle between positive y-axis and string. Not sure if $\phi$ is measure positive in the CW direction or CCW direction. Also, not sure which quadrant you have placed the particle.

A diagram showing your conventions would be nice.

I believe the case where the particle is above the x-axis is different than the case where the particle is below the x axis. So, I suggest treating the cases separately and dealing first with the case where the particle is above the x axis.

Origin is at the hole, x-axis horizontal to the right, y-axis upward along the slope. $\phi$ is angle between positive y-axis and string. $\phi$ is measured positive in the CCW direction. Particle is in second quadrant , I guess (case where the particle is above the x axis)

Should I apply Lami's theorem ?

 

[TSny]

Origin is at the hole, x-axis horizontal to the right, y-axis upward along the slope. $\phi$ is angle between positive y-axis and string. $\phi$ is measured positive in the CCW direction.

In which quadrant is the particle?

Should I apply Lami's theorem ?

Had to look that up. You can probably make use of this theorem for the second case where the particle is below the x axis. But you can get by without it.

 

[Vibhor]

In which quadrant is the particle?

Second .

But you can get by without it.

How should I approach ?

 

[TSny]

I think second quadrant is harder than first quadrant. Go with the easier case first. Think about what's going on with no tension in the string and then imagine what happens as you gradually apply tension.

 

[Vibhor]

The picture in OP shows particle to be in second quadrant . Right ?

 

[TSny]

The picture in OP shows particle to be in second quadrant . Right ?

Yes, sorry! You are right to begin with the second quadrant. Then treat the case in the third quadrant.

 

[Vibhor]

Do you think the attached picture correctly represents the forces acting on the particle in second quadrant ? $\phi$ is measured clockwise from y direction .