PDEs greater than order 2 with real world applications?

[BWV]

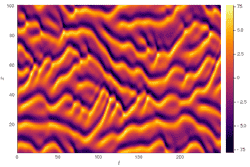
Came across this today, a fourth order PDE - the Kuramoto–Sivashinsky equation, apparently used to model flames

https://en.wikipedia.org/wiki/Kuramoto–Sivashinsky_equation

Any other examples of high order PDEs with actual applications?

 

[anuttarasammyak]

You will find it in non linear physics e.g. KdV soliton https://en.wikipedia.org/wiki/Korteweg–De_Vries_equation

 

[jasonRF]

Another example is one dimensional transverse waves on a uniform slender beam, which satisfy $u_{xxxx} + a^2 \, u_{tt} = 0$. This is a special case of the Euler-Bernoulli equation
https://en.wikipedia.org/wiki/Euler–Bernoulli_beam_theory