Perfectly inelastic collision between Projectile and a hinged disk

[Thermofox]

Homework Statement

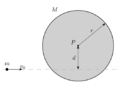
A disk of mass $M=2kg$ and radius $r = 20 cm$, is arranged vertically and fixed to a pin, $P$, around which it can rotate without friction. A projectile, to be considered as a point of mass, has a mass of $m =100 g$. Initially it has a constant velocity, $v_0$. Then the projectile hits the disk. The collision is completely inelastic. $d =10 cm$ is the distance between the point of collision and the axis of the disk.

Relevant Equations

$\Sigma \tau= I \alpha$

I'm asked to find 2 things:
1) The minimum value of the velocity $v_0$ that allows $m$
to complete a full revolution around the disk
2) the value of the pulse provided by the pin to the disc at the moment of impact.

My thinking:
I don't understand why the problem asks me to find a minimum velocity. If the disk can rotate without friction what opposes to its rotation? Shouldn't it continue to rotate, indefinitely? Shouldn't it conserve its kinetic rotational energy?
There is a conservation of angular momentum, but not linear momentum because there is the reaction of the pin, which is an external force.
I assume the motion of the rotation to be uniformly accelerated => $\theta (T) = \theta_{i} + \omega_i T + \frac 1 2 \alpha T^2$ ; $2\pi= \frac 1 2 \alpha T^2$, where $T$ is the time it takes to do a revolution.
For point 2 maybe, since the pulse, $I$, is generated only by the pin => $I= \Delta P$?

 

[kuruman]

Is there a figure that goes with this? If so, please post it. If not, you need to tell us where on the disc is point P relative to the disc axis. The minimum velocity depends on this information.

Also, your assumption that the acceleration is constant is incorrect. The physical situation is the same as a ballistic pendulum, except that the pendulum bob is a disc instead of a point mass.

 

[Thermofox]

Is there a figure that goes with this? If so, please post it. If not, you need to tell us where on the disc is point P relative to the disc axis. The minimum velocity depends on this information.

Also, your assumption that the acceleration is constant is incorrect. The physical situation is the same as a ballistic pendulum, except that the pendulum bob is a disc instead of a point mass.

I'm so sorry, I always forget to post the figure.

 

[kuruman]

Thank you for the figure. You are to assume that gravity acts from the top of the screen to the bottom. The system of embedded projectile plus disc is in equilibrium when the bullet is directly below the center of the disc at P. Describe the motion of the disc + bullet system immediately after the collision. Will the disc make a full revolution no matter how small the speed of the projectile?

 

[Thermofox]

Will the disc make a full revolution no matter how small the speed of the projectile?

Now I see that gravity also acts on the embedded bullet. Thus it causes a torque $\vec {\tau_m}= \vec {r_p} \times \vec {F_{m,g}}$ that opposes to the torque generated by the collision. So the torque generated by the collision must be high enough to overcome $\vec {\tau_m}$ for half of a revolution.

Describe the motion of the disc + bullet system immediately after the collision.

If I call the angular momentum $L$ => $\Delta L =0$,
$L_{\text{before impact}}= m v_0 d \sin(90°)= m v_0d$
$L_{\text {after impact}}= I_{tot} \omega = (I_p + I_m) \omega$
=> $m v_0d=(I_p + I_m) \omega$

 

[haruspex]

Now I see that gravity also acts on the embedded bullet. Thus it causes a torque $\vec {\tau_m}= \vec {r_p} \times \vec {F_{m,g}}$ that opposes to the torque generated by the collision. So the torque generated by the collision must be high enough to overcome $\vec {\tau_m}$ for half of a revolution.

There is no continuing torque from the collision. That is a one-off event causing an angular momentum for the disc+bullet system.
The torque opposing that, caused by gravity on the bullet, will change as the disc rotates. This makes it rather complicated to figure out whether it will be enough to stop the rotation before the bullet reaches the top.
What other approach can you think of?

 

[Thermofox]

There is no continuing torque from the collision. That is a one-off event causing an angular momentum for the disc+bullet system.
The torque opposing that, caused by gravity on the bullet, will change as the disc rotates. This makes it rather complicated to figure out whether it will be enough to stop the rotation before the bullet reaches the top.
What other approach can you think of?

$m$ will be able to complete a revolution if it manages to make half a revolution, so when $m$ reaches the top. Therefore the minimum requirement is for $m$ to reach the top.
Energetically this happens when all of the kinetic rotational energy gets transformed into potential gravitational energy => if I set that $U=0$ at P, I then have that: $\frac 1 2 I_p \omega^2 - mgd = mgd$.
With this condition when $m$ reaches the top, there should be no kinetic rotational energy. I don't know if this means that the disk will stop rotating the moment $m$ reaches the top, but I feel like, since this is an unstable equilibrium, the disk will continue rotating even though $\omega_{top}=0$

 

[haruspex]

$m$ will be able to complete a revolution if it manages to make half a revolution, so when $m$ reaches the top. Therefore the minimum requirement is for $m$ to reach the top.
Energetically this happens when all of the kinetic rotational energy gets transformed into potential gravitational energy => if I set that $U=0$ at P, I then have that: $\frac 1 2 I_p \omega^2 - mgd = mgd$.

Ok, but how are you defining $I_p$? Are you being consistent about that between posts #5 and #7?

With this condition when $m$ reaches the top, there should be no kinetic rotational energy. I don't know if this means that the disk will stop rotating the moment $m$ reaches the top, but I feel like, since this is an unstable equilibrium, the disk will continue rotating even though $\omega_{top}=0$

You don't need to worry about the case where it is exactly the right energy to reach the top. There is no exact equality of such things in the real world.

 

[Thermofox]

Ok, but how are you defining $I_p$? Are you being consistent about that between posts #5 and #7?

You are right, I should've written $I_{tot}= I_p + I_m = \frac 1 2 M r^2 + md^2$. Now I need to determine $\omega$ in terms of $v_{0,min}$. To do that I can use the conservation of angular momentum I did on post #5: $$m v_0d=(I_p + I_m) \omega \Rightarrow \omega = \frac {mv_0d} {(I_p + I_m)}= \frac {mv_0d} {I_{tot}}$$ Hence $\frac 1 2 I_{tot} \frac {mv_{0,min}d} {I_{tot}} - mgd = mgd$ => $v_{0,min}= \frac {2mgd (2)} {md}= 4g$.

For point 2, the collision generates an impulse. Thus $P$ will counteract that impulse, with another impulse, so that the disk remains fixed. Does this mean that the impulse generated by $P$ is, $I = \Delta P = P_{\text{after impact}} - P_{\text{before impact}} = 0 - mv_0$?

 

[haruspex]

Hence $\frac 1 2 I_{tot} \frac {mv_{0,min}d} {I_{tot}} - mgd = mgd$ => $v_{0,min}= \frac {2mgd (2)} {md}= 4g$.

Some dimensionality problems there.
You forgot to square $\omega$, and you end up with a velocity equal to an acceleration.

 

[Thermofox]

Some dimensionality problems there.
You forgot to square $\omega$, and you end up with a velocity equal to an acceleration.

$\frac 1 2 I_{tot} (\frac {mv_{0,min}d} {I_{tot}})^2 - mgd = mgd$ => $v_{0,min}=\sqrt {\frac {2mgd (2)(I_{tot)}} {m^2d^2}}$

 

[haruspex]

$\frac 1 2 I_{tot} (\frac {mv_{0,min}d} {I_{tot}})^2 - mgd = mgd$ => $v_{0,min}=\sqrt {\frac {2mgd (2)(I_{tot)}} {m^2d^2}}$

Yes, that looks right, though you could simplify it a little.

 

[Thermofox]

Yes, that looks right, though you could simplify it a little.

I could simplify $md$ at the numerator with $m^2d^2$ at the denominator.

For point 2, the collision generates an impulse. Thus $P$ will counteract that impulse, with another impulse, so that the disk remains fixed. Does this mean that the impulse generated by $P$ is, $I = \Delta P = P_{\text{after impact}} - P_{\text{before impact}} = 0 - mv_0$?

Do you think it is correct?

 

[haruspex]

I could simplify $md$ at the numerator with $m^2d^2$ at the denominator.


Do you think it is correct?

All except the last step. The disc+bullet still has some linear momentum just after impact.
It will continue to change after impact, though.

 

[Thermofox]

The disc+bullet still has some linear momentum just after impact.

So the disk+bullet has a linear velocity? Doesn't it remain still?

 

[haruspex]

So the disk+bullet has a linear velocity? Doesn't it remain still?

You know it rotates. Do you mean the mass centre stays still? Where is the mass centre?

 

[Thermofox]

You know it rotates. Do you mean the mass centre stays still? Where is the mass centre?

Ohh now I see it. It's shifted downwards, therefore it is moving. Does this mean that $v_{cm}= \omega d$?

 

[haruspex]

Ohh now I see it. It's shifted downwards, therefore it is moving. Does this mean that $v_{cm}= \omega d$?

That would be the velocity of the bullet, not of the mass centre of disc+bullet.
But which do you need to find the change in linear momentum?

 

[Thermofox]

That would be the velocity of the bullet, not of the mass centre of disc+bullet.
But which do you need to find the change in linear momentum?

I think I should be interested in the linear momentum of the mass centre

 

[haruspex]

I think I should be interested in the linear momentum of the mass centre

My tip is to avoid finding mass centres if you can. It is almost always easier to find whatever attribute you are interested in - momentum, angular momentum, moment of inertia, mass - of each object separately then add.

 

[Thermofox]

My tip is to avoid finding mass centres if you can. It is almost always easier to find whatever attribute you are interested in - momentum, angular momentum, moment of inertia, mass - of each object separately then add.

Ok, I'll keep that in mind. So I should determine the linear momentum of the disk, the linear momentum of the bullet and then add them together. $P_{disk}= M\omega r$ ; $P_{bullet}= m\omega d$.
Therefore $\Delta P= I \Rightarrow (M\omega r + m\omega d) - (mv_0)= I$

 

[haruspex]

$P_{disk}= M\omega r$

Is the mass centre of the disc moving?

; $P_{bullet}= m\omega d$.

Yes.

 

[Thermofox]

Is the mass centre of the disc moving?

No, so $P_{disk}=0$.
It makes sense because the centre of mass overlaps with the axis of rotation, thus $P_{disk}=M\omega R$, where R is the distance between the axis of rotation and the centre of mass which is $0 \Rightarrow P_{disk}= M \omega \space 0 = 0$.
Which means that $m\omega d - mv_0 = I$

 

[kuruman]

Which means that $m\omega d - mv_0 = I$

Shouldn't one of these masses be $M$?

 

[Thermofox]

Shouldn't one of these masses be $M$?

What I did is $P_{\text {after impact}} - P_{\text {before impact}} = (P_{disk} + P_{bullet,embedded}) - (P_{bullet})= 0 + m\omega d - mv_0$.

 

[kuruman]

OK.

 

[haruspex]

No, so $P_{disk}=0$.
It makes sense because the centre of mass overlaps with the axis of rotation, thus $P_{disk}=M\omega R$, where R is the distance between the axis of rotation and the centre of mass which is $0 \Rightarrow P_{disk}= M \omega \space 0 = 0$.
Which means that $m\omega d - mv_0 = I$

Right.