Plotting the approximation of the Dirac delta function

[Lambda96]

Homework Statement

Plot $g^{\epsilon}(x)$ for $\epsilon=1$ , $\epsilon=\frac{1}{2}$ and $\epsilon=\frac{1}{4}$

Relevant Equations

none

Hi,

I am not sure if I have solved the following task correctly

I did the plotting in mathematica and got the following

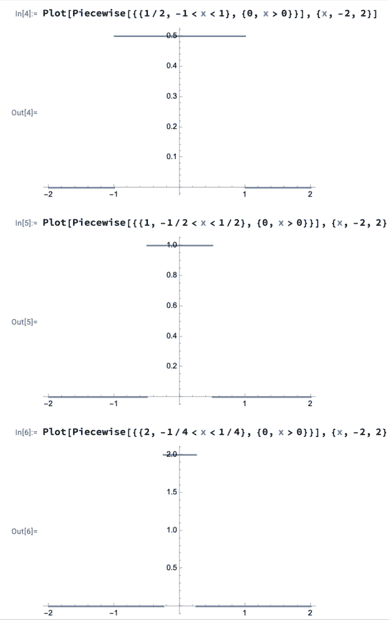
Would the plots be correct? What is meant by check for normalization, is the following meant?

For the approximation for $\epsilon > 0$, does it mean that for the area of $0 < x < \epsilon$ the area must be 1, so for the case $\epsilon=1$ the total area would be 1, the half for $0 < x < \epsilon$ would then be $\frac{1}{2}$, so the normalization constant should be 2?

 

[scottdave]

To sketch usually means to draw by hand. Is this behavior that you expected? Look at the formula. Between minus epsilon and +epsilon, what is the function doing (does it change with x)?

Normalization refers to the area under the "curve" equal to 1 over the entire spectrum. Do these graphs satisfy that?

 

[FactChecker]

Would the plots be correct?

Yes, those plots look correct.

What is meant by check for normalization, is the following meant?

It means to check that the integral is 1.

For the approximation for $\epsilon > 0$, does it mean that for the area of $0 < x < \epsilon$ the area must be 1,

No. It means that the area of $- \epsilon < x < \epsilon$ must be 1.

so for the case $\epsilon=1$ the total area would be 1, the half for $0 < x < \epsilon$ would then be $\frac{1}{2}$, so the normalization constant should be 2?

No. No further normalization is needed. The area between each graph and the x axis is already 1.

 

[Lambda96]

Thank you scottdave and FactChecker for your help