Potential Energy formula in Special Relativty

[pervect]

In order to do a simple check of the proposed energy formula, I decided to consider a simple case. Suppose we set up an accelerating frame, based on a reference rocket acclelerating at 1 light year/year^2, approximately 9.5 meters/second^2. What velocity do we need to launch a projectile at in order to reach a "height" of 1 light years above our reference rocket?

This is an example of geometric units. We measure all distances in light years, and all times in years. As a consequence, the numerical value of "c" is 1, as is the numerical value of "a".

We predict from the formula that $dx/d\tau$ must equal $\sqrt{3}$ for an object to have the same energy as an object moving with $dx/d\tau=0$ at a height of 1. At a height of 1, $\gamma_g = 1+ax/c^2 = 1+1 = 2$, meaning an object at that height has twice its rest energy.

In order for $dx/d\tau$ to be $\sqrt{3}$, we find $v = dx/dt = \sqrt{3}/2$ , giving $dx/d\tau$ = (dx/dt) \, (dt/d$\tau$) = $\sqrt{3}$.

Here's the plot I did on a Rindler chart. The chart charts the course of the two rockets, our reference rocket starting at d=1, and a second rocket 1 light year "higher" in the accelerated frame. These plots are done in the inertial frame co-moving with the rockets at t=0.

These two rockets are plotted on the graph in black. The projectile launched at a velocity of $\sqrt{3} / 2$ follows a straight line inertial trajectory of $d = \frac{\sqrt{3}}{2}\,t+1$, plotted in green.

The plot confirms the prediction. The green line representing the launched projectile just catches up to the black line of the higher rocket.

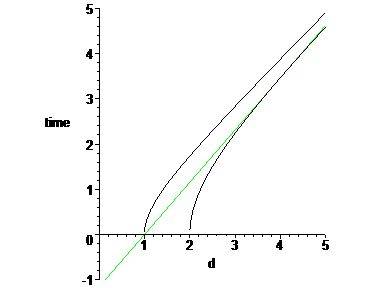
The equations are fairly simple if one wants to go into more depth. The reference rocket follows a hyperbola $d^2-t^2=1$. The rocket one light year above the reference rocket follows a hyperbola of $d^2-t^2 = 4$. There are various articles on "hyperbolic motion" that should explain this more - I'm not going to look for any further references unless there are questions. The green line does indeed meet the black line at d=4, t=$2 \,\sqrt{3}$

 

[PeterDonis]

Here is proper time.

Actually, for the observer at $x = 1 / \alpha$ in Rindler coordinates, the observer's proper time is the same as Rindler coordinate time (since this observer has no time dilation in Rindler coordinates). So in the approximation you are using for your energy formula, Rindler coordinate time can be substituted for proper time.

 

[pervect]

Actually, for the observer at x=1/α in Rindler coordinates, the observer's proper time is the same as Rindler coordinate time (since this observer has no time dilation in Rindler coordinates). So in the approximation you are using for your energy formula, Rindler coordinate time can be substituted for proper time.

I don't think this is true.

For instance, a clock near the Rindler horizon will be ticking much differently than the coordinate time there. In general one needs to calculate $d\tau$ from the line element.

The formula for energy was originally derived in Rindler line eleement, but when we modified the energy formula to

$$E = \left(1 + \frac{a\,x}{c^2} \right) \sqrt{1 + \left( \frac{1}{c} \frac{dx}{d\tau} \right)^2}$$

(which I do prefer) the line element in the accelerated coordinate system (t,x,y,z) becomes:

$$ds^2 = -c^2\,d\tau^2 = -(c^2 + a^2\,x^2) dt^2 + dx^2 + dy^2 + dz^2$$
or with the +--- convention, which may be easier for this case,

$$d\tau^2 = (1+ a^2\,x^2 / c^2)dt^2 - \frac{1}{c^2} (dx^2 + dy^2 + dz^2)$$

 

[pervect]

I had a few more thoughts.

First of all I wanted to give an overview of the concepts used to derive the energy I worked on earlier, formula, now that I'm reasonably hapy with said formula. Previously, I had simply suggested that it was similar to methods used to calculate the energy of test masses orbiting in the Schwarzschild geometry of GR without giving more details.

The basic idea behind the calculation is Noether's theorem. Noether's theorem says, roughly speaking, that a conserved energy is associated with a time-translation symmetry. Fun historical fact - it was concerns over the concept of energy in General Relativity raised by Hilbert, Felix Klein, and others that led to the development of the theorem. It's quite an interesting story, also interesting is the sexism that Noether had to deal with in her everyday work, such as not being able to lecture or be paid for her work by the university.

The time-translation symmetry in this case is the time-translation symmetry of the metric. So writing down the metric (or line element) allows us to calculate the energy simply from the time-translation symmetry associated with it. Well, perhaps the details get a bit complex, but the idea is simple.

A notable feature of the energy relation is that the energy - including the rest energy - goes to zero at the Rindler horizion, where (1+ax/c^2) goes to zero. And below that, it goes negative. What does this mean, physically? My argument is that it means that the concept of an accelerated frame is breaking down at the Rindler horizon. Certainly there are problems about thinking of an object "at rest" at said horizon, it's a null surface. Light could have a constant Rindler coordinate, but it cannot meaningfully be said to be "at rest".

Furthermore, I will go so far as to suggest that since the expression for energy basically only depends on the existence of the time translation symmetry, any sort of coordinates that describe an accelerated frame that explicitly have this symmetry are going to experience similar problems. It has been suggested that there may be a way around this. I suppose I can't absolutely rule out the possibility, but I won't be convinced that there is a way around the issue, which I have called a size constraints on the size of an acclerated frame, until I see a well-behaved line element associated with such a frame. So far, we haven't seen any such thing.

 

[PeterDonis]

a clock near the Rindler horizon will be ticking much differently than the coordinate time there

I meant the observer at $x = 1 / \alpha$ in your original formulation, where the Rindler horizon is at $x = 0$. In the revised formulation I gave, which you have now adopted, this observer is at $x = 0$, and the Rindler horizon is at $x = - c^2 / a$.

 

[Sagittarius A-Star]

$$d\tau^2 = (1+ a^2\,x^2 / c^2)dt^2 - \frac{1}{c^2} (dx^2 + dy^2 + dz^2)$$

In the first term of the right side of the equation I see an issue with units plausibility check (1+ ...). When I compare to the book "Lecture Notes on the General Theory of Relativity" from Gron, equation (4.47), also a square is missing there.

Proposal:
$$d\tau^2 = (1+ a\,x / c^2)^2dt^2 - \frac{1}{c^2} (dx^2 + dy^2 + dz^2)$$
From that, he derives a time dilation formula.

 

[kent davidge]

I thought it was just a counter example to the claim that non-inertial coordinates only cover part of Minkowski space. So nothing particularly practical.

You say this, but the mentioned coordinates (Born) were shown to be singular at $r = 0$. So let me ask: when you physicists say that a coordinate system covers all of spacetime, is it fine to neglect a single pole like the one in this case?

 

[vanhees71]

Well, the coordinate singularity of Born coordinates at $r=0$ are really not an issue. You can simply reintroduce "Cartesian coordinates" via $x=r \cos \varphi$, $y=r \sin \varphi$, and you have a singularity free chart everywhere. From a mathematical point of view it's a chart over all spacetime.

If you want to describe observers by worldlines given by three of the coordinates held fixed and the fourth to be used as the time coordinate, you are restricted to the cylinder $\omega r<1$. Then $t$ is the time coordinate of course. At $\omega r=1$ you have a light-like curve, and for $\omega r>1$ the coordinate lines are all spacelike.

 

[Ibix]

You say this, but the mentioned coordinates (Born) were shown to be singular at $r = 0$.

Fair point. Examples without this issue are available - simply define $x'=x-x_0\sin(t/t_0)$ and otherwise keep Einstein coordinates. Or you could use radar coordinates based on a non-inertial but not eternally accelerating worldline, if you prefer a less contrived example.

 

[vanhees71]

In the first term of the right side of the equation I see an issue with units plausibility check (1+ ...). When I compare to the book "Lecture Notes on the General Theory of Relativity" from Gron, equation (4.47), also a square is missing there.

Proposal:
$$d\tau^2 = (1+ a\,x / c^2)^2dt^2 - \frac{1}{c^2} (dx^2 + dy^2 + dz^2)$$
From that, he derives a time dilation formula.

I think Rindler coordinates can be introduced most easily by defining it via a congruence of time-like world lines, considering points in constant proper acceleration along the $x$ axis of a Minkowski coordinate system $(t,x,y,z)$ with the world-line element
$$\mathrm{d}s^2=\eta_{\mu \nu} \mathrm{d}x^{\mu} \mathrm{d}^{\nu}=\mathrm{d} t^2-\mathrm{d} \vec{x}^2,$$
using natural units with $c=1$. In the following we only need to consider the $(t,x)$ plane, because in the change to Rindler coordinate nothing happens with $y$ and $z$. So we can set the corresponding new coordinates simply $y=\eta$ and $z=\zeta$.

Then the congruence of timelike world lines in the planes parallel to the $tx$ plane is defined by the EoM. of observers starting with 0 velocity at $x=\xi$. The solution in terms of a convenient affine parameter $\lambda$ is
$$t=\xi \sinh(\lambda \alpha), \quad x=\xi \cosh(\lambda \alpha).$$
That it's indeed an affine parameter is easily seen from
$$\dot{t}^2-\dot{x}^2=(\xi \alpha)^2,$$
and indeed $\lambda$ is the proper time of the observer on the worldline starting at $\xi=1/\alpha$.
The line element in the Rindler coordinate $(\lambda,\xi,\eta,\zeta)$ is
$$\mathrm{d} s^2 =\xi^2 \alpha^2 \mathrm{d} \lambda^2-\mathrm{d} \vec{x}^{\prime 2}$$
with $\vec{x}'=(\xi,\eta,\zeta)$.
The alternative form mentioned in #76 is also correct. It just defines $\xi$ differently with the initial point of the congruence of uniformly accelerated observers at $x=0$:
$$t=(1/\alpha +\tilde{\xi}) \sinh(\alpha \lambda), \quad x=(1/\alpha+\tilde{\xi}) \cosh(\alpha \lambda)-1/\alpha$$
leading to the mentioned line element
$$\mathrm{d} s^2=(1+\alpha \tilde{\xi})^2 \mathrm{d} \lambda^2-\mathrm{d} \tilde{x}^2$$
where $\tilde{x}^2=(\tilde{\xi},\eta,\zeta)$.

 

[pervect]

In the first term of the right side of the equation I see an issue with units plausibility check (1+ ...). When I compare to the book "Lecture Notes on the General Theory of Relativity" from Gron, equation (4.47), also a square is missing there.

Proposal:
$$d\tau^2 = (1+ a\,x / c^2)^2dt^2 - \frac{1}{c^2} (dx^2 + dy^2 + dz^2)$$
From that, he derives a time dilation formula.

Good catch. I'm pretty sure your psoposal is correct - I'll doulbecheck in the morning, if I remember.

 

[pervect]

In the first term of the right side of the equation I see an issue with units plausibility check (1+ ...). When I compare to the book "Lecture Notes on the General Theory of Relativity" from Gron, equation (4.47), also a square is missing there.

Proposal:
$$d\tau^2 = (1+ a\,x / c^2)^2dt^2 - \frac{1}{c^2} (dx^2 + dy^2 + dz^2)$$
From that, he derives a time dilation formula.

I looked it up - MTW uses a similar line element, but in geometric units. And you're right. There's a simpler argument for why you're right though that doesn't need to be looked up.

Basically, the metric coefficient is $-\gamma_g^2 \, dt^2$. This follows directly from the concept of gravitational time dilation . $\gamma_g$ used to be $\alpha x$ in the (geometrized) Rindler coordinates, and the point at which the factor $\gamma_g$ was unity was at $x=1/\alpha$. With the new coordinates, $\gamma_g = 1 + ax/c^2$ and $\gamma_g$ is unity at x=0.

 

[Sagittarius A-Star]

$$d\tau^2 = (1+ a\,x / c^2)^2dt^2 - \frac{1}{c^2} (dx^2 + dy^2 + dz^2)$$

With the new coordinates, $\gamma_g = 1 + ax/c^2$ and $\gamma_g$ is unity at x=0.

Yes. Gron derives in his book the following equation (4.50):
$$d\tau = dt\sqrt {(1+ \frac{g\,x} {c^2})^2 - \frac{v^2}{c^2}}$$
This expresses the combined effect of the gravitational and the kinematic time dilation.

• While the traveling twin travels inertially, then $g=0$ and the left term under the square root is "1". That gives the normal time-dilation formula for inertial frames.
• While traveling accelerated, then $g\neq 0$ and the right term under the square root can be neglected for the influence on age difference, if the turnaround-time is defined to be arbitrarily small compared to the inertial travel times.