Practical measurements of rotation in the Kerr metric

[PeterDonis]

In other words, this definition of ring non-rotation seems to require more physics than just the physics of the given ring that we wish to analyze (the properties of space-time itself included in the physics of the given ring of course).

I think this is correct; although Malament never explicitly states it, I think it's implicit in his definition of a "striated orbit cylinder" that the coefficient $k$ that appears in the 4-velocity field is constant. (One piece of indirect evidence for this is that he wants the ring to be in a state of "rigid" rotation; but for the striated orbit cylinder congruence to be rigid, $k$ must be constant. Even though technically the value of $k$ off of the cylinder is never "sampled" by any member of the congruence, it still is required, as you note, to evaluate derivatives.)

In the later discussion of the "relative rotation criterion" for different rings, Malament does allow for the possibility of different rings having different values of $k$; rings of ZAMOs at different values of $r$ could be treated using the method he uses there. But that method would treat rings of ZAMOs at different $r$ as belonging to different congruences (different striated orbit cylinders). I don't think his methods would work if you tried to treat all ZAMO rings (at different values of $r$) as members of the same congruence.

 

[WannabeNewton]

Thanks Peter!

 

[yuiop]

Can I conclude from all the above, that a ZAMO ring in the Kerr metric is not rotating by the ZAM criterion (Sagnac effect) but generally speaking does not qualify as not rotating by the CIR criterion? In other words, a gyroscope that is fixed by a suitable gimble to a Kerr ZAMO ring (so that it remains untorqued) so that it is initially tangential to the ZAMO ring, will not remain tangential to the the ZAMO ring, as a general rule. Furthermore, it seems other than satisfying the ZAM criterion, there is nothing special about gyrosopes attached to a ZAMO ring in the Kerr metric, such as remaining pointed at a fixed point at infinity or any other readily identifiable reference point.

 

[WannabeNewton]

Yes.

By the way, I just remembered the existence of another paper of Malament's in which the relative angular velocity of two neighboring observers is discussed in much more detail. Note that Malament starts out by using telescopes and null geodesics (light beams) to define a unit direction vector representing the orientation of the telescope between the two neighboring observers and then relates the angular velocity of the telescope (i.e. the relative angular velocity of the two neighboring observers) to the "cross product" of the unit direction vector with its Fermi-derivative, which physically is just the rotation of the telescope relative to a local compass of inertia (mutually orthogonal gyroscope axes). This is a general relationship that holds for all space-times.

Only then does Malament specializes to two neighboring observers following orbits of a time-like Killing field with the aim of relating the angular velocity of the telescope to the vorticity of the time-like Killing field plus a term involving the unit direction vector (which is, importantly, automatically Lie transported by the Killing field). So while the Fermi-derivative definition of relative angular velocity holds true in general cases, it would seem based on the calculations in Straumann's text, Malament's text, and the following paper of Malament's that the strict relationship between the telescope angular velocity and vorticity only holds for time-like Killing fields (which are trivially Born rigid vector fields).

It's a very instructive read albeit the TeX is very awkward: http://philsci-archive.pitt.edu/117/1/RelOrbitalRotation.pdf

 

[yuiop]

It's a very instructive read albeit the TeX is very awkward: http://philsci-archive.pitt.edu/117/1/RelOrbitalRotation.pdf

Thanks for the link. it is fairly lengthy, but it looks interesting so I will digest at my leisure.

I have another question. While Rindler refers to a rigid rotating grid as a reference for his gyroscope equations, other authors seem to calculate the vorticity relative to a (not necessarily rigid) congruence of observers with identical angular velocity. Almost universely, the precession of a gyroscope held by a static observer in the Kerr metric is given as:

$\frac{ma}{r^3(1-2m/r)}$

It is tempting to assume this special case is relative to a rigid grid that is not rotating relative to the distant stars. However, if the precession is relative to a congruence of observers with identical angular momentum, then this assumption is not safe. This is because static observers in the Kerr metric, do not have zero angular momentum, and static observers at different altitudes do not have the same angular momentum. I am having difficulty getting Rindler's equation to agree with other sources so I am wondering if this is due to the differences mentioned above. Unfortunately the rotation of the congruence of equal angular momentum observers is difficult to quantify.

P.S> I sent a PM ;)

 

[yuiop]

This paper http://arxiv.org/pdf/1304.6936v1.pdf probably answers the question in my last post. The paper focuses exclusively on an exact solution for the Lense Thirring precession in various metrics, relative to a reference frame that is stationary with respect to an observer at infinity. Equation (20) when specialised to the equatorial plane is identical to the equation given in the last post. This suggests that when Rindler's equation for the precession is extended to the general case, it should give $\frac{ma}{r^3(1-2m/r)}$ for precession of a gyroscope held by stationary observer in the Kerr metric, when the orbital angular velocity is zero.

 

[WannabeNewton]

This is because static observers in the Kerr metric, do not have zero angular momentum, and static observers at different altitudes do not have the same angular momentum.

I'm not seeing what the issue is. The static observers all have zero angular velocity, that's all that matters when calculating the gyroscopic precession via the vorticity. Angular momentum plays no role here (in fact the angular momentum is more directly related to the Sagnac effect).

Could you pinpoint exactly what in Rindler's paper is troubling you?

 

[yuiop]

I'm not seeing what the issue is. The static observers all have zero angular velocity, that's all that matters when calculating the gyroscopic precession via the vorticity. Angular momentum plays no role here (in fact the angular momentum is more directly related to the Sagnac effect).

I guess I was just distracted by earlier claims that it was the congruence of observers with equal momentum that was significant to vorticity and gyroscope precession. I suspect that angular momentum does play a role here. The fact that observers with zero angular velocity in the Kerr metric do not have equal angular momentum, is directly related to why gyroscopes precess relative to stationary observers in the Kerr metric and not relative to stationary observers in the Schwarzschild metric. The gyroscopes are acting like the paddle wheel that measures the local angular momentum of a fluid vortex. Perhaps I am just clutching at straws trying to make sense of a few things in the Rindler paper. It would certainly help if you could provide some technical assistance with the question I raised in post 56 of the parallel thread.

Could you pinpoint exactly what in Rindler's paper is troubling you?

I think there a few typos in the paper that were throwing me off balance. Perhaps you could check them out. He states in equation (37) that the precession is approximated by $3 \pi m /r$ and that due to the positive sign, the precession is prograde and the Thomas precession is in the opposite sense to the Minkowski case. If you carry out the series approximation, it seems he has the sign wrong for (37). It is easy to see that $-( \gamma \omega-\omega)$ is negative and retrograde. Perhaps this is the source of that myth.

In equation (16) he gives the geodesic orbital angular velocity as:

$\omega = \frac{1}{a\pm \sqrt{r^3/m}}$

If we assume a negative value for $\omega$ represents a retrograde orbit then for fixed r and m, an increasing value of ($a$) results in the retrograde orbital speed increasing which is the opposite of what you would expect. For the prograde orbit an increasing value of ($a$) results in a slowing down of the prograde orbit which again is the opposite of expectations. I suspect the formula should actually be:

$\omega = \frac{-1}{a\pm \sqrt{r^3/m}}$

It might seem a small typo, but when $\omega$ is inserted into the precession equations it does not result in a simple reversal of the sign of the precession. With this correction, the magnitude of precession of the gyroscope $\sqrt{m/r^3}$ in the rest frame of the rotating lattice is no longer the same in both the Schwarzschild and Kerr cases as he claims.

Lastly he states below equation (44) that the precession of gyroscope held by a stationary observer in the Kerr metric is:

$-ma \Delta t \sqrt{1-2m/r}$

when most other sources give the result as:

$\frac{-ma\Delta t}{r^3 \sqrt{1-2m/r}}$

 

[WannabeNewton]

It would certainly help if you could provide some technical assistance with the question I raised in post 56 of the parallel thread.

I think Peter would be able to help you much more efficiently than I for that because he has access to computational tensor algebra software that I don't unfortunately. Sorry about that.

I think there a few typos in the paper that were throwing me off balance. Perhaps you could check them out.

I have class right now but I will definitely scrutinize the calculations in just a couple of hours. Cheers.

 

[Bill_K]

This suggests that when Rindler's equation for the precession is extended to the general case, it should give $\frac{ma}{r^3(1-2m/r)}$ for precession of a gyroscope held by stationary observer in the Kerr metric, when the orbital angular velocity is zero.

This agrees with the result in my blog post,

Ω = γ²ω[r - 3M(1 - aω)]/r + γ²Ma(1 - aω)²/r³
γ² = (1 - (r² + a²)ω² - 2M(1 - aω⁾²/r)^-1

in the nonrotating case, ω = 0.

 

[WannabeNewton]

The fact that observers with zero angular velocity in the Kerr metric do not have equal angular momentum, is directly related to why gyroscopes precess relative to stationary observers in the Kerr metric and not relative to stationary observers in the Schwarzschild metric.

From here on out I'm going to drop the qualifier "natural" when I say "rest frame" since it's understood from context. The reason gyroscopes precess relative to the rest frame of static observers in Kerr space-time is the non-vanishing vorticity of the time-like Killing field $\xi^{\mu}$ in Kerr space-time; in Schwarzschild space-time the vorticity of the time-like Killing field vanishes and so gyroscopes don't precess relative to the rest frames of static observers in this space-time. After all, the formula for the gyroscopic precession is given solely in terms of the vorticity of the time-like Killing field.

More specifically it's given by $\Omega^{\mu}_{\text{gyro}} = -\frac{1}{2}(\xi_{\mu}\xi^{\mu})^{-1}\epsilon^{\mu\nu\alpha\beta}\xi_{\nu}\nabla_{\alpha}\xi_{\beta} =-\frac{1}{2}(\xi_{\mu}\xi^{\mu})^{-1}\omega^{\mu}$. In Schwarzschild space-time $\omega^{\mu} = 0$ whereas in Kerr space-time $\omega^{\mu} \neq 0$. On the other hand, the angular momentum (about the rotation axis) of observers following orbits of $\xi^{\mu}$ is given by $L = (-\xi_{\nu}\xi^{\nu})^{-1/2}\psi_{\mu}\xi^{\mu}$ where $\psi^{\mu}$ is the axial Killing field; coincidentally $L = 0$ in Schwarzschild space-time whereas in Kerr space-time $L \neq 0$...or is it really a coincidence?

First off, in Kerr space-time we can easily find examples of time-like Killing fields of the form $\eta^{\mu} = \xi^{\mu} + \omega \psi^{\mu}$, wherein the angular velocity $\omega$ is constant, such that $\omega^{\mu} = \epsilon^{\mu\nu\alpha\beta}\eta_{\nu}\nabla_{\alpha}\eta_{\beta} \neq 0$ but $L = (-\eta_{\nu}\eta^{\nu})^{-1/2}\psi_{\mu}\eta^{\mu} = 0$ so there is definitely no general relationship between angular momentum and vorticity for non-static time-like Killing fields. As such, don't rely on your Newtonian intuitions when it comes to vorticity and angular momentum of non-static time-like Killing fields as they will surely deceive you in Kerr space-time.

With that in mind, let's come back to static observers but in a more general setting. Given any stationary axisymmetric space-time, $L = 0 \Leftrightarrow \omega^{\mu} = 0$ for static observers and this is very easy to see; as always the static observers by definition follow orbits of the time-like Killing field $\xi^{\mu}$ and as before $L = (-\xi^{\nu}\xi_{\nu})^{-1/2}\xi_{\mu}\psi^{\mu}$.

If we choose the coordinate system adapted to the axial and stationary symmetries (e.g. BL coordinates in Kerr space-time) then $L = (-g_{00})^{-1/2}g_{0\phi}$ and $\xi_{\mu} = g_{00}\delta^{0}_{\mu} + g_{0\phi}\delta^{\phi}_{\mu}$ so if $L = 0$ then $\xi_{[\gamma}\nabla_{\mu}\xi_{\nu]} = g_{00}\delta^{0}_{[[\gamma}\delta^{0}_{\nu]}\nabla_{\mu]}g_{00} = 0$ so $\omega^{\mu} = 0$.

Conversely, if $\omega^{\mu} = 0$ then $\xi_{[\gamma}\nabla_{\mu}\xi_{\nu]} = 0$ so there exists a one-parameter family of space-like hypersurfaces $\Sigma_{(t)}$ orthogonal to $\xi^{\mu}$ that foliate space-time. Furthermore $\mathcal{L}_{\xi}\psi^{\mu} = 0$ so combining these two we can choose coordinates $(t,x^1,x^2,\phi)$ for space-time adapted to $\xi^{\mu}$ and $\psi^{\mu}$. Now in these coordinates $\xi^{\mu} = \gamma\nabla^{\mu}t$ since $\xi^{\mu}$ is orthogonal to $\Sigma_{(t)}$ hence $\psi_{\mu}\xi^{\mu} = \gamma g_{\phi \mu}\nabla^{\mu}t = \gamma \delta^{\mu}_{\phi}\nabla_{\mu}t = 0$ therefore $L = 0$.

So at least for static observers in stationary axisymmetric space-times, $L = 0 \Leftrightarrow \omega^{\mu} = 0$ i.e. vorticity is equivalent to angular momentum (about the rotation axis) and therefore your intuition holds true.

 

[yuiop]

This agrees with the result in my blog post,

Ω = γ²ω[r - 3M(1 - aω)]/r + γ²Ma(1 - aω)²/r³
γ² = (1 - (r² + a²)ω² - 2M(1 - aω⁾²/r)^-1

in the nonrotating case, ω = 0.

I am happy to report that Bill's equation also agrees with the result by MTW for the ZAMO case, the geodesic orbit case by Rindler and is algebraically equivalent to the general equatorial equation (35) by Vishveshwara, when the gamma factor is fixed as mentioned in post 57 of the parallel thread.

With some tutoring on notation from WBN, this is how I obtained the result for the ZAMO case from the MTW precession equation:

$\Omega = \frac{1}{2}\sqrt{\frac{g_{\phi\phi}}{|g_{t\phi} - \omega^2 g_{\phi\phi}|}} \left[\frac{\omega_{,\theta}}{p}\epsilon_{\hat r}-\frac{\Delta^{1/2}\omega_{,r}}{p}\epsilon_{\hat \theta}\right]$

where $\Delta = (r^2-2mr+a^2)$. By considering only ZAMOs in the equatorial plane we can set $\omega_{,\theta}=0$,$p=r$ and after inserting the ZAMO orbital velocity $\omega^2 = (-g_{t\phi}/ g_{\phi\phi})^2$ I obtain after some simplification:

$\Omega = \frac{1}{2}\frac{g_{\phi\phi}}{\Delta^{1/2}} \left[-\frac{\Delta^{1/2}\omega_{,r}}{r}\epsilon_{\hat \theta}\right]$

Interpreting $\omega_{,r}$ as $\frac{\partial{}}{\partial{r}}(-\frac{g_{t\phi}}{ g_{\phi\phi}})$ and after carrying out the derivative the result is:

$\Omega = \frac{1}{2}\frac{g_{\phi\phi}}{\Delta^{1/2}} \left[-\frac{\Delta^{1/2}}{r}\left(\frac{-2ma(a^2+3r^2)}{r^2 (g_{\phi\phi})^2}\right)\epsilon_{\hat \theta}\right]$

$\Omega = \frac{ma(a^2+3r^2)}{r^3 (r^2+a^2+2ma^2/r)}\epsilon_{\hat \theta}$

where $\epsilon_{\hat \theta}$ is the unit vector indicating the axis of the resulting precession is orthogonal to the equatorial plane.

The same result (except for the sign) is obtained by inserting the ZAMO velocity into the general equatorial equation (35) by Vishveshwara or Bill's equation. The general equation also agrees with the result of $\sqrt{m/r^3}$ given by Rindler when we enter the geodesic orbital angular velocity $\omega = 1/(a\pm\sqrt{r^3}{m})$ also given by Rindler. None of these results are particularly easy to obtain from the general formulas and required the use of Maple and some manual simplification.

Bill's general equation which is slightly simpler can be expressed as:

$\Omega = \omega\gamma^2 - \omega\frac{3m}{r}(1-a\omega)\gamma^2 +\frac{ma}{r^3}(1-a\omega)^2\gamma^2$

where the first term is the kinematic Thomas precession, the second term is the geodetic precession due the curvature of spacetime around a gravitational body and the third term is the Lense-Thirring precession due the angular velocity (a) of a rotating gravitational body.

$\Omega$ in all the above formulas is the rotation rate of a rigid rotating lattice relative to a set of gyroscopes as measured by an observer at rest with (and co-spinning with) the lattice, so the precession rate of the gyroscopes is actually $-Omega$. The rotation rate $\omega$ of the rigid lattice is measured by the coordinate observer at infinity in the respective metric. The rotating lattice is equivalent to a congruence of observers all with identical angular velocity, (not momentum). To obtain the precession rate of the gyroscopes as measured by the observer at infinity we correct $\Omega$ by the time dilation factor and subtract the result from $\omega$ so that:

$\Omega_{\infty} = \omega -\omega\gamma + \omega\frac{3m}{r}(1-a\omega)\gamma -\frac{ma}{r^3}(1-a\omega)^2\gamma$

Note that setting a=0 gives the expected Schwarzschild precession and setting m=0 gives the expected Minkowski precession. This strongly suggests that the Thomas precession given by the second term is valid in a gravitational field and has the same sign as in flat space, contrary to some claims in the literature.

I have attached a maple worksheet that compares Bill's and Vishveshwara's precession formulas for the ZAMO case.

The hardest part is keeping track of the signs to determine the direction of precession and a lot of the literature is vague on this issue using $\pm$ signs or $\Omega^2$ to duck the issue. The NASA handouts for the direction for the Lense-Thirring precession in the GBP are full of contradictions on the direction. At the moment on balance, based on what is commonaly assumed for the Schwarzschild case, I am going with the L-T precession being retrograde. Also the MTW equation gives the opposite sign for the precession compared to the other equations. If anyone can shed some light on the direction of precession, I would be grateful.

 

[PeterDonis]

The hardest part is keeping track of the signs to determine the direction of precession

My understanding is that, if we are talking about the precession of gyroscopes relative to an observer at infinity, Thomas precession is retrograde, de Sitter (geodetic) precession is prograde, and Lense-Thirring precession is retrograde.

 

[WannabeNewton]

This strongly suggests that the Thomas precession given by the second term is valid in a gravitational field and has the same sign as in flat space, contrary to some claims in the literature.

Could you provide an example of such a contrarian? I don't see why anyone would think that Thomas precession is completely absent in a gravitational field. What they might have said is that it would be hard to interpret such a term as Thomas precession in the same sense as in flat space-time because we don't have a fixed background global inertial frame to apply consecutive Lorentz boosts from.

If anyone can shed some light on the direction of precession, I would be grateful.

Thomas Precession = retrograde
Geodetic Precession = prograde
Lense-Thirring Precession = retrograde

The retrograde nature of Thomas you already have an intuition for. The geodetic precession is just a spin-orbital coupling so we would expect it to be prograde. What may not be immediatly intuitive is the retrograde nature of the Lense-Thirring precession. Ohanian has a nice description of it's physical origin (see attachment). As a side note, Ohanian's book is one of those GR books that you just have to buy.

 

[yuiop]

Could you provide an example of such a contrarian? I don't see why anyone would think that Thomas precession is completely absent in a gravitational field. What they might have said is that it would be hard to interpret such a term as Thomas precession in the same sense as in flat space-time because we don't have a fixed background global inertial frame to apply consecutive Lorentz boosts from.

This is a quote from the Rindler precession paper:

... while one-third is essentially due to Thomas precession; however, the latter is now in the forward rather than the retrograde sense, for it is now the frame of the field that Thomas precesses around the gyroscope, which itself is free, i.e. unaccelerated.

These two image links

http://postimg.org/image/k3ny4zptx/
http://postimg.org/image/wh0sbwfid/

that you posted a while ago, state:

The second term is purely a special relativistic effect (Thomas precession) ... The second term will contribute whenever there is a non gravitational source of acceleration but will vanish for a gyroscope that is in free fall around a massive body.

This is from Wikipedia:

One can attempt to break down the de Sitter precession into a kinematic effect called Thomas precession combined with a geometric effect caused by gravitationally curved spacetime. At least one author[6] does describe it this way, but others state that "The Thomas precession comes into play for a gyroscope on the surface of the Earth ..., but not for a gyroscope in a freely moving satellite."[7] An objection to the former interpretation is that the Thomas precession required has the wrong sign.

[6] Rindler, Page 234
[7] Misner, Thorne, and Wheeler, Gravitation, p. 1118

What may not be immediatly intuitive is the retrograde nature of the Lense-Thirring precession. Ohanian has a nice description of it's physical origin (see attachment).

Ohanian's description for Lense-Thirring precession is very much like the paddle wheel in a fluid vortex analogy.

Did you get a chance to check out the the possible typos in the Rindler paper in post 158 here https://www.physicsforums.com/showthread.php?t=729416&page=9 ?

 

[Mordred]

not sure if this will help you all but I noticed this article contained a lot of the metrics you all are referring to thought it may help. Some applications of the ZAMO frame are applied in this article as well. Its 97 pages though lol.

Foundations of Black Hole Accretion Disk Theory
Marek A. Abramowicz, P. Chris Fragile
(Submitted on 28 Apr 2011 (v1), last revised 21 Jan 2013 (this version, v3))

This review covers the main aspects of black hole accretion disk theory. We begin with the view that one of the main goals of the theory is to better understand the nature of black holes themselves. In this light we discuss how accretion disks might reveal some of the unique signatures of strong gravity: the event horizon, the innermost stable circular orbit, and the ergosphere. We then review, from a first-principles perspective, the physical processes at play in accretion disks. ...

http://arxiv.org/abs/1104.5499

edit: I found the article a highly useful source of accretion disk dynamics, covers each aspect in it in some nice detail. Also includes the ZAVO metrics as well

 

[WannabeNewton]

I'll have to take a closer look at what the sources are saying regarding Thomas precession in gravitational fields because there seems to be contention surrounding it and a lot of it seems to result solely from calculations.

Ohanian's description for Lense-Thirring precession is very much like the paddle wheel in a fluid vortex analogy.

Well, we should be a little careful here. If you place a paddle wheel in a fluid vortex, there are in general torques applied to different paddles from the fluid velocity field and the wheel starts to rotate. As such it gains an intrinsic spin angular momentum. This is easy to quantify of course because it's simply give by the spin 4-vector $\vec{S}$ (which is by definition the Hodge dual of the spin 2-form) and the net torque on the paddle wheel relative to a given observer is simply $\frac{d \vec{S}}{d\tau}$. Operationally we can measure $\vec{S}$ by placing at the center of the paddle wheel a compass of inertia. Now imagine the paddle wheel is infinitesimally small so that each paddle is described by a single respective world-line. If the paddle wheel is to remain rigid, the world-lines better be integral curves of a time-like Killing field $\vec{\eta} = \vec{\xi}+ \omega \vec{\psi}$. Then the rotation/spin angular momentum $\vec{S}$ of the paddles relative to the compass of inertia at the center of the paddle wheel is exactly what $\vec{\omega} = \vec{\nabla}\times_{\eta} \vec{\eta}$ measures.

But this is obviously not the same thing as the orbital angular momentum $L$ which measures something entirely different and is in general very weakly related to $\vec{\omega}$, unlike $\vec{S}$ which is very strongly related to $\vec{\omega}$ (however as shown in post #161, for static observers $L$ and $\vec{\omega}$ are strongly related).

Did you get a chance to check out the the possible typos in the Rindler paper in post 158 here https://www.physicsforums.com/showthread.php?t=729416&page=9 ?

I'm doing that now. Looking through the calculations should also help shed light on the Thomas precession "issue" mentioned above.

 

[PeterDonis]

I'll have to take a closer look at what the sources are saying regarding Thomas precession in gravitational fields because there seems to be contention surrounding it and a lot of it seems to result solely from calculations.

Some of it may be more an issue of terminology than anything else. Consider the actual formulas for Minkowski, Schwarzschild, and Kerr spacetimes, with each individual term split out (these are precession rates of gyroscopes relative to a static observer at infinity, so I've adjusted the signs appropriately, divided by $\gamma$, and and subtracted out $\omega$ from the formulas in Bill_K's blog post):

$$
\Omega_{Minkowski} = - \left( \gamma - 1 \right) \omega
$$

$$
\Omega_{Schwarzschild} = - \left( \gamma - 1 \right) \omega + \gamma \omega \frac{3M}{r}
$$

$$
\Omega_{Kerr} = - \left( \gamma - 1 \right) \omega + \gamma \omega \frac{3M}{r} \left( 1 - a \omega \right) - \gamma \frac{M a}{r^3} \left( 1 - a \omega \right)^2
$$

As you can see, each successive formula introduces a new term; the standard nomenclature calls the first term (the one that appears in all three) "Thomas precession", the second term (which appears in the last two and has an extra factor in the third) "de Sitter precession" or "geodetic precession", and the third term (which appears only in the last formula) "Lense-Thirring precession" (I've also seen "Schiff precession", I believe that's what the Rindler paper calls it). With the signs as above, positive terms are prograde and negative terms are retrograde; some sources flip the signs.

Mathematically, this is all nice and neat, and invites a nice and neat terminology to match, which I've just given above. Physically, however, there are some issues if we try to get specific with our interpretation of Thomas precession. Thomas precession is standardly interpreted as being due to the non-commutativity of Lorentz boosts. But if that's the case, surely the sign of the precession should depend on the sign of the boost, i.e., on the sign of the proper acceleration. In the Minkowski case, the sign of the proper acceleration is always negative (i.e., radially inward), and the sign of the Thomas precession term in the formulas above is likewise always negative. But in the Schwarzschild and Kerr cases, the sign of the boost depends on $\omega$; it is positive for $\omega = 0$, becomes zero at the value of $\omega$ corresponding to a geodesic orbit, and is negative for larger values of $\omega$. (We'll leave out the other effects that come into play when the radius gets small enough.) Yet the term in the formula for Schwarzschild and Kerr is identical to the Minkowski one*. What gives?

To me, this just means you need to be careful with physical interpretation; it may not match your intuitions, and there may be different ways of trying to resolve any mismatch between the math and your intuitions. (For example, some sources talk about Thomas precession being due to "coordinate boosts" being non-commutative--i.e., the orbits in all three cases above are curved "inward" with respect to the asymptotic Lorentz frame at infinity, and by the "same amount", so of course the Thomas precession term will look the same in all three cases. But as the scare-quotes make clear, this is a hand-waving argument and doesn't really make sense in terms of physical invariants.)

* - Actually this isn't quite true, because of the definition of $\gamma$; as used here, it is the total "time dilation" factor relative to infinity, so in the Schwarzschild and Kerr cases it includes the effect of altitude as well as motion; e.g., in the Schwarzschild case $\gamma = 1 / \sqrt{1 - 2M / r - \omega^2 r^2}$. But this doesn't affect the sign of the precession; it only adjusts its magnitude.

 

[WannabeNewton]

But in the Schwarzschild and Kerr cases, the sign of the boost depends on $\omega$; it is positive for $\omega = 0$, becomes zero at the value of $\omega$ corresponding to a geodesic orbit, and is negative for larger values of $\omega$.

Here's where I think the various ambiguities come from. Ohanian's derivation of the geodetic precession in the weak field limit for example uses a frame fixed to the center of the Earth (ignoring its rotation) and considers a gyroscope in circular free fall orbit around the Earth. Then we apply consecutive Lorentz boosts from the fixed Earth frame to the continuous one-parameter family of local inertial frames of the gyroscope. Here $\omega$ corresponding to a geodesic orbit doesn't have a vanishing boost velocity but rather has a boost velocity corresponding to the tangential velocity due to the centripetal acceleration. A static gyroscope OTOH would have a vanishing boost velocity because it's at rest with respect to the fixed Earth frame. Other sources, such as the ones that claim Thomas precession vanishes for the circular geodesic orbits because the acceleration vanishes, are considering boosts with respect to the local inertial frames themselves. This is where I think the canonical interpretation of Thomas precession breaks down because there is no single fixed local inertial frame but rather a continuous one-parameter family of them so there is no background frame to boost from at each instant of orbit proper time to the instantaneously comoving local inertial frame if we're using the local inertial frames themselves as the standard for what to boost from-if we do conform to the latter then it doesn't make any sense to interpret it as Thomas precession in the same sense as in flat space-time wherein the local inertial frames and fixed static "Earth" frames / asymptotic Lorentz frames all coincide.

 

[yuiop]

(I've also seen "Schiff precession", I believe that's what the Rindler paper calls it).

Rindler seems to use the term "Schiff precession" specifically for precession in a geodesic orbit with no proper acceleration acting on the gyroscopes.

But in the Schwarzschild and Kerr cases, the sign of the boost depends on $\omega$; it is positive for $\omega = 0$, becomes zero at the value of $\omega$ corresponding to a geodesic orbit, and is negative for larger values of $\omega$. (We'll leave out the other effects that come into play when the radius gets small enough.) Yet the term in the formula for Schwarzschild and Kerr is identical to the Minkowski one*. What gives?

Is this not an argument that proper acceleration has nothing to do with Thomas precession. I think WBN said something similar in an earlier post.

Another interpretation is that a gyroscope can somehow sense centrifugal acceleration even when it is canceled out by the gravitational acceleration when in a geodesic orbit. Mathematically the proper acceleration acting on the gyroscope is zero. Is it possible that since no gyroscope is a mathematical point particle, it is sensitive to tiny tidal differences, so that even in a perfect geodesic orbit, extremities of the gyroscope can detect the slight differences between the centrifugal force and the gravitational force that only exactly cancel out at the centre of mass of the object?

To me, this just means you need to be careful with physical interpretation; it may not match your intuitions, and there may be different ways of trying to resolve any mismatch between the math and your intuitions. (For example, some sources talk about Thomas precession being due to "coordinate boosts" being non-commutative--i.e., the orbits in all three cases above are curved "inward" with respect to the asymptotic Lorentz frame at infinity, and by the "same amount", so of course the Thomas precession term will look the same in all three cases. But as the scare-quotes make clear, this is a hand-waving argument and doesn't really make sense in terms of physical invariants.)

Surely, the fact that spacetime is locally Minkowskian in a gravitational field (even if only on an infinitesimal scale) means that Lorentz type boosts are still valid locally even in a gravitational field? Certainly, WBN seemed to indicate that he preferred the non-commutative nature of Lorentz boosts as the explanation for Thomas precession, rather than the acceleration explanation. In fact that was the main topic of the other precession thread.

 

[yuiop]

The retrograde nature of Thomas you already have an intuition for. The geodetic precession is just a spin-orbital coupling so we would expect it to be prograde. ...

Kip Thorne gives a very easy to visualise demonstration of the geodetic precession effect, about a quarter way into this brief video clip.

https://einstein.stanford.edu/MISSION/mission1.html

If the demonstration is correct, it makes it very clear that geodetic precession is prograde, as you say.

 

[WannabeNewton]

Is it possible that since no gyroscope is a mathematical point particle, it is sensitive to tiny tidal differences, so that even in a perfect geodesic orbit, extremities of the gyroscope can detect the slight differences between the centrifugal force and the gravitational force that only exactly cancel out at the centre of mass of the object?

Well the only centrifugal force on the gyroscope would come from its intrinsic spin, which of course we use to define a spin axis for the gyroscope that gets Fermi-transported along a chosen world-line. But the gyroscope is assumed to be very small so the bulging effects will be entirely negligible and we can simply treat the gyroscope as a sphere (recall that the centrifugal force is first order in the radius of the object). We need spherical gyroscopes because it is a spherical shape that allows the gyroscope to be torque-free. If it weren't spherical then it would experience gravitational tidal torques and the usual equations for precession wouldn't hold because those assume the gyroscope is being Fermi-transported along the chosen world-line.

 

[yuiop]

Well the only centrifugal force on the gyroscope would come from its intrinsic spin, which of course we use to define a spin axis for the gyroscope that gets Fermi-transported along a chosen world-line. But the gyroscope is assumed to be very small so the bulging effects will be entirely negligible and we can simply treat the gyroscope as a sphere (recall that the centrifugal force is first order in the radius of the object). We need spherical gyroscopes because it is a spherical shape that allows the gyroscope to be torque-free. If it weren't spherical then it would experience gravitational tidal torques and the usual equations for precession wouldn't hold because those assume the gyroscope is being Fermi-transported along the chosen world-line.

Even a perfectly spherical object in geodesic orbit is subject to tidal forces which is the cause of the Roche limit for orbiting bodies, which causes them to break up in extreme circumstances. The only way to completely eliminate this effect is to have a point particle and I imagine by its very nature, a gyroscope cannot be a point particle.

http://en.wikipedia.org/wiki/Roche_limit

P.S. I am not suggesting that the tidal forces cause a direct torque on the gyroscope. I am just suggesting that somehow the geodesically orbiting gyroscope is aware of the centrifugal forces, in the same way scientists with sensitive enough instruments in a large enough geodesically orbiting lab, could determine they are not moving inertially in flat space, without looking out the window.

 

[WannabeNewton]

Even a perfectly spherical object in geodesic orbit is subject to tidal forces which is the cause of the Roche limit for orbiting bodies, which causes them to break up in extreme circumstances. The only way to completely eliminate this effect is to have a point particle and I imagine by its very nature, a gyroscope cannot be a point particle.

http://en.wikipedia.org/wiki/Roche_limit

Again, that is first order in the radius of the gyroscope. The radius of the gyroscope is assumed to be negligibly small so the effect won't matter. We don't need to completely eliminate it, we just need to make it higher order than the order of the effect we're interested in (the gyroscopic precession) and the assumption of a very small gyroscope does exactly that. Also bear in mind that the entire game of using gyroscopes is just for operational purposes and physical realization. Mathematically there is no need to ever consider a gyroscope-all we need is a spin vector to Fermi-transport and the precession is simply the precession of the spin vector.

 

[PeterDonis]

Is this not an argument that proper acceleration has nothing to do with Thomas precession.

I think it's an argument that the term in the mathematical formulas that is usually called "Thomas precession" can't be explained by proper acceleration, yes. However, I don't think that vindicates the "usual" explanation in terms of non-commutative Lorentz boosts either. See further comments below.

Surely, the fact that spacetime is locally Minkowskian in a gravitational field (even if only on an infinitesimal scale) means that Lorentz type boosts are still valid locally even in a gravitational field?

Yes, definitely; but relative to local inertial frames, the boosts at different events along a geodesic orbit in curved spacetime will "line up" differently than the boosts at different events along a non-geodesic orbit in flat spacetime, even if the "shape" of both orbits relative to infinity is the same. See further comments below.

Certainly, WBN seemed to indicate that he preferred the non-commutative nature of Lorentz boosts as the explanation for Thomas precession, rather than the acceleration explanation.

But the "boosts" in question are not "real" boosts--"real" boosts are always associated with proper acceleration. Put another way, "real" boosts are boosts relative to the local inertial frame at a given event, not relative to some asymptotic global "inertial" frame that isn't really inertial in a curved spacetime. The "boosts" whose non-commutativity is supposed to explain the term in the formulas that is called "Thomas precession", whose sign is always the same, are relative to an asymptotical global "inertial" frame, not relative to any actual local inertial frame; if the boosts were relative to local inertial frames, they would look different in curved spacetime than in flat spacetime, because the local inertial frames are different--the difference in proper acceleration is one manifestation of this. But boosts relative to the asymptotic global "inertial" frame have no physical meaning that I can see; they're just coordinate artifacts. So I don't see how these "boosts" can be used to explain a real, frame-independent physical effect.

(WBN was saying the same thing as the last part--he was just arguing that the "boosts" relative to the asymptotic global "inertial" frame can be used to explain why the term in the formulas that is called "Thomas precession" looks the same in flat spacetime as in curved spacetime. I'm still not sure I buy that because those boosts aren't "real", as I argued above.)

 

[WannabeNewton]

(WBN was saying the same thing as the last part--he was just arguing that the "boosts" relative to the asymptotic global "inertial" frame can be used to explain why the term in the formulas that is called "Thomas precession" looks the same in flat spacetime as in curved spacetime. I'm still not sure I buy that because those boosts aren't "real", as I argued above.)

Actually I'm entirely in agreement with you because the boosts that Ohanian applies in his derivation from the frame fixed to the center of the Earth (which is at rest with respect to the asymptotic Lorentz frame) to an instantaneously comoving local inertial frame aren't really boosts in the strict mathematical sense since in curved space-time boosts only make sense locally. However the derivation in Ohanian was in the weak field limit so to a good approximation we can perform such boosts from the asymptotic Lorentz frame to an instantaneously comoving local inertial frame since we only work to first order in the metric perturbation. In a more general setting it would of course be rather suspect.

 

[PeterDonis]

In a more general setting it would of course be rather suspect.

Yes, and the formulas I wrote down are valid generally, not just in the weak field limit.

 

[WannabeNewton]

http://physics.stackexchange.com/qu...ct-into-thomas-precession-and-spatial-curvatu

 

[WannabeNewton]

Hey guys I have a question that cropped up when reading a paper by Ashtekar on rotation in Kerr space-time. So we know that if we have a time-like vector field $\xi^{\mu}$ and $\xi_{[\gamma}\nabla_{\mu}\xi_{\nu]} = 0$ then we can synchronize the clocks following orbits of $\xi^{\mu}$ such that the resulting simultaneity surfaces are everywhere orthogonal to $\xi^{\mu}$ i.e. we can Einstein synchronize the clocks modulo gravitational time dilation effects and the likes. As far as I know this result applies to any and all time-like vector fields i.e. there are no requirements that it be a Killing field etc.

But this is for clocks of an entire vector field. Say we only cared about synchronizing a specific subset of the clocks in such a manner. For example say we have a single ZAMO ring in Kerr space-time and wish only to synchronize clocks at rest on the ZAMO ring. Denote by $\mathcal{R}$ the submanifold in space-time describing the ZAMO ring and let $\xi^{\mu}|_{\mathcal{R}}$ be its tangent field. Then is there a way to apply the result from above to $\xi^{\mu}|_{\mathcal{R}}$ and from it deduce that clocks at rest on the ZAMO ring are Einstein synchronizable? In other words if $\xi_{[\gamma}\nabla_{\mu}\xi_{\nu]}|_{\mathcal{R}} = 0$ can I say the clocks on the ZAMO ring are Einstein synchronizable in the sense defined above?

The reason I ask is, as we've talked about earlier, there is more than one way to extend $\xi^{\mu}|_{\mathcal{R}}$ to a neighborhood of $\mathcal{R}$ before computing $\xi_{[\gamma}\nabla_{\mu}\xi_{\nu]}|_{\mathcal{R}}$. We can extend it to $\xi^{\mu} = t^{\mu} + \omega \psi^{\mu}$, where $t^{\mu},\psi^{\mu}$ are the time-like and rotational Killing fields and $\omega := \omega(r,\theta)$ or we can extend it to $\tilde{\xi}^{\mu} = t^{\mu} + \omega_0 \psi^{\mu}$ where $\omega_0 := \omega(r_0,\theta_0)$ throughout space-time. As we've seen, $\xi_{[\gamma}\nabla_{\mu}\xi_{\nu]} = 0$ but $\tilde{\xi}_{[\gamma}\nabla_{\mu}\tilde{\xi}_{\nu]}\neq 0$ so if we applied the result aforementioned then one extension would yield synchronizable clocks on the ZAMO ring whereas the other extension would yield non-synchronizable clocks on the same ZAMO ring. But we've changed nothing about the kinematics of the ZAMO ring itself-whether or not the clocks on it are synchronizable should depend only on the behavior of $\xi_{[\gamma}\nabla_{\mu}\xi_{\nu]}|_{\mathcal{R}}$ and not on how we extend it which has nothing to do with the ZAMO ring itself. So would it be fair to say that the above result cannot be so easily restricted to subsets of a given space-time filling family of clocks?

 

[PeterDonis]

As far as I know this result applies to any and all time-like vector fields i.e. there are no requirements that it be a Killing field etc.

I think this is technically correct, but it has some weird physical implications. For example, the congruence of "comoving" observers in FRW spacetime meets the requirements, since it is everywhere timelike and irrotational; and the conclusion appears to hold since surfaces of constant FRW coordinate time are everywhere orthogonal to the congruence. But if you think about how you would "Einstein synchronize" comoving clocks, by sending round-trip light signals between them, while this would indeed give you the surfaces of constant FRW coordinate time as your surfaces of simultaneity, the time between successive round-trip light signals would not be constant; in the usual case of an expanding FRW spacetime, the round-trip light travel time between two comoving observers would be increasing. "Einstein synchronization" seems to be a weird term to describe this, since that term is usually taken to imply a constant round-trip light travel time. In other words, "Einstein synchronization" is usually taken to imply a rigid congruence, but the "comoving" congruence in FRW spacetime is of course not rigid, since it has nonzero expansion.

In other words if $\xi_{[\gamma}\nabla_{\mu}\xi_{\nu]}|_{\mathcal{R}} = 0$ can I say the clocks on the ZAMO ring are Einstein synchronizable in the sense defined above?

I'm not sure the derivatives you need to take will be well-defined if you restrict to a single ZAMO ring. The physical interpretation of the vorticity requires Lie transported vectors pointing to neighboring members of the congruence; but if you restrict to a single ZAMO ring, there are no "neighboring" members in any direction off the ring, so how can you take the appropriate derivatives in those directions?

If your response to the above is that we just restrict all derivatives to the two-dimensional subspace of the chosen ZAMO ring, consider that, in order to Einstein synchronize two clocks on the same ZAMO ring, they have to exchange light signals, and those light signals will not be restricted to that ZAMO ring (unless it happens to be at the same radius as a photon orbit). So any physical interpretation of the theorem in question will implicitly have to rely on some extension of the congruence off the chosen ZAMO ring.

whether or not the clocks on it are synchronizable should depend only on the behavior of $\xi_{[\gamma}\nabla_{\mu}\xi_{\nu]}|_{\mathcal{R}}$ and not on how we extend it which has nothing to do with the ZAMO ring itself.

I'm not sure this is true; see above.

 

[yuiop]

I'm not sure the derivatives you need to take will be well-defined if you restrict to a single ZAMO ring. The physical interpretation of the vorticity requires Lie transported vectors pointing to neighboring members of the congruence; but if you restrict to a single ZAMO ring, there are no "neighboring" members in any direction off the ring, so how can you take the appropriate derivatives in those directions?

I have tried to find a definition of Lie transported vectors on the internet without any luck. (Any help on that would be appreciated). I guess a lot depends on how the congruence is defined. If we have a congruence of members with equal orbital angular velocity, then we have a rigid congruence and members of such a congruence would be at rest with orthonormal basis vectors such that a vector at rest in this congruence that is initially pointing at the centre of the orbit will remain pointing at the centre of the orbit. Rindler is clearly using a rigid congruence to define vorticity and since his equations agree with other sources, it would would appear all definitions of vorticity are relative to a rigid congruence or orthonormal basis vectors. If the formal definition of vorticity is relative to Lie transported vectors and if the formal definition of Lie transported vectors is relative to a congruence of members with equal angular momentum, then things get very messy in the Kerr metric due to sheer. For what its worth I have calculated the averaged rotation of the non rigid equal momentum congruence in the Kerr metric using regular Newtonian fluid dynamics (i.e. the paddle wheel) to be:

$\frac{-4ma(r^2-ma^2/r)}{r^3(r^2+a^2+2ma^2/r)^2}$

This turns out to be a factor of approximately 4/3 larger than the ZAMO precession rate of:

$\frac{-ma(3r^2+a^2)}{r^3(r^2+a^2+2ma^2/r)}$

and approximately 4 times larger than the precession rate of gyroscope held by a static observer in the Kerr metric of:

$\frac{-ma}{r^3(1-2m/r)}$

for large r. I can show how I obtained this result if you are interested. Although this Newtonian fluid vorticity is not exactly equal to the GR precession rate, there does appear to be a close connection.

If your response to the above is that we just restrict all derivatives to the two-dimensional subspace of the chosen ZAMO ring, consider that, in order to Einstein synchronize two clocks on the same ZAMO ring, they have to exchange light signals, and those light signals will not be restricted to that ZAMO ring (unless it happens to be at the same radius as a photon orbit). So any physical interpretation of the theorem in question will implicitly have to rely on some extension of the congruence off the chosen ZAMO ring.

The paper referred to by WBN uses "a hollow toroidal tube of glass with perfectly reflecting internal walls" to transit the light signals and so restricts the light path to the ring. Could we not use such a reflecting tube to transmit the synchronisation signals and restrict the analysis to the ring only?

 

[WannabeNewton]

"Einstein synchronization" seems to be a weird term to describe this, since that term is usually taken to imply a constant round-trip light travel time. In other words, "Einstein synchronization" is usually taken to imply a rigid congruence, but the "comoving" congruence in FRW spacetime is of course not rigid, since it has nonzero expansion.

I certainly agree with you there.

I'm not sure the derivatives you need to take will be well-defined if you restrict to a single ZAMO ring. The physical interpretation of the vorticity requires Lie transported vectors pointing to neighboring members of the congruence; but if you restrict to a single ZAMO ring, there are no "neighboring" members in any direction off the ring, so how can you take the appropriate derivatives in those directions?

Right which is why I said we have to extend the vector field to a neighborhood of $\mathcal{R}$. But the problem for me is there is no unique way to perform such an extension. One extension gives us a vector field with vanishing vorticity (the ZAMO congruence) whereas the other gives us a vector field with non-vanishing vorticity (a Killing congruence which agrees with the ZAMO ring when restricted to $\mathcal{R}$). So one extension would give us a synchronizable vector field whereas the other wouldn't even though both yield the same exact ZAMO ring and vector field when restricted to $\mathcal{R}$.

The problem of course is the vanishing vorticity condition for synchronization requires as you said derivatives in all directions in space-time. This is no problem if we're talking about a vector field filling all of space-time but if we're talking about only the tangent field to $\mathcal{R}$ then it isn't enough to only have the derivatives along $\mathcal{R}$ we also need the derivatives perpendicular to $\mathcal{R}$ i.e. the radial and polar derivatives. This would require us to extend the tangent field off of $\mathcal{R}$ but there is no unique way to do so as stated so this is why I was unsure as to whether the vanishing vorticity condition for synchronization could actually apply to 2-dimensional submanifolds like $\mathcal{R}$ or could only apply to vector fields filling all of space-time.

Is my confusion apparent?

If your response to the above is that we just restrict all derivatives to the two-dimensional subspace of the chosen ZAMO ring, consider that, in order to Einstein synchronize two clocks on the same ZAMO ring, they have to exchange light signals, and those light signals will not be restricted to that ZAMO ring (unless it happens to be at the same radius as a photon orbit). So any physical interpretation of the theorem in question will implicitly have to rely on some extension of the congruence off the chosen ZAMO ring.

I was thinking, just like in the case of the rotating disk in flat space-time, we place concave mirrors along the circumference of the ring and exchange light signals along the ring using the mirrors. Granted the light signals will follow null curves that aren't geodesics but it still allows us to exchange signals between points of the ring alone.

 

[WannabeNewton]

I have tried to find a definition of Lie transported vectors on the internet without any luck. (Any help on that would be appreciated).

You'll find it in most standard GR texts and every differential topology text. Take a vector field $\xi^{\mu}$ and another vector field $\eta^{\mu}$. Then $\eta^{\mu}$ is Lie transported along $\xi^{\mu}$ if $\mathcal{L}_{\xi}\eta^{\mu} := \xi^{\nu}\partial_{\nu}\eta^{\mu} - \eta^{\nu}\partial_{\nu}\xi^{\mu} = 0$. This is a completely general definition with no reference to any frames (orthonormal basis vectors). If we are using a torsion-free connection then we can replace $\partial_{\mu}$ with $\nabla_{\mu}$.

Rindler is clearly using a rigid congruence to define vorticity and since his equations agree with other sources, it would would appear all definitions of vorticity are relative to a rigid congruence or orthonormal basis vectors.

Well vorticity is defined for any congruence without reference to any kind of frame and is simply $\omega^{\mu} = \epsilon^{\mu\nu\alpha\beta}\xi_{\nu}\partial_{\alpha}\xi_{\beta}$.

But if you want to interpret vorticity in terms of rotation of Lie transported orthonormal basis vectors relative to local gyroscopes then you need a Killing congruence, or possibly just a rigid congruence although I have yet to see a proof that goes beyond Killing congruences.

If the formal definition of vorticity is relative to Lie transported vectors and if the formal definition of Lie transported vectors is relative to a congruence of members with equal angular momentum, then things get very messy in the Kerr metric due to sheer.

Thankfully neither of those are true :)

 

[PeterDonis]

there is no unique way to perform such an extension. One extension gives us a vector field with vanishing vorticity (the ZAMO congruence) whereas the other gives us a vector field with non-vanishing vorticity (a Killing congruence which agrees with the ZAMO ring when restricted to $\mathcal{R}$). So one extension would give us a synchronizable vector field whereas the other wouldn't even though both yield the same exact ZAMO ring and vector field when restricted to $\mathcal{R}$.

Yes, but that doesn't make them the same vector field or the same congruence. You are talking about two different congruences--the ZAMO congruence and the constant-angular-velocity Killing congruence--that just happen to have the same restriction to a particular submanifold ($\mathcal{R}$). So yes, there's no unique "vorticity" for the restriction to $\mathcal{R}$, because that restriction doesn't define a unique congruence--more precisely, it doesn't define "enough" of one to have a well-defined, unique vorticity.

this is why I was unsure as to whether the vanishing vorticity condition for synchronization could actually apply to 2-dimensional submanifolds like $\mathcal{R}$ or could only apply to vector fields filling all of space-time.

I think the actual range of application is somwhere in between. For example, consider the 3-dimensional submanifold of Kerr spacetime that we call the "equatorial plane". The restriction of the ZAMO congruence to this submanifold has a well-defined (vanishing) vorticity, and the Killing (i.e., constant angular velocity) congruence on this submanifold also has a well-defined (non-vanishing) vorticity. But this is still not all of spacetime; it's a 3-dimensional submanifold.

I think it's worth noting that the Newtonian case works the same way. You can't define vorticity for a Newtonian "fluid" that only moves in one spatial dimension (for example, flow in a really thin pipe modeled as a one-dimensional flow); you have to at least have two spatial dimensions involved (for example, flow restricted to a plane).

 

[yuiop]

In the Ashtekar paper linked by WBN, two examples for the Sagnac shift are given, which when restricted to the equatorial plane can be expressed as:

$\Delta \tau = 16\pi\frac{ ma}{r\sqrt{1-2m/r}}$ for a stationary ring in the Kerr case and

$\Delta \tau = 4\pi\frac{ \omega r^2}{\sqrt{1-\omega^2r^2}}$ for a rotating ring in the Minkowski case.

If the precession angular velocity measured at infinity relative to the orthonormal basis vectors is denoted by $\Omega$ then the two equations above can then be expressed as:

$\Delta \tau = 16\pi r^2 \Omega$ for a stationary ring in the Kerr case and

$\Delta \tau = 4\pi r^2 \Omega$ for a rotating ring in the Minkowski case.

I find this relationship interesting. I wonder if someone could find an expression for the equatorial Kerr case for arbitrary orbital angular velocity? I feel it will be enlightening.

 

[WannabeNewton]

So yes, there's no unique "vorticity" for the restriction to $\mathcal{R}$, because that restriction doesn't define a unique congruence--more precisely, it doesn't define "enough" of one to have a well-defined, unique vorticity.

Thanks Peter. The reason I asked is regarding the relationship between the Sagnac effect and clock synchronization relative to a time-like congruence, in the sense of local Einstein synchronization propagated throughout the congruence. In the Ashtekar paper, a stationary space-time is considered with time-like Killing field $t^{\mu}$ and a tube made of perfectly reflecting internal mirrors is considered such that each point of the tube follows an orbit of $t^{\mu}$-the paper terms this a 'Sagnac tube'. Clearly such a Sagnac tube is at rest in the gravitational field. Then the paper derives the following relationship between the Sagnac shift $\Delta \tau$ of prograde and retrograde light signals emitted from a half-silvered mirror placed somewhere inside the tube as measured by a clock comoving with the mirror and the twist $\omega^{\mu} = \epsilon^{\mu\nu\alpha\beta}t_{\nu}\nabla_{\alpha}t_{\beta}$ of the time-like Killing field which also happens to be the tangent field to the Sagnac tube:

\Delta \tau = (\lambda_M)^{1/2}\int_{\Sigma} \lambda^{-3/2}\omega^{i}\epsilon_{ijk}dS^{jk}

where $\lambda = -t^{\mu}t_{\mu}$, $\lambda_M$ is this field restricted to the world-line $M$ of the mirror, and $\Sigma$ is the region bounded by a closed curve $C$ on the 2-manifold representing the tube.

Therefore for Sagnac tubes at rest in the gravitational field of the stationary space-time, the Sagnac shift vanishes if the twist (vorticity) vanishes. At the same time, clocks laid out along the circumference of the tube will be synchronizable in the above sense if the twist vanishes and in fact if the twist doesn't vanish, the time discontinuity accrued by attempting local Einstein synchronization around the tube will be exactly given by the Sagnac shift. Examples are clocks laid out along Sagnac tubes at rest in Kerr space-time and along peripheries of rotating disks in flat space-time.

Consider Kerr space-time again but a Sagnac tube whose points follow orbits of the Killing field $\tilde{\xi}^{\mu} = t^{\mu} + \omega_0 \psi^{\mu}$ with $\omega_0$ being a fixed/constant ZAMO angular velocity. Then in general $\tilde{\omega}^{\mu} = \epsilon^{\mu\nu\alpha\beta}\tilde{\xi}_{\nu}\nabla_{\alpha}\tilde{\xi}_{\beta}\neq 0$ but on the tube itself we have $L = \psi_{\mu}\tilde{\xi}^{\mu} = 0$ which, according to Proposition 3.2.2. in Malament's text, means there is no Sagnac effect for this tube. Therefore if the Sagnac tube is not at rest in the gravitational field but rather has some angular velocity then we can choose a tangent field for the tube, such as the Killing field above, for which the twist doesn't vanish but the Sagnac shift still does. Since the standard clocks following orbits of $\tilde{\xi}^{\mu}$ cannot be synchronized with one another in the usual sense if $\tilde{\omega}^{\mu} \neq 0$, does this mean there is no general relationship between clock synchrinization (or lack thereof) and the Sagnac shift if the Sagnac tube has an angular velocity relative to infinity and follows the Killing field $\tilde{\xi}^{\mu}$?

 

[PeterDonis]

Consider Kerr space-time again but a Sagnac tube whose points follow orbits of the Killing field $\tilde{\xi}^{\mu} = t^{\mu} + \omega_0 \psi^{\mu}$ with $\omega_0$ being a fixed/constant ZAMO angular velocity.

I think it's worth noting here that the *reason* the Sagnac tube has to follow orbits of the Killing congruence, not the (varying angular velocity) ZAMO congruence, is that the congruence describing the Sagnac tube must be rigid. Otherwise the tube won't work properly. So it's really a physical requirement that's being modeled by choosing a Killing congruence, which is what drives everything else.

Since the standard clocks following orbits of $\tilde{\xi}^{\mu}$ cannot be synchronized with one another in the usual sense if $\tilde{\omega}^{\mu} \neq 0$, does this mean there is no general relationship between clock synchrinization (or lack thereof) and the Sagnac shift if the Sagnac tube has an angular velocity relative to infinity and follows the Killing field $\tilde{\xi}^{\mu}$?

It looks that way to me, yes.

 

[WannabeNewton]

Peter it seems I spoke too soon. Take a Sagnac tube $\mathcal{R}$ in Kerr space-time with the tangent field $\xi^{\mu}_{\mathcal{R}} = t^{\mu} + \omega|_{\mathcal{R}}\psi^{\mu}$ where $\omega|_{\mathcal{R}} = -\frac{g_{t\phi}}{g_{\phi\phi}}$. Then two neighboring clocks on the tube will be (locally Einstein) synchronized if $\xi^{\mu}_{\mathcal{R}}dx_{\mu} = 0$ where $dx^{\mu}$ is the space-time displacement between the two (locally Einstein) simultaneous events on the world-lines of the clocks. Expanding this out we see that $dt \propto g_{t\phi} + \omega|_{\mathcal{R}}g_{\phi\phi} = 0$ and hence $\oint_{\gamma} dt = 0$ for any closed simultaneity curve $\gamma$ on $\mathcal{R}$. At the same time we know as well that the Sagnac shift vanishes for this tube.

This is entirely independent of how we extend $\xi_{\mathcal{R}}^{\mu}$ to all of space-time i.e. it doesn't matter whether we use the tangent field of the zero angular momentum congruence or that of the Killing congruence. So again we have clock synchronization and vanishing Sagnac shift occurring simultaneously. Also it would seem from this that, as an upshot, the condition $\xi_{[\gamma}\nabla_{\mu}\xi_{\nu]} = 0$ for clock synchronization really doesn't apply to single rings or Sagnac tubes due to the issue already discussed regarding the non-uniqueness of the extension $\xi^{\mu}$ of $\xi_{\mathcal{R}}^{\mu}$ to all of space-time. So I guess what we could say is the twist of $\xi^{\mu}$ is in general unrelated to the Sagnac shift for, and clock synchronization along, Sagnac tubes that have non-vanishing angular velocities relative to infinity (in this case the frame-dragging angular velocity) simply because there is no unique such twist we could even assign to the Sagnac tube when all we know is $\xi^{\mu}_{\mathcal{R}}$. But would it be fair to conclude that there is indeed a relationship between the Sagnac shift and clock synchronization or was this just a coincidence?

 

[PeterDonis]

Take a Sagnac tube $\mathcal{R}$ in Kerr space-time with the tangent field $\xi^{\mu}_{\mathcal{R}} = t^{\mu} + \omega|_{\mathcal{R}}\psi^{\mu}$ where $\omega|_{\mathcal{R}} = -\frac{g_{t\phi}}{g_{\phi\phi}}$.

This tube is restricted to $\mathcal{R}$, which means it's restricted to a 2-dimensional submanifold spanned by the $t, \phi$ coordinates, at constant $r, \theta$. Malament would call this the "striated orbit cylinder" at $r, \theta$. So "neighboring clocks on the tube" are just nearby striations on the cylinder, i.e., nearby worldlines in the 2-dimensional submanifold. But we've already seen that you can't define vorticity in a 2-dimensional submanifold anyway; all you need to synchronize clocks in this submanifold is for the worldlines describing the clocks to be orthogonal to some set of spacelike curves, which of course they are, as you show.

This is entirely independent of how we extend $\xi_{\mathcal{R}}^{\mu}$ to all of space-time

But that's only because we've restricted "neighboring clocks" to mean "neighboring in the $\phi$ direction" only. As soon as we try to consider "neighboring" clocks in any other spatial direction, we have to face the question of how to extend the congruence, and different answers to that question give different outcomes.

So again we have clock synchronization and vanishing Sagnac shift occurring simultaneously.

But only when we restrict to a 2-dimensional submanifold only. In other words, if we want this relationship between vanishing Sagnac shift and clock synchronization to hold, we have to restrict consideration to just the 2-dimensional submanifold that describes the Sagnac ring. We can't look at *any* clocks off the ring. That seems like a very strong restriction to me.

it would seem from this that, as an upshot, the condition $\xi_{[\gamma}\nabla_{\mu}\xi_{\nu]} = 0$ for clock synchronization really doesn't apply to single rings or Sagnac tubes due to the issue already discussed regarding the non-uniqueness of the extension $\xi^{\mu}$ of $\xi_{\mathcal{R}}^{\mu}$ to all of space-time.

Yes.

would it be fair to conclude that there is indeed a relationship between the Sagnac shift and clock synchronization or was this just a coincidence?

It's not a coincidence, but it is a restricted definition of "clock synchronization". See above.

 

[yuiop]

...I wonder if someone could find an expression for the equatorial Kerr case for arbitrary orbital angular velocity? I feel it will be enlightening.

I think I have now figured out the Sagnac delay for arbitrary orbital angular velocity $\omega$ in the equatorial plane of the Kerr metric, using my own brute force method. The result is:

$\Delta \tau = \left(\frac{ 2 \pi r}{S_P-\omega r}-\frac{2\pi r}{S_R+\omega r}\right) \gamma^{-1}$

where $S_P$ and $S_R$ are the prograde(+) and retrograde(-) tangential coordinate speeds of light given by

$\frac{r \sqrt{a^2 +r^2-2mr} \pm 2ma}{r^2+a^2+2ma^2/r}$.

$\gamma= 1/\sqrt{1-\omega^2(a^2+r^2)-(2m/r)(1-a\omega)^2}$ is the time dilation factor for an observer at rest with the rotating Sagnac ring.

Unfortunately the equation does not simplify to anything pretty.
When a=0 and m=0, the equation simplifies to the Minkowski case:

$\Delta \tau = \frac{ 4\pi r^2\omega}{\sqrt{1-\omega^2r^2}}$

When a=0, the equation reduces to the Schwartzschild case:

$\Delta \tau = \frac{4\pi r^2 \omega}{\sqrt{1-2m/r-\omega^2 r^2}}$

For both the above metrics there is a simple relationship between the Sagnac delay and the gyroscope precession rate that is independent of $\omega$.

For the Kerr case, an angular velocity equal to the ZAMO velocity yields a zero Sagac delay as it should.

For arbitrary $\omega$ there is no simple relationship between Sagnac delay and gyroscope precession rate.

When $\omega=0$ the Sagnac delay is:

$\Delta \tau = \frac{8\pi ma}{r\sqrt{1-2m/r}}$

Unfortunately this last result is half that obtained by the Ashtekar paper. My equation passes all the other sanity checks, so I am not sure of the reason for the discrepancy?

 

[WannabeNewton]

yuiop based on the papers I've read, your result for the $\omega = 0$ case is correct, although most sources have the opposite sign which is almost certainly just due to you subtracting retrograde from prograde instead of the opposite so that isn't a problem. Maybe the discrepancy is in Ashtekar's definition of $A_0$ which he never explicitly writes down.

See for example equation (17) in this paper: http://arxiv.org/pdf/gr-qc/0510047.pdf

 

[yuiop]

See for example equation (17) in this paper: http://arxiv.org/pdf/gr-qc/0510047.pdf

I take it back. Your linked paper shows there is a reasonable simplification of the Sagnac delay equation in the Kerr metric, which in the notation I used earlier is

\Delta \tau = 4 \pi\left(\omega(r^2+a^2+2ma^2/r)-2ma/r\right)\gamma

 

[WannabeNewton]

Peter, while looking for more papers on inertial forces in rotating frames in curved space-time I happened upon a paper that more or less settles (in our favor) our previous discussion regarding vorticity being defined as rotation of connecting vectors relative to local gyroscopes (Fermi-transported frames). Take a look at section 3.1 of the following paper, and eq. (45) in particular: http://arxiv.org/pdf/1207.0465.pdf

In the paper's notation, $\omega_{\hat{i}\hat{j}}$ is the rotation of the frame of an observer following an orbit of a particular congruence expressed relative to a chose frame field of the congruence and $\Omega_{\hat{i}\hat{j}}$ is the vorticity of the congruence also expressed relative to the chosen frame field. The other quantities are self-explanatory. Consider now the ZAMO congruence in Kerr space-time; choose the rest frame of each ZAMO observer such that $\omega_{\hat{i}\hat{j}} = \Omega_{\hat{i}\hat{j}}$ i.e. lock the rotation of the axes of the frame to the local circulation due to the vorticity of the congruence. We know the vorticity of the congruence vanishes, that is $\Omega_{\hat{i}\hat{j}} = 0$, so this would be a non-rotating frame in the sense that it agrees with the local Fermi-transported frames.

However, as eq. (40) makes clear, the spatial projection $Y^{\hat{i}}$ of the connecting vectors between neighboring ZAMO observers does not have vanishing angular velocity relative to these rest frames precisely because we have non-vanishing shear, $\sigma_{\hat{i}\hat{j}} \neq 0$. The connecting vectors do in fact rotate in these frames even though the frames themselves have non-rotating spatial axes by definition as they are the frames adapted to the vanishing vorticity of the congruence. Note that in the vanishing vorticity adapted frame, $\frac{d}{dt}Y^{\hat{i}} = 0$ if and only if $\theta = \sigma_{\hat{i}\hat{j}} =0$ i.e. we must have a rigid congruence (although not necessarily a Killing congruence).

In the MTW exercise and previous calculations in this thread, the natural rest frames of the ZAMOs were taken to be the basis vectors adapted to the stationary and axial symmetries of Kerr space-time. As we've seen, these frames do rotate relative to local gyroscopes so they are not the frames adapted to the vanishing vorticity of the ZAMO congruence but rather they rotate relative to the vanishing vorticity adapted frame. This is not surprising of course because the spatial axes of the natural rest frame of a given ZAMO are rigidly locked onto the (non-ZAMO) neighboring observers following orbits of the time-like Killing field $\eta^{\mu} = \xi^{\mu} + \omega_0 \psi^{\mu}$ and since $\eta_{[\gamma}\nabla_{\mu}\eta_{\nu]} \neq 0$ the natural frame would have to rotate relative to the vanishing vorticity adapted frame.

 

[PeterDonis]

The connecting vectors do in fact rotate in these frames even though the frames themselves have non-rotating spatial axes by definition as they are the frames adapted to the vanishing vorticity of the congruence.

Yes, I think this is true, but the interesting question to me is, *how* do the connecting vectors rotate relative to these frames? The key complication that I see here, due to the nonzero shear, is that tangential connecting vectors (i.e., those that, at some instant of a given ZAMO's proper time, point at neighboring ZAMOs that are at the same $r$ but slightly different $\phi$) will rotate *differently*, relative to the Fermi-Walker transported vectors, from the radial connecting vectors (those that, at some instant, point at neighboring ZAMOs at the same $\phi$ but slightly different $r$). Working out, by computation, exactly how they differ has been on my list of things to do in my copious free time for a while now.

 

[WannabeNewton]

You know I've been meaning to ask something. Sometime ago I started a similar thread on the topic of the ZAMO observers in Kerr space-time (perhaps you remember it) and the terminology "locally non-rotating observer" as applied to the ZAMOs confused the living hell out of me. Wald for example uses this terminology when characterizing the ZAMOs (c.f. exercise 7.3) and so does MTW (c.f. exercise 33.3).

But why does this terminology even exist for the ZAMOs? This terminology is usually applied with reference to the "natural" rest frames of the ZAMOs i.e. those frames we obtain by fixing the tetrads to the background time-like and axial symmetries. But as we know these frames do rotate relative to local gyroscopes-the vanishing vorticity of the ZAMOs is not enough to guarantee that the "natural" rest frames of the ZAMOs are non-rotating because the ZAMOs altogether do not follow orbits of a time-like Killing field; each ZAMO alone does follow an orbit of a time-like Killing field but the neighboring observers of this Killing field are not ZAMOs hence the Killing field has non-vanishing vorticity and as we've seen this leads to gyroscopic precession in the "natural" rest frame of a given ZAMO indicating that this frame does in fact rotate as determined by a local compass of inertia.

On the other hand if the terminology is used with reference to Fermi-Walker transported frames attached to ZAMOs (which are by definition non-rotating) then the terminology seems pointless when used specifically for ZAMOs because we can attach Fermi-Walker frames to any and all observers in arbitrary space-times.

 

[PeterDonis]

why does this terminology even exist for the ZAMOs?

I think it's because the term "non-rotating" can have different meanings. One meaning is simply "having zero angular momentum", which obviously applies to a ZAMO. Of course, just making that observation doesn't help with making sense of the other issues involved.

This terminology is usually applied with reference to the "natural" rest frames of the ZAMOs

Is it? I don't have references handy right now, but from what I remember of them, they don't explicitly say this. They simply say that the ZAMO congruence has zero vorticity; but the physical interpretation of zero vorticity for a non-rigid congruence is more complicated than it is for a rigid one. That's what makes this issue difficult to resolve.

the vanishing vorticity of the ZAMOs is not enough to guarantee that the "natural" rest frames of the ZAMOs are non-rotating because the ZAMOs altogether do not follow orbits of a time-like Killing field

I would say it's because the ZAMO congruence is not rigid, as above.

 

[yuiop]

... the interesting question to me is, *how* do the connecting vectors rotate relative to these frames? The key complication that I see here, due to the nonzero shear, is that tangential connecting vectors (i.e., those that, at some instant of a given ZAMO's proper time, point at neighboring ZAMOs that are at the same $r$ but slightly different $\phi$) will rotate *differently*, relative to the Fermi-Walker transported vectors, from the radial connecting vectors (those that, at some instant, point at neighboring ZAMOs at the same $\phi$ but slightly different $r$). Working out, by computation, exactly how they differ has been on my list of things to do in my copious free time for a while now.

This is my attempt to work out the averaged angular velocity of the ZAMO congruence (using the paddle wheel metaphor), to see how it relates to the gyroscope precession. Referring to the diagram below

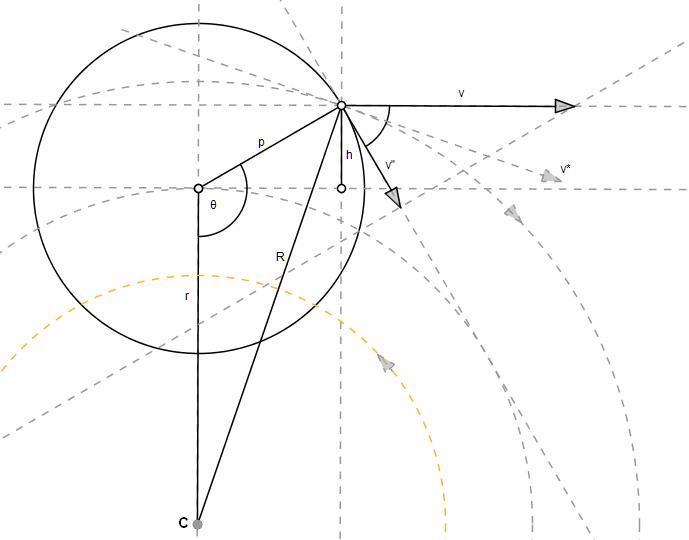
the solid circle represents the paddle wheel with a radius of p and with its centre a distance r from the centre of the Kerr black hole. In the illustration, r is only about twice as big as p, to exaggerate the approximations I make, but normally r would be much greater than the radius of the paddle wheel which can be considered to be infinitesimal. Here I am considering the point of view of a rigid frame co-moving with a ZAMO at radius r, such that faster moving ZAMOs lower down are moving to the left and slower moving ZAMOs higher up are moving to the right. The first part of the calculation is to find the velocity of a given ZAMO at an arbitrary point on the perimeter of the paddle wheel. The distance of this ZAMO from the gravitational centre (C) is R and for the calculation I am using the approximation, R=(r+h). From simple trigonometry $h=-p \cos(\theta)$ so

$R=r -p \cos(\theta)$.

This value of R can be substituted into the ZAMO angular velocity:

$\frac{2ma}{(R^3+a^2R+2ma^2)}$

Multiplying the above by R gives the horizontal velocity (v) of the ZAMO at that radius. This is an approximation because the actual velocity tangential to r is (v*) as shown in the diagram, but the error is small for p<<R. The velocity of the ZAMO frame at altitude R is then subtracted to give the velocities as seen in the rigid frame co-moving with the representative ZAMO. The component of this velocity that is tangential to the paddle wheel perimeter (v') then has to be found and to a reasonable approximation this is $v' = -cos(\theta)*v$.

$v' =-\cos(\theta)\left(\frac{2maR}{(R^3+a^2*R+2ma^2)}-\frac{2maR}{(r^3+a^2r+2ma^2)}\right)$

This is the velocity component tangent to the paddles of the wheel at a given point on the perimeter of the wheel. This value is integrated all the way around the perimeter from $\theta=0$ to $\theta=2\pi$ to sum all the velocities and divided by $2\pi$ to obtain an averaged tangential velocity and further divided by p to obtain the angular velocity of the paddle wheel. Finally the limit is taken as the radius (p) of the paddle wheel goes to zero, because I am looking for the angular velocity of an infinitesimal paddle wheel:

$\Omega_p = \lim_{p \to 0} \left(\frac{1}{2 \pi p} \left( \int_0^{2 \pi} -cos(\theta)\left(\frac{(r-p \cos(\theta))2ma}{(r-p\cos(\theta))^3+a^2(r-p\cos(\theta))+2ma^2}-\frac{(r-p\cos(\theta))2ma}{r^3+a^2r+2ma^2}\right) d\theta \right)\right)$

and the final result is:

$\Omega_p = \frac {-mar (3r^2+a^2)}{(r^3+a^2r+2ma^2)^2}$

The known angular velocity of the gyroscopes in the ZAMO frame is:

$\Omega = \frac {-ma (3r^2+a^2)}{(r^3+a^2r+2ma^2)}$

Dividing $\Omega_p$ by $\Omega$ and plotting the result using $a=0.9$ and $m=c=1$ from r=0 to r=100 gives:

The red curve is the ratio of the paddle wheel angular velocity, relative to the ZAMO gyroscope precession angular velocity and is close to unity all the way down to near the Kerr ergosphere. This is a good match considering the simplifications I had to make. (The green curve is just the time dilation factor of the representative ZAMO for comparison purposes.)

The exact value of R is

$R= \sqrt{r^2+p^2-2pr \cos(\theta)}$

using the solution for a triangle with 2 known side lengths and a known included angle.

The exact value for the tangential velocity v' is

$v' = v*\frac{p-r \cos(\theta)}{\sqrt{r^2+p^2-2 r p \cos(\theta)}}$.

Unfortunately, the hardware and mathematical software I have available is not able to obtain a closed form solution for the integration step when I use the more complicated exact values. An exact solution also requires consideration of how coordinate velocities transform to local velocities and this is not straight forward in the Kerr metric. Nevertheless, this simplified result hints that the rest frame of the un-torqued gyroscopes is simply the averaged angular velocity of the local ZAMO congruence in an infinitesimal region.

P.S. If we equate the precession of the gyroscopes with the 'averaged' rest frame of the local ZAMO congruence, there is a potential complication due to the non rigidity of the congruence. If we had an actual paddle wheel in a fluid flow, the wheel automatically averages the flow, because parts of the wheel immersed in slow flowing fluid are sped up by parts of the wheel immersed in faster flowing fluid (and vice versa) because paddles on the perimeter of the wheel are rigidly connected to each other and the the wheel is forced to rotate a single common angular velocity. On the other hand, gyroscopes cannot be forced to assume a common angular velocity by a similar averaging mechanism, because there will then be a real torque on the slower gyroscopes, causing a torque reaction on the spin axis of the slower gyroscopes so that their spin axis does not remain orthogonal to the equatorial plane. I think this relates to the apparent *anisotropic* rotation of the gyroscopes that Peter is mulling over in the quote at the top of this post, which is at odds with the fact that Fermi transported vectors remain orthogonal to each other. Something does not seem quite right here.

 

[WannabeNewton]

Hey guys, sorry to drag this thread back into the light but I was rereading the "Sagnac Effect in General Relativity" paper by Ashtekar and Magnon (which I think you both have copies of at this point) and I got confused by a technical detail.

To start with, the authors take a space-time $(\mathcal{M},g_{ab})$ and consider a Sagnac tube $(\mu, h_{ab})$ in this space-time such that $\mu$ admits a time-like Killing field $t^{a}$ to which it is tangent. Note that the tangent field $t^{a}$ is only required to be a Killing field on $\mu$ i.e. $\tilde{\nabla}_{(a}t_{b)} = 0$ where $\tilde{\nabla}$ is the derivative operator on $\mu$ associated with its metric $h_{ab}$; hence $t^{a}$ need not necessarily be a Killing field on $\mathcal{M}$ itself. This means in particular that if we are in Kerr space-time we can let $\mu$ be the Sagnac tube with tangent field $t^{a} = \xi^a|_{\mu} + \omega|_{\mu}\psi^a|_{\mu}$, where $\omega|_{\mu}$ is the ZAMO angular velocity evaluated on this Sagnac tube and $\xi^a|_{\mu},\psi^a|_{\mu}$ are the stationary and axial Killing fields of the stationary source also evaluated on this Sagnac tube, since $t^a$ is a Killing field on $\mu$.

Now if I'm not mistaken, even though eq. (3) of the paper is derived in the specific context of a Sagnac tube at rest with respect to the stationary source i.e. $t^a = \xi^a$, the derivation of eq. (3) itself holds just as well for any $t^a$ which is a time-like Killing field on $\mathcal{M}$ (not just on $\mu$!) because from eq. (3) we have

$(\lambda_{M})^{1/2}\int _{\Sigma}\lambda^{-3/2}\omega^{a}\epsilon_{abc}dS^{bc}= (\lambda_{M})^{1/2}\int _{\Sigma}\lambda^{-2}\epsilon^{aefg}\epsilon_{abcd}t^dt_{e}\nabla_{f}t_{g}dS^{bc}= -6(\lambda_{M})^{1/2}\int _{\Sigma}\lambda^{-2}t^dt_{[b}\nabla_{c}t_{d]}dS^{bc}$

and furthermore $3t_{[b}\nabla_{c}t_{d]} = t_b t^d \nabla_c t_d - t_c t^d\nabla_b t_d -\lambda \nabla_b t_c = t_{[b}\nabla_{c]}\lambda - \lambda \nabla_{[b}t_{c]}$

hence $(\lambda_{M})^{1/2}\int _{\Sigma}\lambda^{-3/2}\omega^{a}\epsilon_{abc}dS^{bc}= 2(\lambda_{M})^{1/2}\int _{\Sigma}\nabla_{[a}(\lambda^{-1}t_{b]})dS^{ab} = \Delta \tau$.

Note that directly under eq. (3) in the paper, the authors state that the $\nabla_a$ appearing in the Sagnac shift is the derivative operator on $\mathcal{M}$ itself, and not just the derivative operator $\tilde{\nabla}_a$ on $\mu$. Hence the reason we need $t^a$ to be a Killing field on all of $\mathcal{M}$ and not just on $\mu$ is in the above calculation we needed to make use of $\nabla_{[a} t_{b]} = \nabla_a t_b$ under $\nabla_a$ and not under $\tilde{\nabla}_a$. This implies then that eq. (3) holds in Kerr space-time for the Sagnac tube given by the time-like Killing field $t^a = \xi^a + \omega\psi^a$ on $\mathcal{M}$, where as usual $\omega$ is a single ZAMO angular velocity held constant throughout space-time (note however that eq. (3) fails to hold for the ZAMO congruence for the aforementioned reason).

This brings me (finally!) to my question. We know that $\omega^a = \epsilon^{abcd}t_b \nabla_c t_d \neq 0$ for the above $t^a$. On the other hand we know from Malament's text that $\Delta \tau = 0$ should hold for this Sagnac tube since $L = t_a \psi^a = 0$ on $\mu$. This would require then that $\int _{\Sigma}\lambda^{-3/2}\omega^{a}\epsilon_{abc}dS^{bc} = 0$ for said Sagnac tube. I haven't yet attempted to show this explicitly by means of calculation but regardless, assuming I haven't made any mistakes above , is there a physically intuitive way to see why the above integral would necessarily have to vanish, even with $\omega^a \neq 0$? Do the symmetries of $\Sigma$ (see fig. 1) somehow make the flux of $\lambda^{-3/2}\omega^{a}$ through the Sagnac tube cancel out upon integration?

Thanks in advance.

 

[WannabeNewton]

Okay so if we take eq. (1) in the paper, for the above ZAMO Sagnac tube $\mu$ with tangent field $t^a = \xi^a + \omega|_{\mu}\psi^a$, and evaluate it along a curve $dt = d\theta = dr = 0$ on $\mu$, then $dS^a = \sqrt{g_{\phi\phi}}d\phi \psi^a$ and so $t_a dS^a \propto t_a \psi^a = L = 0$ hence $\oint_{S} \lambda^{-1}t_a dS^a = 0$ trivially which would then imply, as per Stokes' theorem as usual, that $\Delta \tau = \int _{\Sigma}\lambda^{-3/2}\omega^{a}\epsilon_{abc}dS^{bc} = 0$ but I still cannot see intuitively and physically why $\int _{\Sigma}\lambda^{-3/2}\omega^{a}\epsilon_{abc}dS^{bc} = 0$ directly without appealing to eq. (1) and Stokes' theorem; does anyone know of such a physically intuitive argument?

 

[WannabeNewton]

As an aside, I finished reading another paper that you guys might be interested in as it also deals with criteria of non-rotation, particularly a maximal acceleration criterion for non-rotation that we haven't discussed as of yet in this thread, and many of the calculations parallel what we have already calculated and discussed in this thread.

http://arxiv.org/pdf/gr-qc/9706029v2.pdf