I Preloading Pulleys: Understanding the Effects of Tension on Angular Velocity

[PaulB]

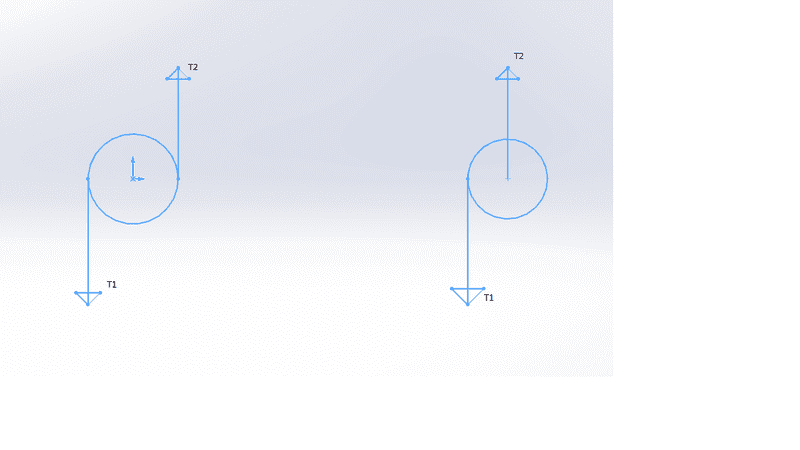
I am making a system Where I am pulling on opposite ends of a pulley with Tensions T1 and T2. Is this equivalent to preloading the pulley with tension T2? If I preload the pulley with T2 on a separate rope, how will the angular velocity change when I apply T1? I've drawn a quick diagram

 

[russ_watters]

Neither of these scenarios look much like a "pulley" to me - they look like spools. Neither are stable/in equilibrium. Are they free-floating in space? I don't see how you can "pre-load" something that isn't fixed. Anyway, no, the two scenarios are not equivalent: the torques applied to the spool are different.

 

[PaulB]

Neither of these scenarios look much like a "pulley" to me - they look like spools. Neither are stable/in equilibrium. Are they free-floating in space? I don't see how you can "pre-load" something that isn't fixed. Anyway, no, the two scenarios are not equivalent: the torques applied to the spool are different.

Hi Russ, you are correct. These are better described as spools fixed in space, but free to rotate around the point at the center of the circle. Let's say that they are bearings, sitting on shaft. In the left picture, the tension on T1 will simply be T1-T2. What will the tension on T1 be in the picture on the right.

 

[russ_watters]

Hi Russ, you are correct. These are better described as spools fixed in space, but free to rotate around the point at the center of the circle. Let's say that they are bearings, sitting on shaft.

In that case, there's an additional force missing from the pictures, one that acts at the center and opposes the net force of the applied T1 and T2.

In the left picture, the tension on T1 will simply be T1-T2. What will the tension on T1 be in the picture on the right.

I think you tripped over your wording there. I think you mean to ask about the force on the center bearing? T1 and T2 are applied forces, right? The force applied by the bearing is T1-T2, yes. For the second one, it's the same as long as T2 is somehow applied to the spool and not the fixt point directly. Otherwise T2 isn't really doing anything.