Principle of Virtual Work and static equilibrium

[Nytik]

Homework Statement

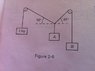
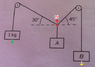
The system shown in Fig. 2-6 is in static equilibrium. Use the principle of virtual work to find the weights A and B. Neglect the weight of the strings and the friction in the pulleys.

Homework Equations

Conservation of gravitational potential energy.

The Attempt at a Solution

The system is in static equilibrium so the weights may be moved without changing the energy of the system. Consider weight A moving down by 1m (lets pretend this is a 'small distance' for the purposes of virtual work). Then by some geometry we find the 1kg weight moves up by \frac{1}{sin(30)} m and weight B moves by \frac{1}{sin(45)} m. By equating GPE,
A = \frac{1}{sin(30)} + \frac{B}{sin(45)}

For two unknowns we need two equations, but moving the other weights an amount just gives back the same one. I am unsure how to create a second equation.

Note: This problem is simple enough using forces but that is not the method asked for and I would like to improve my ability at using this method.

Thanks for your help!

 

[haruspex]

Your geometric calculations are wrong.
If A moves straight down at some speed, v, that pulls on the left hand string to the extent that its movement is along the direction of the string. I.e. the rate at which it will pull the string over the pulley is the component of v that lies in that direction. This will be less than v, not more.

 

[Nytik]

Hi, I don't quite understand that. First I should note there are no velocities involved here, we are considering two static states in one of which A is 1m further down than in the diagram. But for this to be the case, more than 1m of string should come over the pulley as the string is at an angle to the vertical. So the 1kg and B blocks will be more than 1m above their original positions. Where is the flaw in this?

 

[Dr.D]

Velocities of possible motion are often useful for discussion in virtual work problems.

For some displacement x(q), note that

delta x = dx/dq delta q
= dx/dt dt/dq delta q
= dx/dt // (dq/dt) delta q

The right side looks like the ratio of two velocities multiplying delta q

 

[vela]

From what I've read, the idea is to use a virtual displacement so that all but one unknown disappears. For example, hold B fixed and let the 45-degree angle increase by a small angle $\delta\theta$. You should find that the change in horizontal position of A is $\delta x = l_2 \delta \theta \sin 45^\circ$ and the change in vertical position of A is $\delta y = l_2 \delta \theta \cos 45^\circ$, where $l_2$ is the length of the string from A to the pulley on the right. Then you can find the change in $l_1$, the length of string from A to the pulley on the left, in terms of $\delta \theta$, and so on.

 

[haruspex]

From what I've read, the idea is to use a virtual displacement so that all but one unknown disappears. For example, hold B fixed and let the 45-degree angle increase by a small angle $\delta\theta$. You should find that the change in horizontal position of A is $\delta x = l_2 \delta \theta \sin 45^\circ$ and the change in vertical position of A is $\delta y = l_2 \delta \theta \cos 45^\circ$, where $l_2$ is the length of the string from A to the pulley on the right. Then you can find the change in $l_1$, the length of string from A to the pulley on the left, in terms of $\delta \theta$, and so on.

It is an interesting question as to what small displacements need to be considered. The OP appeared to be considering a vertical change in the position of A, so I followed suit. It does seem the simplest for the full calculation. But maybe some other direction of movement would lead to a different conclusion. So perhaps need to allow for a displacement in an arbitrary direction.
Nytik, if you consider A moving (down, say) at speed u instantaneously then in time dt it will move u.dt. You can use components of velocities to find how far other items move in time dt. It works the same just considering small displacement vectors, but it is perhaps more familiar to think in terms of components of velocities than components of displacements.

 

[OldEngr63]

This is one tough problem when attacked by virtual work!

I'm surprise to see this in an introductory physics course.

 

[Nytik]

Technically not an introductory physics course, this is just a question from the "Exercises for the Feynman Lectures on Physics". The question doesn't really fit any other forum though as far as I can tell.

Thanks for your help everyone, I should be able to reach a solution from here.

 

[Dr.D]

Be sure t heck your result by simplefrce summations equal to zero, This is the best way to be sure your analysis is correct.

 

[TSny]

To me it seems simplest to consider displacing the knot where the three strings meet. If you consider a vertical virtual displacement of the knot by $\small \delta y$ (as shown) , then it is not hard to deduce the corresponding vertical displacements of the three masses in terms of $\small \delta y$. The net work done by gravity for these displacements must be zero. Repeat for a horizontal virtual displacement of the knot.

 

[Dr.D]

The essential point to recognize first is that four values are required to describe the system configuration (y1, xa, ya, yb), and there are two constraints (length of the cord from m1 to ma = const, length of cord from ma to mb = const). Thus, 4 - 2 = 2 dof. Then you can choose which coordinates to call independent at will. The choice suggested by the previous poster is a good choice.

 

[OldEngr63]

The comment from TSny is essentially correct, but it misses one of the finer points.

If simultaneous virtual displacements of the central knot are made (delta-xa, delta-ya), then the virtual work resulting from the combination will involve an expression of the form
delta-W = delta-xa (...) + delta-ya( ...) = 0
If delta-xa and delta-ya are independent, then the only way to assure the vanishing of the virtual work is for the coefficient of each variation to vanish independently. This gives the necessary two equations to be solved for the unknown masses.