physicsissohard
- 19
- 1
- Homework Statement
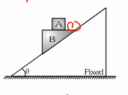
- Block a of mass m is placed over a wedge of the same mass m. Both the block and wedge are placed on a fixed inclined plane. assuming all surfaces to be smooth calculate the displacement of block in ground frame in 1 s
- Relevant Equations
- the homework question.
This is what I thought. since the y component of both their accelerations will be same. we can do this. Mg-N=ma where N is the normal force. and for the wedge it is N+Mgsin^2(theta)=ma using second law of motion where N is the normal force. sin^2(theta) because i resolved gravity twice. now if you elminate N from the equation you get g(1+sin^2(theta))/2 and if you put it in the law of kinematics with t=1 it becomes g(1+sin^2(theta))/4. But apparently thats not the correct answer and I have no idea why.