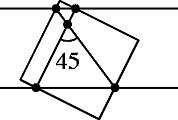
We may as well take $a=1$. Tilt the diagram so that the square becomes the unit square, and suppose that the parallel lines make an angle $\theta$ with the $x$-axis.
[TIKZ][scale=1.25]
\draw [very thick] (0,0) -- (4,0) -- (4,4) -- (0,4) -- cycle ;
\draw [very thick] (-4,0.5) -- (4,6.5) ;
\draw [very thick] (0,-1.5) -- (8,4.5) ;
\coordinate [label=left:$A$] (A) at (0,3.5) ;
\coordinate [label=above:$B$] (B) at (0.667,4) ;
\coordinate [label=right:$C$] (C) at (4,1.5) ;
\coordinate [label=below:$D$] (D) at (2,0) ;
\draw [very thick] (A) -- (C) ;
\draw [very thick] (B) -- (D) ;
\draw (2.5,0.2) node {$\theta$} ;
\draw (1.3,2.6) node {$\phi$} ;
\draw (-0.5,0) node {$(0,0)$} ;
\draw (4.5,0) node {$(1,0)$} ;
\draw (-0.5,4) node {$(0,1)$} ;
\draw (4.5,4) node {$(1,1)$} ; [/TIKZ]
The equations of the parallel lines are then of the form $y = x\tan\theta + c+d$ and $y = x\tan\theta + c-d$ for some constants $c$ and $d$. The condition that the lines form a strip of width $1$ is $2d\cos\theta = 1$. So $2d = \sec\theta$.
The points where the lines cross the sides of the square are then $$ A = (0,c+d),\qquad B = ((1-c-d)\cot\theta,1), \qquad C = (1,\tan\theta + c-d), \qquad D = ((d-c)\cot\theta,0) .$$ The slope of the line $AC$ is therefore $\tan\theta - 2d = \tan\theta - \sec\theta$.
The slope of $BD$ is $\dfrac{-1}{(2d-1)\cot\theta} = \dfrac{-\tan\theta}{\sec\theta-1}$.
It follows from the formula $\tan(\alpha - \beta) = \frac{\tan\alpha -\tan\beta}{1+ \tan\alpha\tan\beta}$ that if $\phi$ is the angle between $AC$ and $BD$ then $$\begin{aligned} \tan\phi = \frac{(\tan\theta - \sec\theta) - \frac{-\tan\theta}{\sec\theta-1}}{1 + (\tan\theta - \sec\theta) \frac{-\tan\theta}{\sec\theta-1}} &= \frac{(\sec\theta - 1)(\tan\theta - \sec\theta) + \tan\theta}{(\sec\theta - 1) - \tan\theta (\tan\theta - \sec\theta)} \\ &= \frac{\sec\theta(\tan\theta - \sec\theta + 1)}{\sec\theta(1 - \sec\theta + \tan\theta)} \\ &= 1. \end{aligned}$$ It follows that $\phi = 45^\circ$.
 protrude beyond a strip of width
protrude beyond a strip of width
 with parallel edges. The sides of the square intersect the edges of the strip at four points. Prove that the diagonals of the quadrilateral whose vertices are these points intersect at an angle of
with parallel edges. The sides of the square intersect the edges of the strip at four points. Prove that the diagonals of the quadrilateral whose vertices are these points intersect at an angle of
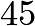 degrees.
degrees.